Simulation zufälliger Stöße einer Strömung

Zur Beurteilung, ob überhaupt in einem Gas harter Kugeln zufällige Strukturbildungen und deren längerer Erhalt möglich sind, soll vorab untersucht werden, ob bei gewissen einfachen Strömungen, die aber noch ortsfrei beschrieben werden sollen, massenweise Geschwindigkeitsbetragsänderungen und bevorzugte Richtungen auftreten können. Als weiteste derzeit geplante Simulation des ortslosen HKG´s, werden die weiter unten versuchten einseitigen Stöße so betrachtet, als ob ein existierendes System eine Seite des umgebenden Normalraums abschirmt. Das wird hier zuerst durch Beschränkung der zulässigen Winkel erreicht. Der aktuelle Stand der Überlegungen zum Harte Kugel Modell soll hiermit ergänzt werden.
Die Definitionen und einige weitergehende Überlegungen sind in Bearbeitung, aber auch unter http://uratom.de/Beweise/Definitionen.htm zu finden. Wesentliche Merkmale müssen wegen der Ortsfreiheit aus der Stoßfrequenzraumwinkeldichte in Zufallsgeneratoren zur Erzeugung von Stoßpartnern übertragen werden.
Dieses gesamte Mathcad-Dokument lässt sich nun durch ein Skript viele Male starten.
Die Stoßtransformationen werden dabei wie in anderen vorgestellten Simulationsversuchen (.../Beweise ) verwendet. Zuerst wird die Relativgeschwindigkeit der Stoßpartner bestimmt:

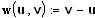
(1)

Die Richtung der Relativgeschwindigkeit wird mit der Kugelkoordinaten-Transformation ermittelt, für die hier die in Mathcad eingebaute Funktion verwendet wird:

(2)

(3)

Bei den Ergebnissen mit der ausführlichen Transformation gemäß dem Artikel über Kugelkoordinaten in Wikipedia, nimmt F Werte von 0 bis 2 p an.
Die Stoßachsenwinkel ergeben sich i.A. zufallsabhängig, wobei gleichwahrscheinliche parallele Bahnen zur Richtung der Relativgeschwindigkeit angenommen werden. Das ist auf gleichwahrscheinliche parallele Bahnen bei den Stoßpartnern zurückzuführen. Damit ergibt sich in kartesischen Koordinaten der Stoßachsenvektor:

(4)

Dieser wurde relativ zur Richtung der Relativgeschwindigkeit w(u,v) erzeugt und muss nun im ursprünglichen Koordinatensystem (dem Laborsystem von u und v) ausgedrückt werden, was durch zwei hintereinander ausgeführte Drehungen erreicht wird:

(5)

(6)

Damit ergibt sich die Stoßachse im ursprünglichen Koordinatensystem durch das zweifache Zurückdrehen zu:

(7)

Dieses S entspricht beim Zentralstoß auf eine ruhende Kugel dem ursprünglichen u bzw. beim Zentralstoß auf ein beliebiges v allgemeiner dem Relativgeschwindigkeitsvektor w normiert auf 1.

Beim Stoß werden nun die zur Stoßachse parallelen Geschwindigkeiten der beiden beteiligten Kugeln ausgetauscht. Alle Vektoren sollen jedoch weiterhin im ursprünglichen Koordinatensystem betrachtet werden.

(8)

parallele Geschwindigkeiten

(9)

(10)

orthogonale Geschwindigkeiten

(11)

(12)

Geschwindigkeiten nach Stoß

(13)

Für die Simulation von Stößen (ortsloses Gas) werden jetzt die bereits gespeicherten Daten für z Stöße verwendet, um z weitere Stöße damit zu erzeugen:

(für die interne Durchlaufzählung)

(14)

(15)

Die Zahl der Durchläufe und damit Stöße ist demnach hier

Für

(16)

werden die alten Geschwindigkeitsvektoren u_s als neue u verwendet. Die gesamte Menge der z = 10000 Teilchen wird so durch neue zufällige Stöße aus der Umgebung bei jedem Durchlauf verändert.

(17)

Die Geschwindigkeitsbeträge der u, die für die neuen Stöße verwendet werden sollen, ergeben sich aus den alten gespeicherten (ortslosen) Gas:

(18)

Mit dem Zufallsgenerator für die Maxwellsche Geschwindigkeitsverteilung werden bei jedem Programmdurchlauf des gesamten Dokuments neue zufällige v erzeugt, die demnach die Durchschnittsgeschwindigkeit 1 besitzen:

(19)

(20)

(21)

(22)

(23)

(24)

Neben den Geschwindigkeitsbeträgen wird nun ein zufälliger Winkel für den Stoßpartner (Flugwinkel = Bahnenwinkel) benötigt, weil diese Winkel in Abhängigkeit von den Eigenschaften einer viel größeren Anzahl von Kugeln und deren Stoßfrequenzraumwinkeldichte betrachtet werden sollen. Dafür wird eine zufällige Verteilung verwendet, wobei angenommen wird, dass u in z-Richtung liegt. Die Stoßfrequenz sei nun proportional zur Relativgeschwindigkeit und dieser Wert wird entsprechend der Stoßfrequenzraumwinkeldichte (3-dimensional) korrigiert. Auf der Kugeloberfläche kommen die Winkel Richtung Pol seltener vor, weil die Kreise des unabhängig von b erzeugten Winkels F kleiner werden, deshalb kommt zum Relativgeschwindigkeitsbetrag der Faktor sin(b) hinzu:

(25)

Natürlich ergibt sich mit dieser Verteilungsfunktion

Sie wird nun im zu konstruierenden Zufallsgenerator verwendet, wobei der Gedanke zugrunde liegt, dass die zufälligen gesuchten Winkel gemäß dieser Verteilung durch Einsetzen eines gleichmäßig verteilten zufälligen Wertes 0 < y < 1 erzeugt werden kann:

(26)

Zur Nullstellenbestimmung wird die Lösungsmenge mit einer Näherungslösung aus dem zulässigen Intervall initiiert. 0<y<1 ist der zufällige Funktionswert des Zufallsgenerators.

(27)

(28)

sowie dann die root-Funktion verwendet:

(29)

Außerdem muss noch F der Drehwinkel des Vektors v um die Richtung von u zufällig bestimmt werden. Das geht wie für den Winkel f:

(30)

Außerdem werden neue Stoßachsenwinkel generiert, bei denen f und q auf der Annahme gleichwahrscheinlicher paralleler Bahnen beruhen und die stoßenden Vektoren aus der beobachteten Menge und der zufälligen Umgebung bestimmt. Für den eigentlichen Stoß mit den obigen Stoßtransformationen werden die ursprünglichen z = 10000 u aus der gespeicherten Datei PSI verwendet.

(31)

(32)

z.B.:

(33)

(34)

Hier wird u in z-Richtung angenommen und v nimmt bei seiner zufälligen Erzeugung Bezug darauf. Weil das Stoßgebilde im Moment der Berührung aus zwei fest zueinander ausgerichteten Vektoren besteht, muss v noch ins ursprüngliche Koordinatensystem gedreht werden. In Kugelkoordinaten werden die U zu B und deren Drehwinkel sind:

(35)

(36)

Das Zurückdrehen der zufällig erzeugten Vektoren V erfolgt nun durch die Matrizen mit den Winkeln q und f:

(37)

(38)

Mit diesen ergibt sich durch die Drehung:

(39)

z

Erst um z-Achse drehen, so dass x-Achse sich mit r_0 deckt, dann um neue y-Achse. Um diese Werte müssen alle Vektoren zurück gedreht werden. Der x'-Wert ist die senkrechte Projektion und diese wird 0.
(aus Wikipedia: .../Kugelkoordinaten)

y

x

Damit ergeben sich nach dem Stoß die beiden Geschwindigkeitsvektoren:

(40)

(41)

Diese sollen wieder für weitere Untersuchungen im ursprünglichen Koordinatensystem ausgedrückt werden.

Zur bequemeren Speicherung für eine spätere Auswertung nach vielen Stößen werden die Parameter nach dem Stoß wieder zum gleichen Gebilde zusammengefasst.

Damit ergibt sich die 8 mal 10000 Stellen umfassende Matrix:

(42)

aus welcher eindeutig die ursprünglichen Vektoren vor dem Stoß rekonstruiert werden können. Diese wird gespeichert.

Außerdem werden nur zur direkten Überwachung der Durchläufe einige Kennzahlen ermittelt

Intern für das Durchlaufssteuerungsscript ergibt sich:

(43)

(44)

(45)

(46)

(47)

(48)

Der Geschwindigkeitsmittelwert aller Kugeln nach den Stößen ist demnach

(49)

(50)

Davon soll die Entwicklung bei vielen Programmdurchläufen gespeichert werden:

(51)

Für einfache alte Auswertungen wird die Datei auch noch in alter Form gespeichert:

(52)

Grafisch ergeben sich für die Verteilung der Flugwinkel die folgenden Werte:

(53)

(54)

Die Parameterentwicklung kann auch grafisch dargestellt werden:

(55)

(56)

(57)

(58)

(59)

(60)

Die Durchlaufzahl gibt nur an, wie viele male das ganze Dokument neu berechnet wurde. Der Mittelwert der betrachteten Geschwindigkeitsbeträge nähert sich schnell 0.8 und auch die Varianz wird kleiner. Nötig wäre aber eine Betrachtung der Ortszeitentwicklung.