Struktur und Dynamik der Materie im

4.2 Geschwindigkeiten, Winkel und Dichte in gegenseitiger Abhängigkeit

Durch algebraische Verknüpfungen lassen sich bekanntlich aus den elementaren Kovariantengebilden neue Ausdrücke konstruieren. Wird die Selbstwechselwirkung außer Betracht gelassen, gelten somit die Symmetrien und Erhaltungssätze der modernen Physik (Noether-Theorie). Die Selbstwechselwirkung kann aber immer auf einen Zweierstoß zurückgeführt werden. Aus der Stoßformel folgt nun durch einfaches Einsetzen

Da im ursprünglichen sowie im gestrichenen System (neuem) auch die Annäherungs- und Entfernungsgeschwindigkeitsbeträge übereinstimmen, gilt dies ebenfalls für die daraus bildbaren Quadrate. Durch Induktionsbeweis lässt sich damit zeigen, dass auch in der Grundmenge mit Selbstwechselwirkung Impuls- und Energieerhaltungssatz gemäß der natürlichen Vorstellung gelten.

Das darf aber nicht darüber hinweg täuschen, dass bei den Zusammenstößen im allgemeinen die Summen und Differenzen der Beträge der Einzelgeschwindigkeiten verändert werden, was bei einem rechtwinkligen Zusammenstoß, bei dem eine Kugel praktisch zur Ruhe gebracht werden kann und die resultierende Geschwindigkeit der anderen nach dem Satz von Pythagoras nur den Betrag der Hypotenuse erhält, am leichtesten einzusehen ist. Durch diese Veränderungen werden Systembildungen erst denkbar, wenn sich die unterschiedlichen Komponenten massenweise in verschiedenen, zusammengehörenden Teilmengen der Grundmenge, d.h. Systemen befinden.

Elementare Eigenschaften der Grundmenge sind die Anwesenheit und die Bewegung der Uratome an Raum-Zeit-Punkten. Wegen der notwendigen Wahrscheinlichkeitsbetrachtung wird angenommen, dass diese durch die Dichte- und Geschwindigkeitsverteilung genügend genau beschrieben werden können.. Welchen Einfluss haben aber nun die möglichen Vektorwinkel und vielleicht die Stoßachsenwinkel auf diese Wahrscheinlichkeitsverteilungen?

Freie Weglänge und Stoßhäufigkeit:

In der Ausgangssituation soll vorerst ein Medium betrachtet werden, bei dem die Anzahldichte gleich verteilt und die vorkommenden Geschwindigkeiten normal verteilt sind. Die Wahrscheinlichkeitsdichten ergeben sich dabei nach den geometrischen Grundüberlegungen der Wahrscheinlichkeitsrechnung und führen zu den bekannten Maxwellschen Verteilungsfunktionen. Außerdem sei ein festes Koordinatensystem so gewählt, dass die räumlichen Koordinaten und die Zeit reell sind und orthogonal zueinander stehen. Die x- oder 1-Achse liege in der Richtung einer willkürlich ausgewählten Probekugel, welche sich gerade mit Durchschnittsgeschwindigkeit in positiver Richtung bewegt. Ihr Durchmesser sei 2 d ,weil damit alle für einen Stoß in Frage kommenden Kugeln als Punkte angesehen werden können. Die Anfangsorte der Probekugel liegen in einem Zylinder mit gleicher Wahrscheinlichkeit an jedem Ort und die aller durch Punkte dargestellten Kugeln demnach in einem Volumen, welches nur durch die maximale Geschwindigkeit beschränkt ist und das vom Anzahldichte- Erwartungswert bestimmt wird. Der Einfachheit halber wird hier der Zusammenhang verwendet, dass die durchschnittliche freie Weglänge L mit der Anzahldichte n und dem Durchmesser d folgendermaßen bestimmt ist:

Dieser Zusammenhang entsteht durch eine gedachte Verschiebung aller Kugeln in eine voll aufgefüllte Ebene wie in der kinetischen Gastheorie. Damit gilt dann für die absolute Zusammenstoßhäufigkeit:

Vektorwinkel:

(NEUERE ANMERKUNG: Mittlerweile hat sich herausgestellt, dass es günstiger ist, die vorkommenden Winkel von der Stoßfrequenz her abzuleiten. Vgl. dazu B-stoss.pdf und Betavert.htm)

Wie bei den Anfangsorten gibt es nun kein Argument für die Annahme der Auszeichnung irgendwelcher Raumrichtungen. Zum Zusammenstoß können aber nur die Punkte gelangen, welche die Bahn unserer Probekugel, also den Stoßzylinder, kreuzen. Diese können durch zwei reelle Größen, nämlich den Öffnungswinkel ß und den Geschwindigkeitsbetrag |v| beschrieben werden, weil das Koordinatensystem um die x-Achse so gedreht werden kann, dass der zweite mögliche Raumwinkel wegfällt. Die Mehrzahl aller Punkte aus dem betrachteten Raumgebiet bewegt sich in Richtungen, welche nicht zu einem Stoß mit der Probekugel führen können. Diesen wird der Weg 0 im Stoßzylinder zugeordnet und somit fallen sie vorerst aus der Betrachtung heraus. Für die Ermittlung der Stoßwahrscheinlichkeit, bzw. zuerst der entsprechenden relativen Häufigkeit der Durchquerung des Bereichs der zufälligen Anwesenheit der Probekugel, liegt der entscheidende Gedanke zugrunde, dass diese von der Aufenthaltszeit t der bewegten Punkte in einem solchen Bereich abhängen muss. Nach einfacher geometrischer Überlegung muss diese direkt vom Weg

s = 2 d / sin ß

der Punkte im Stoßzylinder bestimmt werden. Bei gleichzeitiger Berücksichtigung der Anzahl für einen Stoß in Frage kommender Punkte, d.h. der Anzahldichte, besteht offenbar der Zusammenhang, dass bei kleiner Geschwindigkeit die Aufenthaltszeit im Stoßbereich zwar groß wird, dafür aber nur ein kleines Volumen aus dem die Punkte kommen können, zur Verfügung steht. Daher könnte die Geschwindigkeitsabhängigkeit bei dieser einfachen Betrachtung wegfallen, wenn nur angenommen wird, dass jeder Ort im L langen Stoßzylinder gleich wahrscheinlich ist und die gesuchte Zeit wird deshalb proportional zum darin zurückgelegten Weg s .

Die relative Häufigkeit bzw. Wahrscheinlichkeit für das Vorkommen gewisser Winkelbereiche ergibt sich jetzt aus dem Verhältnis der Summen, bzw. hier wegen der Unkenntnis einzelner Vektoren, der Integrale aller interessierenden zu allen möglichen Aufenthaltszeiten, d.h. im Stoßzylinder zurückgelegten Wege, in Abhängigkeit von den Vektorwinkeln (Öffnungswinkel) welche aus Symmetriegründen auf p /2 beschränkt sind. Ansonsten müsste die folgende Betrachtung mit den adäquaten Streuungen erfolgen. Gesucht ist demnach der Erwartungswert des Vektorwinkel(betrag)s in Abhängigkeit von der freien Weglänge, weil vorerst nur ein Zusammenstoß betrachtet wird. Die Anzahldichteabhängigkeit ist somit bereits eingeschlossen, während die Geschwindigkeitsabhängigkeit erst bei vielen Stößen interessant wird. Aus Vollständigkeitsgründen wird aber hier die in Bewegungsrichtung liegende (Relativ-) Geschwindigkeitskomponente v_{_}mitgeschrieben.

Es ergibt sich also bei Annahme der Begrenzung durch die durchschnittliche freie Weglänge L, mit u= v₁ und v = v₂

     t_u = L / u
t_v(ß) = L / v_Þ                 für 0 < ß < 1 / L
           L / v_Þ sin b        für 1 / L <beta < p / 2
           0 sonst

Der gleichzeitige Aufenthalt in einem sicher zum Stoß führenden Bereich wird nun wahrscheinlichkeitstechnisch durch das Produkt zweier Wahrscheinlichkeitsdichten, welche mit t_uund t_v(ß) gebildet werden, ausgedrückt. Anstelle der Zeiten können aber auch die Wahrscheinlichkeitsdichten der Geschwindigkeiten selbst verwendet werden. Bei der Berechnung der Auftreffwahrscheinlichkeit muss dann das Doppelintegral über die Dichten gebildet werden. Ist nun viel Wahrscheinlichkeit um 1 konzentriert (kleine Streuung) und sind beide Geschwindigkeits-Erwartungswerte annähernd 1, ergibt sich:

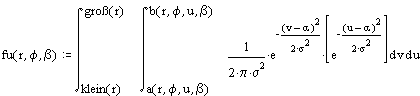
und die Abhängigkeit von der freien Weglänge L erscheint erst in den Integrationsgrenzen der Wahrscheinlichkeitsfunktion, wo sie allerdings wiederum zur Vereinfachung durch einen durchschnittlichen Abstand r ersetzt werden kann. Dort muss nämlich die wesentliche Nebenbedingung berücksichtigt werden, welche Geschwindigkeiten beim Ursprung der Bewegung von einem beliebigen Punkt aus nur das untersuchte Uratom treffen können. Dieser Bereich ergibt sich dadurch, dass die Relativgeschwindigkeit in einem auf die untersuchte Kugel zeigenden Kegel liegen muss.

Für a und b ergeben sich leider umfangreiche Ausdrücke, die aber mit Hilfe einer Skizze nachvollzogen werden können: (korrigiert in Betavert.htm)

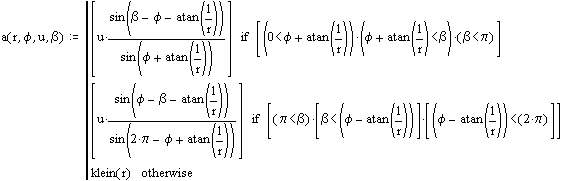
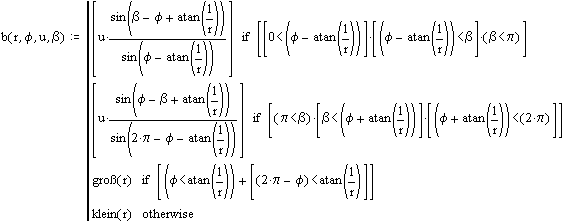
Die Relativgeschwindigkeit muss für einen Stoß auf einen Bereich mit doppeltem Uratom- Durchmesser zeigen. Dadurch können einfache Raumpunkte untersucht werden. Durch geschickte Wahl der Zeiteinheit entsprechen die Wege den Pfeillängen der Geschwindigkeiten.

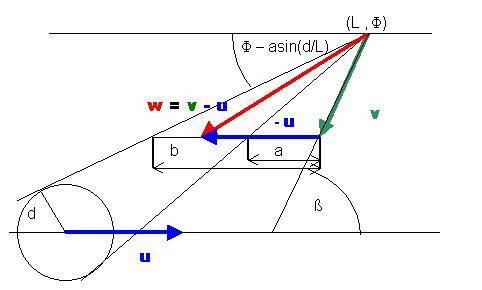
Stoßkegel

Im Prinzip kann v über alle Grenzen integriert werden, wegen der Anhäufung um den Erwartungswert der Geschwindigkeit versagt aber ein einfacheres Computer- Algebra- System bei der numerischen Berechnung obigen Doppelintegrals. Deshalb werden eine kleine und große Grenze so festgelegt, dass fast alle Wahrscheinlichkeit im Integrationsbereich liegt. Das ist bei kleinem L für viele Stoßwinkel ß der Fall.
Je größer aber L wird, desto schmaler wird der Stoßkegel und nur noch bei kleinem Stoßwinkel ß fällt ein großer Anteil der Endpunkte von Relativgeschwindigkeitsvektoren in diesen. Der Beweis erfolgt eigentlich durch Integration über den gesamten Raum, aus Symmetriegründen kann die Variablenzahl aber verringert werden. Da bei größer werdendem Parameter L (hier also r ) und kleiner werdender Streuung s die Wahrscheinlichkeit, also die Fläche unter fu (r,phi,ß),, d.h. die Anzahl der von einem Punkt aus zum Stoß führenden Uratome, kleiner wird und sich immer näher zu kleinerem ß verlagert, ist eine Beweisidee gefunden. Die folgende Grafik ist ein typisches Beispiel, das bei allen abnehmenden Streuungen und zunehmenden freien Weglängen (hier r) noch extremer wird:

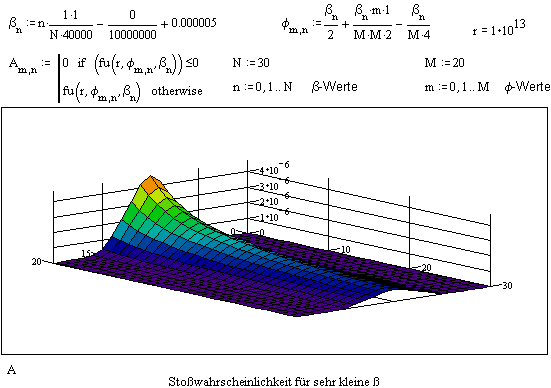
Wegen der aus der kinetischen Gastheorie bekannten Formel d / L = sqrt (2) pi n d³ wird hieraus der wichtige Zusammenhang mit der Dichte deutlich. Es folgt demnach, dass in einem dünnen Medium, d.h. bei großer freier Weglänge im Verhältnis zum Kugeldurchmesser, viel mehr kleine Vektorwinkel auftreten, als alle anderen. Das heißt mit anderen Worten, dass orthogonale Komponenten zur Relativgeschwindigkeit bei Zusammenstößen im dünnen Medium fast verschwinden. In einem dünnen Medium sind Frontalstöße häufiger als Querstöße. Das ist eine wesentliche Symmetrie im Normalraum, welche aber durch mögliche Anhäufungen gebrochen werden kann. (vgl. aber auch Einwände in Beweise,...)

Stoßachsenwinkel:

Der Stoßachsenwinkel a (jetzt q ) ist eigentlich eine Größe im einmal gewählten räumlichen Koordinatensystem. Da aber vorn eine sich bewegende Probekugel ausgezeichnet wurde, lag das Koordinatensystem mit einer Achse in der Bewegungsrichtung. Hier hat gemäß einfacher wohlbekannter geometrischer Überlegungen nur die Relativgeschwindigkeitsrichtung einen Einfluss auf a.

In allen weiteren Überlegungen wird angenommen, dass parallele Bahnen gleich wahrscheinlich sind. Die zufällige Erzeugung erfolgt deshalb für eine Winkelkomponente mit rnd(2 p), für die andere mit asin(sqrt(rnd(1)).

Auftretende Geschwindigkeiten:

Unberücksichtigt sind bisher unterschiedliche Geschwindigkeiten der Stoßpartner und die eigentliche Wechselwirkung durch den Stoß. Aus Symmetriegründen erfolgt wieder die Beschränkung auf eine Ebene.

Sind anfangs alle Geschwindigkeiten gleich, so werden durch die vorkommenden Querstöße, bei denen zusätzlich im allgemeinen verschiedene Stoßachsenwinkel auftreten, ständig neue Geschwindigkeitsbeträge produziert. Seien ß der Vektorwinkel, a der Stoßachsenwinkel u bzw. v die Geschwindigkeitsbeträge vor dem Stoß. Dann gilt für die Geschwindigkeitsbeträge nach dem Stoß nach Pythagoras und der Voraussetzung, dass nur die Geschwindigkeiten parallel zur Stoßachse ausgetauscht werden:

u´ = | sqrt(u² sin² (ß-a ) + v²cos²a)|

v´ = | sqrt (v²sin² a + u² cos² (ß -a ))|

Da sin² (pi + ß - a ) = sin²(ß -a) und cos² (pi + ß - a) = cos²(ß -a) sind, wurde pi weggelassen. Mit einfachen Zahlenbeispielen wird daraus offensichtlich, dass meistens unterschiedliche Geschwindigkeitsbeträge erzeugt werden, welche keine Symmetrien erkennen lassen, falls der Vektorwinkel ß <> 0 ist. Bei der Bildung von Geschwindigkeitsbetragssummen vor und nach dem Stoß lässt sich der Verlauf der Änderungs- bzw. Differenzfunktion

f (a,ß,u,v) = (u + v) - (u´ +v´)

mit verschiedenen, aber festen, Geschwindigkeitsbeträgen und Stoßachsenwinkeln untersuchen. Bei ß ungefähr = 0 , was in dem untersuchten dünnen Medium als häufiger Zusammenstoßfall möglicherweise angenommen werden kann, vereinfachen sich die Formeln auf:

u´ = | sqrt(u² sin² (-a ) + v² cos²a) |

v´ = | sqrt (v²sin² a + u² cos² ( -a ))|

Trotz gleichbleibendem Relativgeschwindigkeitsbetrag nach einem beliebigen Stoß, folgt hieraus die wesentliche Erkenntnis, dass in einem einmal gewählten Koordinatensystem die Geschwindigkeitsbetragsdifferenz der beiden Stoßpartner nach dem Stoß in der Mehrzahl aller möglichen Stöße kleiner ist als vorher. Bei einem durchschnittlichen Stoßachsenwinkel a = 45° ist es sogar gleichgültig, welche Geschwindigkeitsbeträge die beiden Kugeln vor dem Stoß hatten, nach dem Stoß sind sie exakt gleich.

Interessanterweise gilt auch, dass die Betragssumme nach dem Stoß meistens größer wird, was anhand einfacher Skizzen oder eines kleinen Simulationsprogrammes leicht verständlich wird. Unter Variation von a ergibt sich beispielsweise bei kleinem ß (Frontalstößen) meistens ein negativer Verlauf, was ein Zeichen für Geschwindigkeitsausgleich ist:

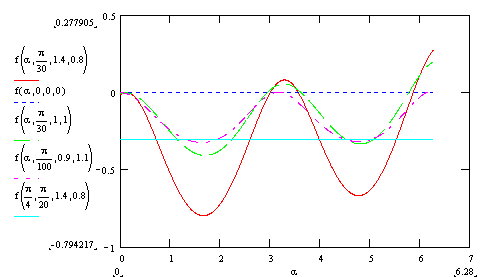
Bei bereits gleichen Geschwindigkeitsbeträgen in dem festen Koordinatensystem, vor einem Frontalstoß mit beliebiger Stoßachse, bleiben die Geschwindigkeitsbeträge nachdem Stoß unverändert. Später werden wir auch sehen, dass bei großem ß, die betrachteten Kurven auch im Positiven verlaufen können.

Aus diesen Überlegungen folgt, dass bei einer hohen Frontalstoßhäufigkeit und nach dem Gesetz der großen Zahlen, eine sehr schmale Kurve der Geschwindigkeitsverteilungsdichte erzeugt werden kann. Die kleine Streuung ist auf die trotz allem stattfindenden nicht frontalen Stöße zurückzuführen. Durch den Geschwindigkeitsanpassungsprozeß gleichen sich die von der Durchschnittsgeschwindigkeit abweichenden Geschwindigkeiten dieser aber nach mehreren Stößen an.

Obwohl die schmale Geschwindigkeits-Normalverteilung bei Frontalstößen auftritt, sind aber Kugelmengenflüsse mit breiterer Geschwindigkeitsverteilung und von der Durchschnittsgeschwindigkeit abweichendem Erwartungswert möglich. Die absolute Zusammenstoßhäufigkeit

bestimmt den erwarteten Uratom-Fluss durch eine interessierende Fläche. Deshalb ist ein multiplikativer Zusammenhang mit den vorn betrachteten Wahrscheinlichkeiten für das Auftreten von Vektor- und Stoßachsenwinkeln denkbar. Bei einer entsprechenden Vektordarstellung lassen sich möglicherweise die Erwartungswerte direkt einsetzen. Eine exakte Untersuchung soll jedoch der vorgeschlagenen Elementarteilchentheorie vorbehalten bleiben. Etwas ausführlicher werden diese Gedanken aber auch später bei der Diskussion der Elementarteilchen und Wechselwirkungen behandelt.

Wichtig ist hier der schon verwendete Zusammenhang, dass die Stoßhäufigkeit von der erwarteten Aufenthaltszeit in einem bestimmten Raumbereich abhängt. Diese ist zwar umgekehrt proportional zur (Relativ-)Geschwindigkeit der betrachteten Kugeln, die Stoßzahl Z erhöht sich aber proportional zu dieser. Die freie Weglänge ist dabei geschwindigkeitstunabhängig.
Für den Aufbau der Welt aus Uratomen wichtige Zusammenhänge zwischen den elementaren Eigenschaften einer Uratomansammlung und deren Stoßverhalten seien deshalb nochmals in Stichworten zusammengefasst:

- Die Geschwindigkeitssumme vor einem Stoß ist gleich der Summe nach dem Stoß.

- Der Geschwindigkeitsdifferenzbetrag vor einem Stoß ist gleich der Differenz nach dem Stoß.

- Die Geschwindigkeits-Betrags-Summe ist im dünnen Medium (nach einem Normalstoß) meistens größer als vorher.

- Die Geschwindigkeits- Betrags- Differenz ist nach einem Normalstoß meistens kleiner.

- Der Annäherungsgeschwindigkeits-Betrag ist gleich dem Entfernungsgeschwindigkeits-Betrag, auch nach einem Stoß.

- Das Geschwindigkeits-Betrags-Summen-Maximum ergibt sich bei ausgeglichenen Absolutgeschwindigkeiten vieler Stoßpartner.

- Das Geschwindigkeits-Betrags-Summen-Minimum ergibt sich bei unterschiedlichsten Absolutgeschwindigkeiten vieler Stoßpartner.

- Bei Frontalstößen ergibt sich ein Absolutgeschwindigkeits-Betrags- und Anzahldichte-Ausgleich.

- Bei Querstößen ergibt sich oft eine Absolutgeschwindigkeits-Betrags- und Anzahldichte-Unterschieds-Zunahme.
- Das normale Vakuum (Normalraum) ist möglicherweise ein sehr dünnes Medium mit vielen vorkommenden Frontalstößen, bei denen sich die Geschwindigkeiten an die Durchschnittsgeschwindigkeit anpassen.

- Nach einem Stoß, bei dem die Geschwindigkeits-Betrags-Summe kleiner wird, nimmt die Anzahldichte zu, weil nach einem festen Zeitintervall die Entfernungssumme vom Stoßpunkt kleiner ist als im gleichen Zeitintervall vor dem Stoß.

Stoßgebilde verzerren also die Raumzeit durch die Selbstwechselwirkung der elementaren Felder auch an anderen Orten, wo sich momentan kein Uratom befindet.Anschaulich vorstellbar wird das durch die mit jeder Bewegung verbundene Änderung der Auftreffwahrscheinlichkeit. Eine Beschreibung dieses "unendlichen" Einflusses auch entfernter Uratome erfordert wegen der prinzipiellen Unkenntnis exakter Werte von Ort und Geschwindigkeit leider komplizierte mathematische Methoden, wie die Verwendung von Hilberträumen, der Differentialgeometrie,...

Die Anzahldichtezunahme und damit selbständige Materieansammlung in einer chaotischen Menge stoßender Kugeln stehen im Widerspruch zur landläufigen Meinung und es ist unklar, ob darüber schon berichtet wurde?

Inhalt

Grafik

Links

Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)