Albert Lothar Wiese, Sarajevo und Porec 2007/2009
Definitionen für ein Gas idealer harter Kugeln
Die Idee und Motivation für eigene Untersuchungen, was in einem einfachen Gas idealer harter Kugeln (HKG) (das nicht mit einem idealen Gas verwechselt werden sollte) geschehen kann, gehen auf das zurück, was in http://uratom.de seit dem Jahr 2000 vorgestellt wurde. Dort zeigte sich, dass eindeutige Definitionen unumgänglich sind. Vor allem Lothar Brendel von der Uni Duisburg wies immer wieder darauf hin. Aus unterschiedlichen Quellen stammende Definitionen, die von einem mathematischen und physikalischen Autodidakten verwendet werden, sind eine riesige Fehlerquelle. Vor allem in umfangreichen alten Dokumenten ist eine nachträgliche Änderung kaum zu bewerkstelligen. Deshalb sollten hier für eine weitere Arbeit die wichtigsten Begriffe definiert werden, die aber auf Anraten im HKM weiter verbessert wurden. Solche Ansätze können auch für reale Gase nützlich sein, wenn diese durch harte Kugeln idealisiert werden können. Teilchenmassen werden dabei vernachlässigt bzw. als gleich groß angenommen (= 1).
Es wird anfangs ein festes
Koordinatensystem (Laborsystem) mit kartesischen Koordinaten
betrachtet. Ein Probeteilchen bewegt sich mit der Geschwindigkeit 
vom
Ursprung aus. Die
Geschwindigkeit eines Stoßpartners wird mit 
bezeichnet.
Deren
Relativgeschwindigkeit ist dann 
. Bei Berechnungen werden wegen
der zu
betrachtenden Winkel teilweise Kugelkoordinaten (vgl. z.B. in
Wikipedia) verwendet. Zur Vereinfachung wird außerdem meist ein
Stoßbereich mit doppeltem Durchmesser definiert, so dass alle anderen
Teilchen als punktförmig angenommen werden können. Die hier noch nicht
verwendeten Begriffe sollen für weiterführende Betrachtungen zur
Verfügung stehen:
d Durchmesser der stoßenden Kugeln
L (durchschnittliche) freie Weglänge bis zum nächsten Stoß
n Anzahldichte = Teilchenzahldichte (Teilchenzahl N / Volumen V) mit 0 < n < 1
wegen d > 0
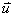Geschwindigkeit
des im
Ursprung startenden Teilchens
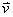Geschwindigkeit
des
Stoßpartners
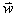Relativgeschwindigkeit
-
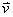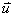
β
Winkel zwischen
-
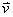und
,
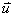also Flugwinkel bzw. Bahnenwinkel
ф Herkunftswinkel der Relativgeschwindigkeit = Kollisionswinkel
Θ
Drehwinkel der Relativgeschwindigkeit bzw. des Flugwinkels um ,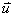
verschwindet
bei sinnvoller Drehung der z-Achse in Ebene mit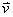
φ Stoßachsenwinkel (Winkel der Berührpunktnormale) erzeugt bzgl. der
Relativgeschwindigkeit, auch Streifwinkel genannt, mit -∏/2<φ<∏/2
θ Drehwinkel der Stoßachse orthogonal um Relativgeschwindigkeit
t Parameter der kontinuierlichen Zeit.
Im betrachteten harte Kugeln Gas (HKG) soll zumindest anfangs davon
ausgegangen werden, dass alle n Ausgangsorte homogen im
dreidimensionalen Raum, also gleichverteilt, vorkommen. Alle
Flugrichtungen seien wegen der Isotropie ebenfalls
gleichwahrscheinlich. Parallele Flugbahnen mit durchschnittlich
gleichen Abständen voneinander sind ebenfalls zulässig (blau). Bewegte
Kugeln mit festem Durchmesser d müssen zwangsweise irgendwann zu Stößen
führen. Zum Zeitpunkt des gegenseitigen Berührens liegt die
Geschwindigkeit 
(Bild
: dick
rot) in beliebiger Richtung vom Ursprung aus. Die Geschwindigkeit 
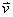eines
betrachteten
Stoßpartners liegt beliebig. Die gebildete Relativgeschwindigkeit wird
durch ihren Betrag w sowie den Winkel 0<θ<∏
von der z-Achse aus und durch den
Drehwinkel 0<Θ<2 ∏
in Kugelkoordinaten beschrieben. Relativ zu dieser ist die Stoßachse
(Berührpunktnormale) auf der Kugel mit dem Durchmesser 2 d durch den
Stoßachsenwinkel φ und den frei wählbaren Winkel θ
definiert.
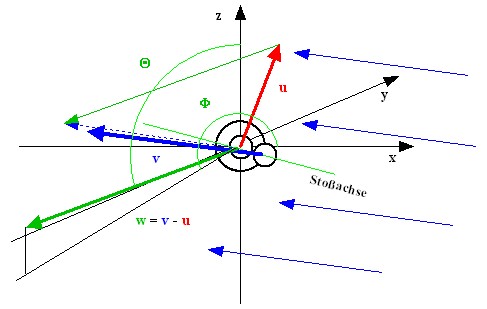
Bild
Im harte Kugeln
Modell
(aktuellere ausführlichere
Definitionen und auch Stoßtransformationen) wird genauer
untersucht, welchen Einfluss die Veränderungen der
Eigenschaften des
betrachteten HKG durch Stöße auf die Häufigkeiten der vorkommenden
Winkel und sonstige Eigenschaften des HKGs haben. Es
wird demnach die richtungsabhängige Stoßhäufigkeit bzw. Stoßfrequenz
untersucht (vgl. auch L. Brendel: B-stoss.pdf).
Das beeinflusst dann weitere Veränderungen bei den Stößen selbst.
Erstes Ergebnis einer Simulation mit Zufallsgeneratoren ist die
Erzeugung der Maxwell-Boltzmannschen (Geschwindigkeits-) Verteilung bei
der Thermalisierung.
Stichworte
(Ende)
Wiese, Lothar: Struktur und
Dynamik der
Materie im Uratom-Modell, http://www.localisator.de/atom, Porec und
Sarajevo 2000-2008
Uratom (Anfang)