FRONTALSTOSSBEWEISIDEE

in dünnem Medium, d.h. bei großer freier Weglänge durch Streuungsbilder der Stoßwahrscheinlichkeit bei variablem b unter gleichzeitiger Variation von f

Die folgende Idee, welche auf dem Vektorwinkel ß aufbaut, erwies sich mittlerweile durch die freundliche Unterstützung von Lothar Brendel (Uni´s Duisburg und Montpellier, Stand Mitte 2001) als möglicherweise falsch, weil die Asymmetrie nur scheinbar erzeugt wird (vgl. betavert.htm). Deshalb ist ein neuer Ansatz mit der Relativgeschwindigkeit in Arbeit, bei dem bisher keine dichteabhängige, aber eine generelle Asymmetrie erkennbar ist. Interessenten koennen per E-Mail die derzeitigen Entwürfe als .pdf Dateien anfordern.

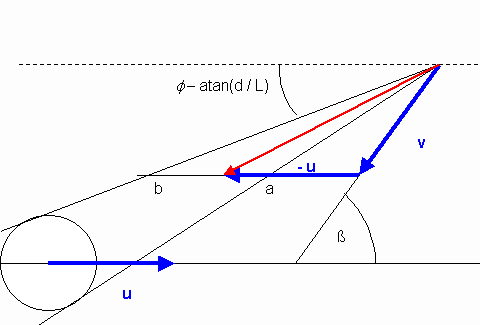
Aus dem Kegelabschnitt der für einen möglichen Stoß zulässigen Relativgeschwindigkeiten der Geschwindigkeitsvektoren v und u ergeben sich die Geschwindigkeitswerte a und b als Funktionswerte für die Integrationsgrenzen von u. Dabei ist die Richtung von u fest in x-Richtung, wobei der Startpunkt im Ursprung liege. Der Startpunkt von v sei (r,f) und b sei der Winkel, mit dem das Uratom im fest gewählten Koordinatensystem auf das mit der Geschwindigkeit u auftrifft.

sind zur Veranschaulichung willkürlich gewählte Werte, welche bei der weiter unten beschriebenen Simulation bei jedem Durchlauf neu angepaßt werden. Die hier willkürlichen Zahlen im Verhältnis zum Uratomdurchmesser 1 sind wegen der anfänglichen Graphiken erforderlich.

Zu jedem Radius r werden nun in der Funktion fu winkelabhängige Häufigkeiten von möglichen Stößen ermittelt. Diese sollen gespeichert werden, um in einer folgenden Analyse eine Häufigkeitsverteilung des Stoßvektorwinkels b in Abhängigkeit von der mit r zusammenhängenden freien Weglänge bzw. Anzahldichte angeben zu können.

In einem weiteren Schritt soll dann durch simulierte zufällige Stöße auch die Geschwindigkeitsverteilung und deren Parameter s angepaßt werden, was hier aber noch nicht dargestellt wird, weil es für den eigentlichen Beweis nicht erforderlich ist.

Die meiste Wahrscheinlichkeitsmasse der untersuchten Normalverteilungen muß in einem Bereich innerhalb des Hauptanteils der Glockenkurve liegen, was natürlich vom Erwartungswert a und der Streuung s (zur Sicherheit hier 3 s) der Geschwindigkeitsverteilung abhängt. Die in der Skizze gezeigten Integrationsgrenzen sind natürlich außer davon hauptsächlich von den beiden Winkeln abhängig, weshalb die Ermittlung einfach nach dem Satz von Pythagoras erfolgt.

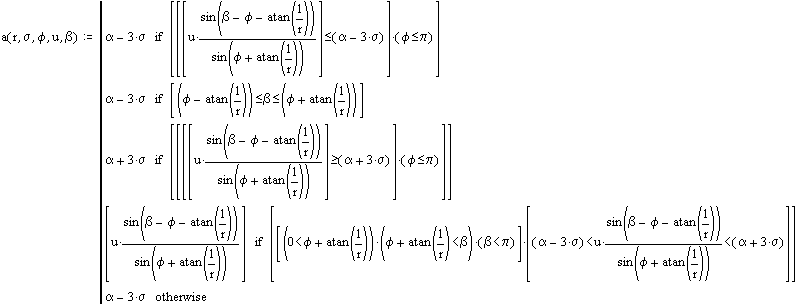
und

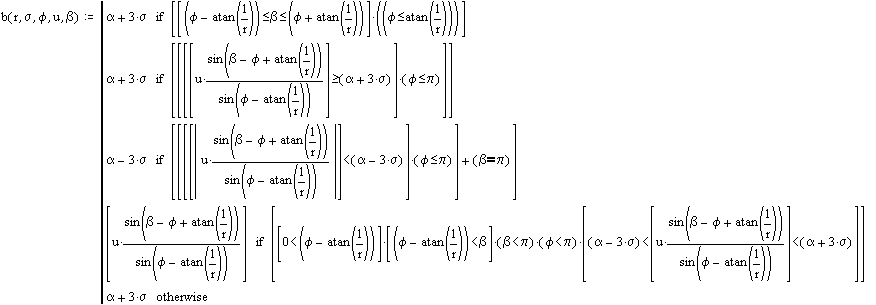
Mit diesen Werten werden aus der bedingten Normal-Verteilungsdichte durch Integration über alle zulässigen Geschwindigkeits-Kombinationen die Wahrscheinlichkeiten für alle möglichen, d.h. zu einem Stoß von einem beliebigen Raumpunkt aus führenden, Geschwindigkeitsvektoren ermittelt, wobei die heuristische Erfahrung aus vielen Vorabsimulationen verwendet wird, daß nur Geschwindigkeiten nahe 1 zu einem Stoß führen können, falls die Herkunft genügend groß angenommen wird. Zur Vereinfachung wird der Öffnungswinkel b verwendet, welcher den absoluten Auftreffwinkel bei dem Stoß darstellt. Der Uratomdurchmesser beträgt d = 1 unter der gleichzeitigen Annahme, daß die Betrachtung einer durchschnittlichen Entfernung von r = l, d.h. der durchschnittlichen freien Weglänge l, ausreicht. Der zulässige Raumwinkel f < b liegt somit auf einem Kreis mit dem Radius r.

Vorerst wird der Parameter als fest angenommen (Vakuumserwartungswert).

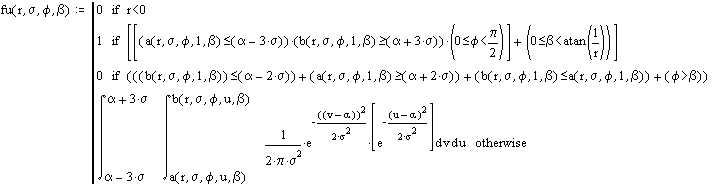
Eine feste Durchschnittsgeschwindigkeit von 1 wird bei der Bestimmung der außerhalb der Glockenkurve liegenden Wahrscheinlichkeiten angenommen, weil Mathcad die numerische Integration nicht von Null bis Unendlich löst.

Anstelle Null und unendlich müssen leider numerisch beherrschbare kleine und große Werte in Abhängigkeit von a und s verwendet werden, was schon bei der Definition von a und b erwähnt wurde.

Für alle r,f und b muß dies eine WV-Dichte sein, d.h. das Integral muß den Wert 1 haben.

Zur Simulation mit vielen verschiedenen Größenordnungen wird nach jedem Rechendurchlauf die um 1 veränderte Durchlaufzahl k gespeichert.

Wegen der ebenfalls heuristisch festgestellten Häufung um kleine b werden zur graphischen Darstellung und wegen der Rechenzeitbegrenzung nur m Werte b nahe den zu erwartenden Frontalstoßwinkeln betrachtet.

Anstelle der freien Weglängen werden viele verschiedene Anfangsorte (r,f), mit bei jedem Programmdurchlauf größer werdendem r, untersucht.

sind der Herkunftsabstand und die anfängliche Streuung der Geschwindigkeiten und der Beweis muß für viele sich durch Stöße an mögliche Grenzwerte anpassende Werte geführt werden.

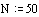
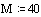
  b-Werte und f-Werte

Eine Häufung möglicher Raumwinkel f ergibt sich um b/2, weil durchschnittlich gleich lange Geschwindigkeitsvektoren betrachtet werden.

Vorerst können aber nur m einzelne Werte f in die Funktion fu(r,s,f,b) eingesetzt werden, benötigt wird jedoch eine Wahrscheinlichkeitsdichte, über deren Integration die einem Stoßwinkel b zugeordnete relative Häufigkeit solcher Stöße ermittelt werden soll.

Bei dieser Betrachtung kommen die Herkunftswinkel f, wegen f < b, bei größer werdendem b immer wieder vor und deren Wahrscheinlichkeitsmassen werden mehrmals summiert bzw. integriert. Deshalb ist es gut, daß die häufigsten Wahrscheinlichkeiten um b/2 konzentriert sind. Mit geeigneten Schrittweiten, also n und m, ergibt sich ein Gitter, bei dem fast alle Wahrscheinlichkeitsmasse in beinahe unabhängigen Maschen konzentriert ist (ähnlich Gitter-Eichtheorie). Für die hier vorerst zu ermittelnde graphische Darstellung hat das keine Bedeutung. Die auftretende Häufung bei kleinen b würde sogar noch verstärkt, wenn die bereits einmal berücksichtigten Herkunftswinkel f abgezogen würden.

Es werden demnach m mal n Werte in der Matrix F gespeichert.

Mit den so für viele Geschwindigkeitsstreuungen s und Herkunftsorte r erzeugbaren hier graphisch dargestellten fu-Werten sollen nur die wesentlichen Eigenschaften für die Vektorwinkelwahrscheinlichkeiten b weiter verwendet werden.

Winkelwahrscheinlichkeiten und deren mögliche Funktionen:

Aus den Funktionswerten (Wahrscheinlichkeitsprodukt der möglichen Geschwindigkeitsbeträge) der zu Stößen führenden Herkunftsorte und möglichen Auftreffwinkel werden nun Durchschnittswerte als Parameter möglicher Wahrscheinlichkeitsverteilungen der Auftreffwinkel in Abhängigkeit von der freien Weglänge ermittelt.

Die in fu auftretenden Nullen stellen zwar eigentlich sehr kleine Wahrscheinlichkeiten für das Auftreten eines Stoßes mit den zugeordneten Winkeln und Geschwindigkeitsintervallen dar, diese sind aber so klein im Verhältnis zu den noch durch Mathcad berechneten, daß sie vernachlässigt werden können. Der Mittelwert der auftretenden Winkel liegt wegen der Auszeichnung der einen Bewegung in x-Richtung für Herkunfts- und Auftreffwinkel bei Null. Aufgrund des Augenscheines, daß bei großen Winkeln gegen p die fu-Werte verschwinden für alle großen freien Weglängen (der Bereich von p bis 2 p wird wegen seiner Symmetrie durch einen Faktor berücksichtigt), wird eine Verwendbarkeit der Gausschen Normalverteilung als zulässiger Verteilung bei einer freien Weglänge als möglich angenommen. Der Erwartungswert von b ist demnach Null und die Streuung ermittelt sich aus den zuerst zu Normalverteilungen gemachten, also normierten fu-Werten:

 sind die Summen der fu´s, welche stellvertretend als Gewichte der auftretenden Wahrscheinlichkeiten pro Winkel (b Index n, f Index m) genommen werden.

ist der notwendige Normierungsfaktor zur Bestimmung von

Mit diesen Streuungen ergeben sich demnach n Wahrscheinlichkeitswerte für die zugeordneten n Auftreffwinkel b .

zeigt, daß es sich tatsächlich um Wahrscheinlichkeiten handelt.

Die Funktion p läßt sich bisher nicht einfach durch eine bekannte Wahrscheinlichkeits-Funktion, wie die Exponentialverteilung beschreiben, obwohl ihr bei großen r die Hyperbel 1/ (4 n +1) nahe kommt. Deshalb sollen die tatsächlichen p-Werte in einer Datei für verschiedene r gespeichert werden. Für jede untersuchte Geschwindigkeitsstreuung s wird eine eigene Datei erzeugt, an welche nach einer Hilfsspeicherung Werte angehängt werden können.

Für steigende Werte von r (wächst mit der Zahl k der gespeicherten Werte) kann nun hier auch eine dreidimensionale grafische Darstellung angegeben werden:

Die Streuungen sbeta nehmen offensichtlich mit wachsendem i (natürlich wieder zusammenhängend mit r) ab:

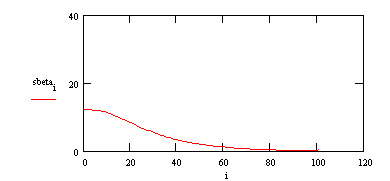
Wichtig wäre nun, eine Funktion zu finden, die für beliebige Geschwindigkeitstreuungen s und Anzahldichten gilt, welche durch Herkunftsentfernungen r beschrieben werden sollen.

Zum Vergleich wird eine Hyperbel verwendet, weil weder die konstruierbare Normal- noch die Lognormalverteilung oder Exponentialverteilung dem tatsächlichen Verlauf der ermittelten Häufungen nahe kommen.

Versuchsweise können Graphen verschiedener Funktionen betrachtet werden, z.B.:

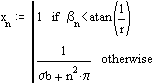
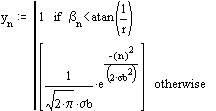
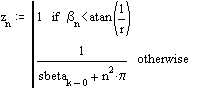
Für die Untersuchung einer etwas größeren Datenmenge mit MathConnex wurden viele fu-Werte, welche ja stellvertretend für Häufigkeiten von auftretenden Vektorwinkeln genommen werden, nach folgenden willkürlichen Formeln zur Ermittlung der r und s zugeordneten Tabellenplätze, verwendet:

i:=0..300, hier im Beispiel j:=0..60, hier

für i Zeilen und j Spalten d.h.

.

Auch die Wahrscheinlichkeiten und Streuungen müssen für den kleinen Abstand neu ermittelt werden:

In vielen heuristischen Versuchen wurde nun eine Funktion w ermittelt, welche annähernd die Häufigkeiten der Vektorwinkel b für verschiedene r und s beschreibt. Nur zur vereinfachten Schreibweise wurde die Parameterfunktion fk(r,sb) herausgezogen.

Bei diesem kleinen Abstand r ist die neu definierte Funktion graphisch dargestellt, welche sich für größere Werte r (>100) immer besser dem Graphen wie im obigen Beispiel annähert.

Hier sollen nun zum Abschluß des Beweises die gesammelten Daten, also gespeicherten Vektorwinkelstreuungen analysiert werden.

Die Streuungen von auftretenden Vektorwinkeln der möglichen Stöße nehmen mit zunehmender Herkunftsentfernung r bei allen (hier untersuchten) Geschwindigkeitsstreuungen s ab, was auch schon erwartet war. Die graphische Darstellung verdeutlicht das noch besser, weil auch die in der Tabelle nicht gezeigten Werte dargestellt werden. Lücken ergeben sich nur weil bisher nicht alle Werte ermittelt wurden.

Dieser Zusammenhang kann als Beweis für in dünnem Medium häufiger auftretende Frontalstöße angesehen werden.

Der Bereich starker Abnahme von Streuungen dürfte im dichten Medium für die starke Wechselwirkung von besonderer Bedeutung sein, weil von solchen Vektorwinkelverteilungen mit häufigem Vorkommen aller möglichen Winkel oft neue große Geschwindigkeitsunterschiede erzeugt werden. Sehr kleine Streuungen müssen für das Vakuum besonders im Hinblick auf eine Rückkopplung im Sinne der gegenseitigen Beeinflussung zur Erzeugung der elektromagnetischen Erscheinungen untersucht werden. Dabei kommt es auch schnell zu einem Ausgleich der Geschwindigkeitsvektorlängen, für welche sich in Abhängigkeit der Anzahldichte ein konstantes s einpendeln sollte.

Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)