Zufällige Stöße
Das Folgende basiert
auf dem Wunsch, einmal etwas genauer zu untersuchen, was in einem wirklich
einfachen Gas harter Kugeln geschieht. Dieser Wunsch entspringt der Idee aus http://uratom.de . Die
Definitionen und einige weitergehende Überlegungen sind in Bearbeitung, aber
als Entwurf unter http://uratom.de/Beweise/Definitionen.htm
zu finden. Im betrachteten Raum ist keine Richtung vor der anderen
ausgezeichnet. Beim Zusammenstoß wird nur die zur Stoßachse parallele
Geschwindigkeit ausgetauscht. Stoßachsen können zufällig relativ zu den
vorkommenden Vektorwinkeln erzeugt werden, wobei vorläufig davon ausgegangen
wird, dass parallele Flugbahnen gleichwahrscheinlich sind. Trotzdem handelt es
sich noch um ein orts- und zeitloses Gas, weil Orte vorerst nicht betrachtet
werden. Einige Eigenschaften der Geschwindigkeitsänderungen bei vielen
Zusammenstößen einfacher Kugeln sollen untersucht werden. Die stoßenden
Vektoren u und v haben jeweils 3 Komponenten. Für die Stoßachsenermittlung
ist zuerst die Relativgeschwindigkeit erforderlich.
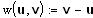
(1)
Die Richtung der Relativgeschwindigkeit wird
mit der Kugelkoordinaten-Transformation ermittelt, für die hier die in
Mathcad eingebaute Funktion verwendet wird:
(2)
(3)
Bei den Ergebnissen mit der ausführlichen
Transformation gemäß dem Artikel über Kugelkoordinaten in Wikipedia, nimmt F Werte von 0 bis 2 p an.
Die Stoßachsenwinkel ergeben sich i.A. zufallsabhängig,
wobei gleichwahrscheinliche parallele Bahnen zur Richtung der
Relativgeschwindigkeit angenommen werden. Das ist auf gleichwahrscheinliche
parallele Bahnen bei den Stoßpartnern zurückzuführen. Damit ergibt sich in
kartesischen Koordinaten der Stoßachsenvektor:
(4)
Dieser wurde relativ zur Richtung der
Relativgeschwindigkeit w(u,v) erzeugt und muss nun im ursprünglichen
Koordinatensystem (dem Laborsystem von u und v) ausgedrückt
werden, was durch zwei hintereinander ausgeführte Drehungen erreicht wird:
(5)
(6)
Damit ergibt sich die Stoßachse im ursprünglichen
Koordinatensystem durch das zweifache Zurückdrehen zu:
(7)
Dieses S entspricht beim Zentralstoß auf
eine ruhende Kugel dem ursprünglichen u bzw. beim Zentralstoß auf ein
beliebiges v allgemeiner dem Relativgeschwindigkeitsvektor w normiert
auf 1.
Beim Stoß werden nun die zur Stoßachse
parallelen Geschwindigkeiten der beiden beteiligten Kugeln ausgetauscht. Alle
Vektoren sollen jedoch weiterhin im ursprünglichen Koordinatensystem
betrachtet werden.
(8)
parallele Geschwindigkeiten
(9)
(10)
orthogonale Geschwindigkeiten
(11)
(12)
Geschwindigkeiten nach Stoß
(13)
Für die Simulation von Stößen
(ortsloses Gas) werden die eingehenden Parameter zufällig erzeugt. Zuerst die
Stoßachsenwinkel, die auf der Annahme gleichwahrscheinlicher paralleler
Bahnen beruhen:
(14)
(15)
Dann werden die
Geschwindigkeitsvektoren so konstruiert, dass u in z-Richtung liegt:
Für die Geschwindigkeitsbeträge u
und v wird ebenfalls ein Zufallsgenerator benötigt. Anfänglich wird davon
ausgegangen, dass es sich um ein genügend großes dünnes Medium handelt, so
dass die Geschwindigkeitsbeträge unabhängig von vorherigen Stößen sind.
Als Geschwindigkeitsverteilung wird deshalb eine so verschobene
Maxwellverteilung verwendet, dass die Durchschnittsgeschwindigkeit 1 wird und s dem entsprechend
(= 0.62665706868 ). Als
Wahrscheinlichkeitsdichte verwende ich deshalb:
(16)
Damit ergibt sich die für den
Zufallsgenerator verwendbare Wahrscheinlichkeitsverteilung:
mit
(17)
Demnach erhalten wir für die zufälligen
Geschwindigkeitsbeträge der beiden Stoßpartner:
(18)
bzw.
(19)
was wir mit der root Funktion lösen,
die nur vorher mit einer Zahl aus dem Lösungsintervall initiiert wird.
0<U<1 bzw. 0<V<1 sind die zufälligen Funktionswerte des
Zufallsgenerators.
(20)
(21)
(22)
(23)
Darüber hinaus wird nun ein zufälliger
Winkel für den Stoßpartner (Flugwinkel = Bahnenwinkel) ermittelt. Dafür
wird eine zufällige Verteilung wie z.B. die aus der von L. Brendel in "B-stoss.pdf" ermittelten Wahrscheinlichkeitsdichte
w(u,b) (69) verwendet. Das entspricht
einem zufälligen Q = p - b in
Kugelkoordinaten. Hier wird vorerst folgende einfachere Verteilung verwendet,
die einen ähnlichen Verlauf zeigt:
(24)
(25)
Zur Nullstellenbestimmung wird die Lösungsmenge
mit einer Näherungslösung aus dem zulässigen Intervall initiiert.
0<y<1 ist der zufällige Funktionswert des Zufallsgenerators.
(26)
(27)
sowie dann die root-Funktion
verwendet:
(28)
Außerdem muss noch F der Drehwinkel des Vektors v um die
Richtung von u zufällig bestimmt werden. Das geht wie für den Winkel f:
mit z.B.
(29)
Die so ermittelten sechs Parameter
definieren demnach ein Stoßgebilde, das mit den Stoßtransformationen sechs
neue Parameter für die Bewegung der zwei Teilchen nach dem Stoß ergibt. Um
die obigen Stoßtransformationen (12) und (13) verwenden zu können, müssen
die Geschwindigkeitsvektoren noch in kartesische Koordinaten umgerechnet
werden. Sinnvollerweise wird u in z-Richtung gelegt:
(30)
(31)
Damit ergeben sich nach dem Stoß die
beiden Geschwindigkeitsvektoren:
(32)
(33)
Damit kann beispielsweise ermittelt
werden, wie sich die Geschwindigkeitsbetragssummen vor und nach dem Stoß
zueinander verhalten:
oder
Interessant wird es nun bei vielen Stößen.
Was passiert dann?
Zur bequemeren Speicherung für eine
spätere Auswertung nach vielen Stößen werden die Parameter vor dem Stoß
und nach dem Stoß zuerst noch zu einem Gebilde zusammengefasst.
also
(34)
Bei jeder Neuberechnung des gesamten
Dokuments werden neue zufällige Werte ermittelt. Diese werden einfach zur späteren
Auswertung an eine Datei PSI angehängt.
(35)
Zur Analyse der Daten werden diese
eingelesen und aus ihnen die interessierenden Elemente ermittelt, indem die
Gesamtzahl durch 12 geteilt wird.
(36)
(37)
Die Zahl der Durchläufe und damit Stöße
ist demnach hier
also
.
(38)
Für
(39)
ergeben sich die Geschwindigkeitsbeträge
vor und nach dem Stoß:
(40)
(41)
(42)
(43)
Damit können nun die Veränderungen
bei den Geschwindigkeitsbeträgen verfolgt werden. Zuerst interessiert
beispielsweise die Gesamtveränderung:
(44)
Nach den Stößen sind die Summen der
Geschwindigkeitsbeträge interessanterweise stets kleiner als 2, demnach
kleiner als vor den Stößen.
Als Durchschnittswert ergibt sich
nach den betrachteten z Stößen:
hier demnach
(45)
Bei sehr großen Stoßzahlen strebt
diese Zahl sicher gegen einen Grenzwert, der in einer Uratomtheorie eine
wichtige physikalische Bedeutung haben sollte.
Die einzelnen Geschwindigkeitsbeträge
sind auf den ersten Blick nicht nach der Maxwell-Verteilung verteilt. Bei
vielen Stößen harter Kugeln, die bereits einer Maxwell´schen
Geschwindigkeitsverteilung unterliegen, bleibt diese aber erhalten, was auch
schon bekannt ist (vgl. z.B. L. Brendel: B-stoss.pdf,
Abbildung 10). Hier kann der sich ergebende Geschwindigkeitsmittelwert zur
Normierung aller Teilchengeschwindigkeiten verwendet werden. Es gilt:
(46)
(47)
Der Geschwindigkeitsmittelwert aller
Kugeln nach den Stößen ist demnach
(48)
Durch diesen werden alle ermittelten
Geschwindigkeitsbeträge geteilt. Die alternative Normierung mit (36) bzw.
(37) ergibt numerisch hier in Mathcad unten (38) eine geringfügig abweichende
durchschnittliche Varianz:
(49)
(50)
Mit diesen neuen Geschwindigkeiten
wird nun deren Verteilung überprüft:
(51)
(52)
Dabei gilt natürlich:
Die Varianzen werden damit
(53)
(54)
Damit wird
(55)
die durchschnittliche Varianz aller
Teilchen nach den Stößen. Eine physikalische Interpretation wäre wohl hier
noch verfrüht.
Andererseits kann leicht gezeigt werden, dass in
einem HKG aus lauter Teilchen mit dem Geschwindigkeitsbetrag 1 bei vielen Stößen
eine neue niedrigere Durchschnittsgeschwindigkeit entsteht. Assoziieren wir
dieses HKG mit einem Uratomäther oder dem Feld der verborgenen Parameter
(oder versteckten Variablen bzw. Führungsfeld) der Bohmschen Mechanik,
ergibt sich eine gewisse Berechtigung zu weiteren Spekulationen.
Für die Geschwindigkeitsbeträge u
und v wird, wie oben erwähnt, eigentlich ebenfalls ein Zufallsgenerator benötigt.
Anfänglich sind wir davon ausgegangen, dass es sich um ein genügend großes
dünnes Medium handelt, so dass die Geschwindigkeitsbeträge unabhängig von
vorherigen Stößen sind. Als Geschwindigkeitsverteilung wird deshalb eine so
reskalierte Maxwellverteilung verwendet, dass die Durchschnittsgeschwindigkeit
1 wird und s dem entsprechend
.
(56)
Als Wahrscheinlichkeitsdichte für
eine Erwürfelung zufälliger Maxwell- verteilter Geschwindigkeiten ergibt
sich deshalb:
(57)
Damit ergibt sich deren Streuung zu:
(58)
entsprechend
.
Eine solche
Geschwindigkeitsverteilung ist in sehr vielen Versuchen bestätigt und somit
der Standardfall unserer natürlichen Umgebung. Deshalb liegt es nahe,
einfach zu versuchen, was für einen Mittelwert beispielsweise das Produkt der
Varianz aus (58) und der mittleren Geschwindigkeitsveränderung (45) bzw.
besser (62) ergibt.
Um die Entwicklung für alle Einzelstöße
nachvollziehen zu können, wird auf die gespeicherten Resultate folgendes
Verfahren angewandt:
Also
(59)
(60)
Dies sind die
Geschwindigkeitsabnahmen-Durchschnitte bis zum entsprechenden Stoß und
(61)
die entsprechenden
Geschwindigkeitszunahmen-Durchschnitte.
Für alle betrachteten Stöße wird
demnach der Mittelwert der Geschwindigkeitsveränderung ermittelt und für die
graphische Darstellung zwischengespeichert:
(62)
Noch einfacher ist die direkte
Betrachtung der Entwicklung der Geschwindigkeitsänderungen aus (44) bei
vielen Stößen:
(63)
Mit dem Vergleichswert:
(Feinstrukturkonstante), ergibt sich
damit beispielsweise folgende Entwicklung dieser Werte für
Stöße:
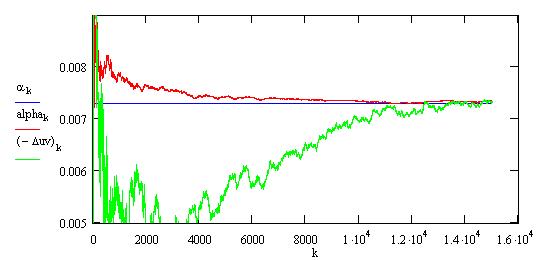
Verschiedene in der gleichen Größenordnung
liegende Kennzahlen ergeben sich auf ähnliche Art, wenn anstelle (16), (17)
oder (28) zufällige Geschwindigkeiten bzw. Winkel mit anderen
Wahrscheinlichkeitsverteilungen erwürfelt werden. Die gesamten Ergebnisse
sind ein starkes Indiz für die Berechtigung des Harte Kugeln Modells
als Konkurrenz für (Super-)
Stringmodelle , Loop-Quantengravitation
oder Äthertheorien, welche derzeit zur Lösung der Frage, was die Welt im
Innersten zusammenhält, favorisiert werden.
Es scheint ein physikalisches Modell für die
Erzeugung und damit der erstmaligen Erklärung der Feinstrukturkonstante
in Aussicht zu stehen. Die hier noch spekulative physikalische Deutung ist die
Interpretation als Konstante des Mittelwertes aus der durchschnittlichen
Wechselwirkung zwischen Vakuum-Atomen und wie auch immer erzeugten Systemen
aus diesen "Uratomen".
Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im
Uratom-Modell, http://www.localisator.de/atom, Porec und Sarajevo 2000-2005
Uratom (Anfang)
![]()