Vereinheitlichung der Wechselwirkungen

Die theoretische Physik beschreibt die Bausteine der Materie und die Kräfte, die zwischen ihnen wirken. Diese Kräfte bezeichnet man auch als Wechselwirkungen. Sie sorgen dafür, dass die Bausteine oder Teilchen sich anziehen oder abstoßen. Ein Beispiel für eine solche Wechselwirkung ist die elektromagnetische Kraft, die auf elektrisch geladene Teilchen wirkt. Weitere Kräfte sind die so genannte schwache und die starke Kernkraft, die für die Bindung der Atomkerne und für weitere subatomare Strukturen, wie z.B. die Quarks, eine wichtige Rolle spielen. Alle drei genannten Kräfte spielen in der Elementarteilchenphysik eine wichtige Rolle und lassen sich mit einer einheitlichen physikalischen Theorie beschreiben, dem so genannten Standardmodell der Elementarteilchen. Diese Theorie ist eine Quantentheorie, d.h. für die so beschriebenen Teilchen gibt es eine Wahrscheinlichkeitsinterpretation, die zu dem bekannten Welle-Teilchen-Dualismus führt.

Die vierte und letzte der bekannten Wechselwirkungen ist die Schwerkraft oder Gravitation. Sie bewirkt die Anziehung zwischen Massen und wird mit der Einsteinschen Allgemeinen Relativitätstheorie beschrieben, nach der die Anziehung von Massen durch die Krümmung des Raums bewirkt wird. Die Relativitätstheorie ist keine Quantentheorie, sondern eine klassische Theorie, in der Ort und Geschwindigkeit der Teilchen für alle Zeiten gleichzeitig angegeben werden können.

Schon Einstein selbst benannte vor siebzig Jahren als fundamentale Aufgabe der Physik die Beschreibung aller vier fundamentalen Wechselwirkungen in einer einzigen vereinheitlichten Theorie. Diese Aufgabe ist bis heute nicht vollständig gelöst. Ein wesentliches Problem ist, dass sich die Relativitätstheorie - im Unterschied zur Theorie der drei übrigen Wechselwirkungen - nicht auf herkömmliche Weise als Quantentheorie schreiben lässt. Daher ist es schwierig, die Gravitation in die Theorie der drei übrigen Wechselwirkungen zu integrieren. Es hat in dieser Richtung jedoch schon wesentliche Fortschritte gegeben: Insbesondere ist die Stringtheorie ein möglicher Kandidat für eine vereinheitlichte Theorie.

Stringtheorie und Membranen

In der Stringtheorie wird das Problem der Quantisierung der Gravitation dadurch gelöst, dass die fundamentalen Teilchen nicht mehr wie in Quanten- und Relativitätstheorie als punktförmig angesehen werden, sondern eine Ausdehnung haben. Durch die endliche Ausdehnung der Strings wird nämlich das Verhalten von quantenmechanischen Streuprossen mit Spin 2-Gravitonen, die als Kraftteilchen in der Quantengravitation auftreten, dahingehend beieinflusst, dass alle Unendlichkeiten abwesend sind, die die Quantisierbarkeit der Gravitationskraft mit Punktteilchen im Rahmen der
Störungstheorie bislang unmöglich gemacht hat.
Dies ist ein wichtiger Fortschritt im Hinblick auf die Vereinheitlichung der Wechselwirkungen. Zunächst wurden im Rahmen der Stringtheorie die Teilchen durch Anregungsmoden eindimensionaler ausgedehnter Objekte beschrieben, also durch Fäden oder Saiten („strings“), die in einer Raumrichtung ausgedehnt sind. Seit 1995 hat sich die Stringtheorie dahingehend weiterentwickelt, dass auch mehrdimensionale ausgedehnte Objekte, Membranen oder auch genannt p-Branen, betrachtet werden. 0-Branen sind gewönliche Teilchen, 1-Branen sind eindimensionale Fäden, 2-Branen zweidimensionale Flächchen, die auch Membranen genannt werden. Ebenso gibt es auch 3-Branen, 4-Branen, usw. Die theoretischen Entwicklungen der letzen zehn Jahre deuten stark darauf hin, dass es eine bislang nicht bekannte vereinheitlichte Theorie in elf Raum-Zeit Dimensionen gibt, die alle diese Objekte in mathematisch konsistenter Weise beschreibt.

In der Stringtheorie entsprechen die herkömmlichen Punkteilchen den niedrigsten harmonischen Schwingungsmoden des Strings, wobei man im wesentlichen zwei verschiedene Typen von Strings betrachtet, nämlich den geschlossenen String und den offenen String, der einen Anfangspunkt und auch einen Endpunkt besitzt. Auf diese Art und Weise wird die Vielfalt der Elementarteilchen auf zwei fundamentale Freiheitsgrade reduziert, also erstmal eine enorme Vereinfachung im Vergleich zum Standardmodell der Elementarteilchenphysik. Bei hohen Energien können natürlich immer mehr und mehr Schwingungsmoden eines Strings angeregt werden, die sehr schweren, d.h. massereichen Teilchen entsprechen. Der experimentelle Nachweis dieser schweren Stringteilchen würde gewissermassen den „Beweis“ der Stringtheorie darstellen, ist aber experimentell sehr schwierig oder gar praktisch unmöglich, da sich die so genannte Stringmassenskala jenseits der Energieskala des Standardmodells (einige 100 GeV) befinden muss, und u.U. mit der Planck-Skala von 10¹⁹ GeV zu identifizieren ist. Diese gigantischen Energien sind weit jeinseits der Möglichkeiten derzeitiger (und wohl auch zukünftiger) Teilchenbeschleuniger. Deswegen sucht man auch nach indirekten Spuren von Strings, insbesondere nach der so genannten Supersymmetrie, die zu jedem bekannten Elementarteilchen ein supersymmetrisches Partnerteilchen mit gleichen Quantenzahlen aber unterschiedlichem Spin postuliert. Die Suche nach der Supersymmetrie wird einen Hauptschwerpunkt der Forschung des LHC´s (Large Hadron Collider) am CERN darstellen, der seine Arbeit im Jahre 2008 aufnehmen wird, und an dem das Max-Planck-Institut für Physik im Rahmen des ATLAS-Experimentes (A Toroidal LHC Apparatus) maßgeblich beteiligt ist.

Auch wenn die Stringtheorie das Problem der Quantisierung der Gravitation prinzipiell löst, so bleiben noch viele Fragen zu erforschen. Einerseits lässt sich die Stringtheorie bisher nur unter Verwendung bestimmter Näherungsverfahren formulieren, andererseits muss noch geklärt werden, wie die Stringtheorie sowohl mit den eingangs erwähnten Quantentheorien der Elementarteilchenphysik als auch mit der Relativitätstheorie zusammenhängt. Die Stringtheorie beschreibt nämlich die Physik bei sehr hohen Energien, so hoch, dass heute kaum denkbar ist, sie jemals im Experiment zu erreichen. Im Grenzfall niedrigerer, im Teilchenbeschleuniger erzeugbarer Energien jedoch, d.h. wenn die Auflösung so grob wird, dass die Fäden nur noch punktförmig erscheinen, muss die Stringtheorie in die heute bekannten Theorien der Quanten- und Relativitätstheorie übergehen. Dabei erwartet man, dass die Stringtheorie auf neue physikalische Phänomene in diesem Energiebereich hinweist und neue Beziehungen zwischen bisher unabhängigen Parametern herstellt. Aufgrund aktueller Forschungsergebnisse zeichnet sich ab, dass sowohl bei der exakten Formulierung der Stringtheorie bei hohen Energien als auch bei der Beantwortung der Frage nach dem niederenergetischen Grenzfall die Membranentheorie eine zentrale Rolle spielen wird.

Mit verschiedenen Aspekten der Stringtheorie beschäftigt sich auch die Abteilung Quantenfeldtheorie und Stringtheorie am Max-Planck-Institut für Physik in München. Insbesondere stehen folgende zwei Themenschwerpunkte im Mittelpunkt des Interesses.

1.) Stringkompaktifizierungen und Membranen-Welten

Eine der wichtigsten Erkenntnisse in der Stringtheorie ist es, dass ein String neun Raumrichtungen benötigt, um seine Schwingungen in mathematisch konsistenter Art und Weise durchzuführen. In der Superstringtheorie ist die Raum-Zeit also nicht vierdimensional, wie in der herkömmlichen Quantenfeldtheorie oder wie auch in der Allgemeinen Relativitätstheorie, sondern die Stringtheorie muss in eine 10-dimensionale Raum-Zeit mit neun räumlichen Richtungen eingebettet werden. Mathematisch gesehen stellt ein höherdimensionaler Raum nichts Außergewöhnliches dar.
Im drei-dimensionalen euklidischen Raum lässt sich jede Bewegung in Nord-Süd, West-Ost und, in der vertikalen Richtung, in Aufwärts und Abwärts zerlegen. Das bedeutet, dass man an jedem Punkt der zwei-dimensionalen Ebene eine dritte, vertikale Raumrichtung aufspannen kann. Genauso verhält es sich z.B. mit einem vier-dimensionalen Raum: Über jedem drei-dimensionalen Raumpunkt gibt es eine vierte Bewegungsrichtung. Um nun in der Stringtheorie zu erklären, warum unser beobachtetes Universum nur drei Raumdimensionen besitzt, bedient man sich einer analogen Beschreibungsweise des neun-dimensionalen Raumes: Man nimmt an, dass es über jedem Punkt im vier-dimensionalen Raum-Zeit-Kontinuum einen sechsdimensionalen Raum gibt, der in sich gesehen eine kompakte Mannigfaltigkeit darstellt (Abb. 1).

Abb. 1: Kompaktifizierung: an jedem Punkt des 3-dimensionalen Raumes, hier als Ebene dargestellt, ist ein kompakter 6-dimensionaler Raum aufgehängt, der hier die Form eines Torus annimmt.

Dieser sechs-dimensionale Raum kann also als ein verallgemeinerter Kreis oder auch als verallgemeinerter Torus angesehen werden, da seine Richtungen periodische Gebilde darstellen. Diesen Vorgang nennt man Kompaktifizierung von sechs Raumrichtungen. Ein Spezialfall von sechs-dimensionalen, kompakten Mannigfaltigkeiten, sind die Calabi-Yau-Räume, die sich in der Stringtheorie als besonders wichtig herausgestellt haben. Nun stellt sich sofort die physikalische Frage, warum die zusätzlichen sechs Dimensionen in der Stringtheorie bislang noch nicht entdeckt wurden. Hierfür gibt es im wesentlichen zwei mögliche Antworten:

Erstens, die extra Dimensionen sind kleiner als ca. 10^{-16}cm. Das bedeutet, dass man gemäß der Heisenbergschen Unschärrferelation Energien benötigt, die höher als ca. 100 GeV sind, um mit Teilchenbeschleunigern die extra Dimensionen aufzulösen, d.h. sichtbar zu machen.
Dieser Umstand kann auch etwas anders beschrieben werden: falls ein Teilchen sich im höherdimensionalen Raum bewegen kann, besitzt seine Wellenfunktion immer einen vier-dimensionalen Anteil, welcher mit einer Wellenfunktion in den extra Raumrichtungen multipliziert wird. Bei periodischen Randbedingungen in den extra Raumrichtungen besitzt der entsprechende Energieoperator ein diskretes Spektrum, eine Tatsache, die impliziert, dass jedes bekannte Elementarteilchen, z.B. ein Quark, ein Elektron oder auch ein Photon, von unendlich vielen, angeregten Teilchen begleitet wird, die sich von den bekannten Teilchen nur durch ihre höhere Massen unterscheiden, ansonsten aber identische Eigenschaften besitzen, z.B. hinsichtlich ihrer elektrischen Ladung. Diese Teilchen nennt man nach Theodor Kaluza und Oskar Klein Kaluza-Klein-Teilchen (KK-Teilchen), wobei die Masse der KK-Teilchen immer durch ein Vielfaches des inversen Radius der extra Dimensionen gegeben ist, also durch ein Vielfaches von mindestens 100 GeV/c². Ein möglicher Nachweis der KK-Teilchen in zukünftigen Beschleunigerexperimenten (LHC in Genf oder Linear Collider) gäbe einen direkten Hinweis auf das Vorhandensein von extra Dimensionen, und somit auch die Existenz vom Strings.

Es gibt aber noch eine zweite logische Möglichkeit, warum sich extra Raumdimensionen uns bislang entzogen haben. Diese hängt mit dem schon erwähnten Vorhandensein von höherdimensionalen Objekten in der Stringtheorie zusammen, nämlich den p-Branen. In Stringmodellen mit offenen Strings und p-Branen können sich die Teilchen des Standardmodells der Elementarteilchenphysik, wie Elektronen, Myonen, Neutrinos, Quarks, Photonen, Gluonen, W- und Z-Bosonen, nur auf einer räumlich gesehen p-dimensionalen, im einfachsten Fall drei-dimensionalen Membrane bewegen, die in den durch die Stringtheorie vorgegeben neun-dimensionalen Raum eingebettet ist. Diese Membrane stellt also gleichermaßen unser beobachtetes Universum dar, in dem sich die Prozesse der Elementarteilchenphysik abspielen.
Als Analogie zu diesem Szenario kann man das Höhlengleichnis von Plato heranziehen. Hier sind einige Gefangene in einer Höhle fest auf eine Steinbank gekettet, sodass sich die Gefangenen nur entlang der Bank (d.h. in x-Richtung) und auch vertikal (also in z-Richtung) bewegen können, aber nicht in transversaler Richtung (y-Richtung) senkrecht zur Bank (Abb. 2).

Abb. 2: Höhlengleichnis von Plato.

Die Höhle wird durch eine Kerze ausgeleuchtet, die die Bewegung der Gefangenen bzw. auch der Gegenstände hinter ihnen auf einen Schirm vor ihnen projeziert. Es ist klar, dass die Gefangenen sich der Illusion hingeben, sie lebten nur in einem zwei-dimensionalen Raum, da ihnen die dritte Raumrichtung verschlossen bleibt. Ganz ähnlich verhält es in der Membranen-Welt der Stringtheorie. Die Teilchen des Standardmodells sind die niedrigsten Anregungsmoden eines offenen Strings, dessen Enden aus Gründen der mathematischen Konsistenz der Theorie im einfachsten Fall auf einem drei-dimensionalen, oder allgemeiner auf einem p-dimensionalen Raum festgeklebt sind (Abb. 3). (In der Stringtheorie bezeichnet man dies auch manchmal alsholographisches Prinzip - siehe auch nächstes Kapitel.)

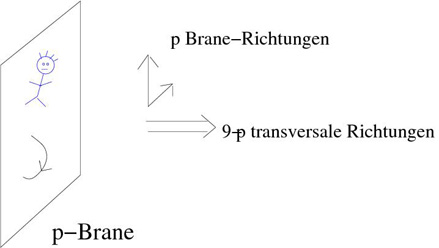
Abb. 3: p-Brane mit einem offenen String.

Eine Bewegung transversal zur p-Brane ist für die Teilchen des Standardmodells unmöglich. Deswegen können die extra Dimensionen in den transversalen Richtungen auch viel größer als nur 10^-16 cm sein, die experimentellen Schranken betragen hier nur einige Mikrometer (siehe unten). Trotzdem verlieren die extra Dimensionen nicht gänzlich Einfluss auf die drei-dimensionale Welt, da die Kraftteilchen der Gravitation, nämlich die Gravitonen, als die niedrigste Anregungsmode des geschlossenen Strings erscheinen. Im Gegensatz zum offenen String kann der geschlossene String aber in alle neun Raumrichtungen propagieren. Experimentell bedeutet dies, dass sich u.U. bei sehr kurzen Abständen im Bereich von Distanzen, die kürrzer als ca. 10^-5 Meter sind, Abweichungen vom Newtonpotenzial der Gravitationstheorie ergeben könnten, die von dem Eintreten der Gravitonen in die extra Dimensionen herrühren.

In der Abteilung Stringtheorie am Max-Planck-Institut für Physik werden nun verschiedene Aspekte von Brane-Welten untersucht. Im Vordergrund der Diskussion steht dabei die Frage, ob man auf diese Art und Weise aus der Stringtheorie das supersymmetrische Standardmodell der Elementarteilchenphysik (kurz als MSSM bezeichnet) herleiten kann. Dabei hat sich herausgestellt [1], dass Brane-Welten, in denen die p-Branen einerseits vollständig das gesamte drei-dimensionale Universum ausfüllen, aber sich andererseits in einen Teil des zusätzlichen, kompakten 6-dimensionalen Raumes erstrecken und sich dort auch schneiden können, besonders gut geeignet sind, um das MSSM zu reproduzieren. Man nennt diese Stringmodelle deswegen auch „intersecting branes“ (Abb. 4).

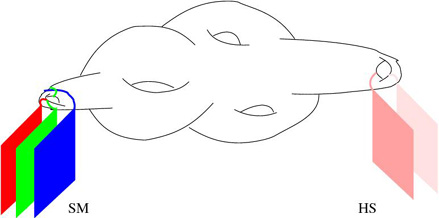
Abb. 4: Standardmodell und versteckte (hidden) p-Branen, die sich im internen Raum schneiden.

Die Quarks und Leptonen des MSSM entsprechen dabei offenen Strings, die an den Schnittpunkten der p-Branen im inneren Raum lokalisiert sind. Neben diesen brane-Welt-Modellen werden am Max-Planck-Institut aber auch andere, oft duale Stringkompaktifizierungen mit so genannten
magnetischen Flüssen studiert [2].

Ein interessanter Aspekt der intersecting brane-Welt-Modelle ist, dass man in ihnen auch das Phänomen der Supersymmetriebrechung konkret berechnen kann [3], welches für die Massen der supersymmetrischen Partnerteilchen verantwortlich ist. Dies ist sicherlich auch für die zukünftigen Experimente am LHC in Genf von Wichtigkeit. Die Supersymmetriebrechung geschieht dadurch, dass die Supersymmetrie durch bestimmte „magnetische“ Flussfeldstärken, die im internen Raum liegen, gebrochen wird. Diese so genannten Hintergrundsflüsse haben ferner die weitere wichtige Eigenschaft, dass durch sie viele der ansonsten unbestimmten geometrischen Parameter (sog. Modulifelder) auf einen festen Wert eingefroren werden [4]. Auf diese Art und Weise erhält der innere Kompaktifizierungsraum ein starres, festes Aussehen, welches man nicht mehr durch die Deformation der geometrischen Modulifelder verändern kann. Das „Einfrieren“ der Modulifelder zieht zahlreiche phänomenologisch erwünschte Vorteile nach sich, wie etwa die Abwesenheit von zusätzlichen Kräften (sog. 5th. force) in der Natur, die durch masselose Modulifelder verursacht werden, oder auch die prinzipielle Berechenbarkeit von zahlreichen Kopplungen im Standardmodell, wie auch die Massen der supersymmetrischen Partnerteilchen [5]. Ferner hat der Mechanismus der Modulistabilisierung auch einschneidende Konsequenzen in der Kosmologie, wie etwa eine mögliche stringtheoretische Erklärung der dunklen Energie des Universums, welche Einstein als kosmologische Konstante in seine Gravitationsformel eingeführt hatte. Schließlich, wie schon seit langer Zeit bekannt ist, ist die Anzahl der möglichen Stringkompatifizierungen riesig groß, von der Größenordnung 10^500-1000 oder mehr. Deswegen spricht man in diesem Zusammenhang auch von der sog. Stringlandschaft, und man versucht statistische Aussagen über die Verteilung der physikalischen Parameter in der Stringlandschaft zu erlangen [6].

Diese und viele andere physikalische und phänomenlogische Aspekte waren der Gegenstand der internationalen Konferenz „String Phenomenology 2005“, die gemeinsam vom Max-Planck-Institut für Physik und vom Arnold-Sommerfeld-Zentrum für theoretische Physik vom 13.-18. Juni 2005 an der LMU-München durchgeführt wurde sowie des workshops „The string vacuum workshop“, 22.-24.Nov.2004 am MPI für Physik.
Es muss dabei herausgehoben werden, dass es in der Stringtheorie noch eine große Anzahl von ungelösten Problemen gibt, die sowohl prinzipieller Natur sind, insbesondere was die Struktur von Raum und Zeit bei sehr kurzen Abständen in der Nähe der Planck'schen Skala angeht, als auch was die Herleitung des MSSM aus der Stringtheorie betrifft. Insbesondere gibt es bis heute noch kein Stringmodell, das alle Eigenschaften des MSSM vollkommen richtig beschreibt und erklärt.

2.) Äquivalenz von Quanten- und Relativitätstheorie - die AdS/CFT-
Korrespondenz

Konforme Feldtheorien (CFT) sind von wichtiger Bedeutung in der theoretischen Physik. Punktförmige Teilchen und ihre Wechselwirkungen werden allgemein durch Felder beschrieben. Konforme Feldtheorien sind spezielle Feldtheorien, die einen besonders hohen Symmetriegrad aufweisen, da sie unter konformen Koordinatentransformationen invariant sind. Sie lassen sich insbesondere im Zusammenhang mit den Fragestellungen der Vereinheitlichung der Wechselwirkungen und der Auswirkungen der Stringtheorie auf die Elementarteilchenphysik als Anschauungsbeispiele verwenden.

Bei einer konformen Koordinatentransformation kann sich nicht nur wie bei der Rotation die Lage eines Gebiets im Raum verändern, sondern auch seine Größe und Form, allerdings in einer ganz bestimmten Weise: An jedem einzelnen Punkt ist die Symmetrietransformation winkeltreu. Ein Beispiel für eine konforme Transformation ist in Abbildung 5 zu sehen. Dort werden die Punkte innerhalb des Dreiecks links mit einer konformen Transformation auf die Fläche rechts abgebildet. Insbesondere wird der rechte Schenkel des Dreiecks, blau eingezeichnet, auf den oberen Rand der Fläche rechts, ebenfalls blau eingezeichnet, abgebildet. Ebenso wird der rote linke Schenkel des Dreiecks auf den unteren roten Rand der Fläche rechts abgebildet. Die übrigen roten und blauen Strecken im Inneren des Dreiecks links werden jeweils paarweise auf die roten und blauen Kurven im Inneren der Fläche rechts abgebildet. Gut zu erkennen ist, dass die geraden Strecken links durch die Abbildung zu Parabeln werden.

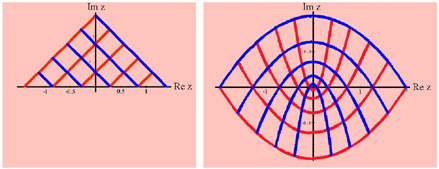
Abb. 5: Konforme Koordinatentransformation.

Zwar beschreiben konforme Feldtheorien die Modelle der Elementarteilchenphysik nur in bestimmten Grenzfällen. Aufgrund ihrer lösbaren mathematischen Struktur lassen sich jedoch für diese Theorien Fragen klären, deren Beantwortung für realistische Modelle zunächst zu schwierig wäre. Die Strategie ist, die für konforme Feldtheorien gefundenen Ergebnisse anschließend auf die realistischen Modelle zu verallgemeinern.

1997 wurde von Juan Maldacena eine wichtige Äquivalenz zwischen einer konformen Quantenfeldtheorie und einer Gravitationstheorie, d.h. einem bestimmten Modell der Relativitätstheorie entdeckt. Diese als dS/CFT-Korrespondenz bezeichnete Äquivalenz erhielt er aus der Untersuchung des niederenergetischen Grenzfalls eines Modells der Membranentheorie. „AdS“ steht für den - nach dem niederländischen Physiker Willem de Sitter benannten - Anti-de-Sitter-Raum, also für die Gravitationstheorie. „CFT“ ist die Abkürzung für konforme Feldtheorie. Bemerkenswert ist an der AdS/CFT-Korrespondenz, dass erstmals ein Zusammenhang zwischen der Quantentheorie einerseits und der klassischen Relativitätstheorie andererseits hergestellt wird. In der AdS/CFT-Korrespondenz hat man damit zwei unterschiedliche Theorien, die dasselbe physikalische Phänomen beschreiben. Dies ermöglicht die Berechnung identischer physikalischer Observablen auf zwei unterschiedliche Weisen. Deswegen erhofft man sich, dass man unter Ausnutzung der AdS/CFT-Dualität nicht-störungstheoretische Phänome in Eichtheorien, wie z.B. das Confinement in der QCD als Theorie der starken Wechselwirkung, berechnen kann, indem man entsprechende Größen in der dualen, aber klassischen gravitationstheorie betrachtet.

Ein wesentliches Merkmal der AdS/CFT-Korrespondenz ist, dass ein Modell der Quantentheorie in vier Raum-Zeit-Dimensionen und ein Modell der klassischen Relativitätstheorie in fünf Dimensionen, also in einer Dimension mehr, zueinander in Beziehung gesetzt werden. Dies wird auch als holographisches Prinzip bezeichnet.
In Abbildung 6 ist die AdS/CFT-Korrespondenz dargestellt. Man sieht eine zweidimensionale kreisförmige Fläche, die unsere vierdimensionale, flache (nicht gekrümmte) Raumzeit symbolisiert. Diese wird als Minkowski-Raum bezeichnet. In diesem Raum laufen physikalischeProzesse nach den Gesetzen der Quantenphysik ab. Gleichzeitig ist diese Fläche der Rand eines gekrümmten Raums von hyperbolischer Form, der als Anti-de Sitter-Raum bezeichnet wird. In diesem Raum unterliegen physikalische Prozesse den Gesetzen der klassischen Relativitätstheorie. Der Raum der Relativitätstheorie hat eine Dimension mehr als der Raum der Quantentheorie. Diese zusätzliche Dimension wird als holographische Dimension bezeichnet, da die AdS/CFT-Korrespondenz einem Hologramm ähnelt, bei dem eine zweidimensionale Abbildung ein dreidimensionales Bild erzeugt. Ebenso sind bei der AdS/CFT-Korrespondenz der Informationsgehalt der vierdimensionalen und der fünfdimensionalen Theorie gleich. In Abbildung 6 ist als physikalischer Prozess die Bewegung eines Teilchens von A nach B gezeigt, wobei die Punkte A und B im Minkowski-Raum und damit gleichzeitig auf dem Rand des Anti-de Sitter-Raums liegen. Die AdS/CFT-Korrespondenz besagt, dass die
Bewegung innerhalb des Minkowski-Raums, die nach den Gesetzen der Quantentheorie erfolgt und mit der blauen Schlangenlinie dargestellt ist, äquivalent ist zur klassischen Bewegung entlang der roten Kurve durch den Anti-de Sitter-Raum, die nach den Gesetzen der Relativitätstheorie erfolgt. In einigen Spezialfällen ist es sogar so, dass die beiden unterschiedlichen Beschreibungen der physikalischen Prozesse und Observablen auch numerisch exakt denselben Wert liefern.

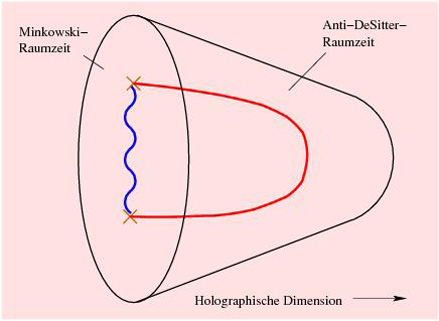
Abb. 6: AdS/CFT-Korrespondenz.

Die Forschungsprojekte am Max-Planck-Institut zielen darauf, die AdS/CFT-Korrespondenz in verschiedener Hinsicht zu erweitern und zu verallgemeinern. Es wird daran geforscht, die Korrespondenz so zu erweitern, dass sie nicht nur für quantentheoretische Modelle mit konformer Symmetrie, sondern auch für die drei Wechselwirkungen der Elementarteilchenphysik gilt. Dazu muss insbesondere der Symmetriegehalt reduziert werden. Auf der quantentheoretischen Seite der Korrespondenz weicht man daher von den konformen Feldtheorien ab und wendet sich allgemeineren Quantenfeldtheorien (QFT) zu, die denen der Elementarteilchenphysik verwandt sind. Dem entspricht auf der Relativitätstheorie-Seite der Korrespondenz, dass der hyperbolische Anti-de Sitter-Raum in Abbildung 3 deformiert werden muss. Es wird folglich an einer „deformed AdS/QFT“-Korrespondenz gearbeitet.

Als weiteren Schritt in Hinblick auf die Elementarteilchenphysik haben wir kürzlich Ergebnisse veröffentlicht, mit denen sich mit der AdS/CFT-Korrespondenz in der Quantentheorie Quarks beschreiben lassen, die Bausteine der Protonen, Neutronen und Mesonen. Dazu werden p-Branen in den Anti-de Sitter-Raum gelegt. Damit ist es uns gelungen, eine Gravitationsbeschreibung von Niederenergiephänomenen in der Theorie der starken Wechselwirkung zu liefern. Ein Beispiel dafür sind die chirale Symmetriebrechung und die leichten Massen einiger Mesonen [7]. Weiterhin konnten wir mit ähnlichen Verallgemeinerungen der AdS/CFT-Korrespondenz einen neuen Phasenübergang in Quantenfeldtheorien bei endlicher Temperatur vorhersagen [8]. Ein weiterer Aspekt ist die Einordnung der verallgemeinerten AdS/CFT-Korrespondenz in die Stringtheorie - bisher ist diese Korrespondenz nur für den niederenergetische Grenzfall der Stringtheorie formuliert. In diesem Zusammenhang konnten wir einige offene Fragen klären [9].

Eine Beantwortung dieser faszinierenden Fragen der Grundlagenforschung wird viel zu einem besseren Verständnis der Materie und ihrer Wechselwirkungen beitragen. Es soll jedoch auch erwähnt werden, dass die dabei entwickelten Methoden, insbesondere die Verwendung der konformen Symmetrie, auch in anderen Bereichen der Physik Anwendung finden können, zum Beispiel in der Festkörperphysik bei der Beschreibung magnetischer Systeme. Dies ist ein weiteres Beispiel dafür, dass die Grundlagenforschung einen wichtigen Motor der Forschung insgesamt darstellt.