wiese-hkg

Lothar Wiese A. Butorac 1 HR 52440 Porec und Teheranski trg 7 BiH 71000 Sarajevo, 01/2003-09/2004, erstes unkorrigiertes Konzept

Stoßverhalten in einem idealen Gas harter Kugeln (HKG)

In Anlehnung an die in " Struktur und Dynamik der Materie im Uratommodell " vorgestellte Idee zur Untersuchung von harten Kugeln als Alternative zu Strings, Superstrings oder Branes wird ein einfaches Gas gemäß folgender Annahme näher untersucht:
Es existiert einzig und allein eine Menge abzählbar unendlich vieler, sich im 3-dimensionalen Raum bewegender, gleich großer fester Kugeln. Diese durchdringen den leeren Raum geradlinig. Eine Annäherung an eine andere Kugel erfolgt bis zum Zusammenstoß (Berührung), bei dem nur die Geschwindigkeitskomponenten in Richtung der Stoßachse (Berührungsnormale) ausgetauscht werden. Das entspricht dem einfachen Fall gleich schwerer idealer Kugeln, deren Masse 1 weggelassen werden kann.
Aus dieser Hypothese folgt direkt, dass alle physikalischen Systembildungen, Symmetrien, Wechselwirkungen,... und damit alle Naturgesetze auf die Selbstwechselwirkungen, also Stöße, zurückzuführen sein müssen. Bei diesen bleiben Energie und Impuls erhalten.

1. Definitionen

Im betrachteten harte Kugeln Gas (HKG) soll zumindest anfangs davon ausgegangen werden, dass alle n Ausgangsorte homogen im dreidimensionalen Raum, also gleichverteilt, vorkommen. Alle Flugrichtungen seien wegen der Isotropie ebenfalls gleichwahrscheinlich. Parallele Flugbahnen mit durchschnittlich gleichen Abständen voneinander sind ebenfalls zulässig (rot). Bewegte Kugeln mit festem Durchmesser d müssen zwangsweise irgendwann zu Stößen führen. Zum Zeitpunkt des gegenseitigen Berührens bildet die Relativgeschwindigkeit (dick rot) die z-Richtung eines Koordinatensystems. Relativ zu dieser ist die Stoßachse (Berührpunktnormale) auf der Kugel mit dem Durchmesser 2 d durch den Stoßachsenwinkel f und den frei wählbaren Winkel q (leider hier vertauscht, siehe Definitionen) definiert.

Bild_1

Für den Winkel q gilt wegen der Symmetrie der Drehung um die Relativgeschwindigkeit, dass dieser im vollen Kreis mit der Wahrscheinlichkeitsdichte 1 / 2 p gleichverteilt ist. Deshalb ergibt sich als Zufallsgenerator:

(1)

Für den wichtigen Öffnungswinkel f, welcher der eigentliche Stoßachsenwinkel ist, muss nun die Gleichverteilung von möglichen Flugbahnen auf der zum Relativgeschwindigkeitsvektor orthogonalen Kreisfläche berücksichtigt werden. Erreicht wird das durch die Zuordnung von

(2)

Diese leitet sich einfach aus dem Zusammenhang:

das von 0 bis p/2 monoton wächst und deshalb Verteilungsfunktion ist, her. Es wird demnach:

, woraus (2) folgt.

Das ist eine angepasste Zufallsverteilung auf dem Durchmesser, die mit dem Winkel q beliebig gedreht werden kann. Beispielsweise mit

ergibt sich für die Verteilung der Stoßachsenwinkel auf der Kugeloberfläche,
bzw. mit s für die Flugbahnen in der Kreisebene, also mit:

Bild_2

Bild_3

Bei Zusammenstößen ist darüberhinaus interessant, auf welche Art der Relativgeschwindigkeitsvektor w gebildet wurde. Die ursprünglichen beiden Vektoren v und u können einen Winkel zueinander bilden. Dieser ist von der Bewegung des gewählten Koordinatensystems abhängig. Einer der beiden Stoßpartner (hier u) kann deshalb mit seiner Bewegung in x-Richtung gelegt werden. Bei der Bildung der Relativgeschwindigkeit bleibt diese Richtung im Laborsystem erhalten. Der Flugwinkel b (zwischen v und u) gilt wie der Winkel F der Relativgeschwindigkeit w im System der mit u (Geschwindigkeitsbetrag) bewegten Kugel.

Bild_4

Gemäß der Skizze seien:

(3)

und damit:

also

(4)

Das betrachtete HKG wird durch n Teilchenorte und n Teilchengeschwindigkeiten beschrieben. Mit einem Zeitparameter t lassen sich demnach alle Teilchenorte zu einem beliebigen Zeitpunkt t bestimmen.
Darüber hinaus soll das HKG noch eingebettet in eine Umgebung gedacht werden, welche ebenfalls durch ein HKG gebildet wird. Dessen Eigenschaften sollen nur in Form von Parametern zugrunde gelegter Zufallsverteilungen bekannt sein. Die Wechselwirkungen in Form von Stößen müssen deshalb durch Zufallsgeneratoren erzeugt werden.

Zusammengefasst werden in den erforderlichen Untersuchungen anfangs folgende Definitionen verwendet:
Es wird ein Koordinatensystem betrachtet, das mit u in x-Richtung sowie seiner z-Richtung in der Ebene von u und v, Richtung - v liegt. Zur Vereinfachung wird gemäß Bild 4 ein Stoßbereich mit doppeltem Durchmesser definiert, so dass alle anderen Teilchen als punktförmig angenommen werden können:

d Durchmesser der stoßenden Kugeln
L (durchschnittliche) freie Weglänge bis zum nächsten Stoß
u Geschwindigkeit des im Ursprung startenden Teilchens
v Geschwindigkeit des Stoßpartners
w Relativgeschwindigkeit v - u
b Winkel zwischen -v und u, also Flugwinkel
Q Herkunftswinkel der Relativgeschwindigkeit = Kollisionswinkel
Q Drehwinkel der Relativgeschwindigkeit um u,
verschwindet bei sinnvoller Drehung der z-Achse in Ebene mit v
f Stoßachsenwinkel (Winkel der Berührpunktnormale) erzeugt bzgl. Relativgeschw.
q Drehwinkel der Stoßachse orthogonal um Relativgeschwindigkeit
t Parameter der kontinuierlichen Zeit.

Als Vereinbarung soll darüber hinaus gelten, dass sich die Werte der obigen Winkel und Vektoren, wenn sie in Verbindung mit dem Index der Teilchennumerierung vorkommen, im Bedarfsfall auf ein festes Koordinatensystem (Laborsystem) beziehen und deshalb in dessen Werte umgerechnet werden müssen.

2. Stoßhäufigkeit

2.1 Grundsätzliches

Nach Bild 4 wird deutlich, dass es zu einem Stoß nur kommen kann, wenn der Relativgeschwindigkeitsvektor in Richtung der Kugel mit dem Radius 2 d zeigt, welche mit einem gedachten ruhenden Stoßpartner gebildet wird (vgl. unten).

In der Ausgangssituation soll vorerst ein Medium betrachtet werden, bei dem die Anzahldichte gleich verteilt und die vorkommenden Geschwindigkeiten normal verteilt sind. Die Wahrscheinlichkeitsdichten ergeben sich dabei nach den geometrischen Grundüberlegungen der Wahrscheinlichkeitsrechnung und führen zu den bekannten Maxwellschen Verteilungsfunktionen. Außerdem sei ein festes Koordinatensystem so gewählt, dass die räumlichen Koordinaten und die Zeit reell sind und orthogonal zueinander stehen. Die x- oder 1-Achse liege in der Richtung einer willkürlich ausgewählten Probekugel, welche sich gerade mit Durchschnittsgeschwindigkeit in positiver Richtung bewegt. Ihr Durchmesser sei 2 d, weil damit alle für einen Stoß in Frage kommenden Kugeln als Punkte angesehen werden können. Die Anfangsorte der Probekugel liegen in einem Zylinder mit gleicher Wahrscheinlichkeit an jedem Ort und die aller durch Punkte dargestellten Kugeln demnach in einem Volumen, welches nur durch die maximale Geschwindigkeit beschränkt ist und das vom Anzahldichte- Erwartungswert bestimmt wird. Der Einfachheit halber wird hier der Zusammenhang verwendet, dass die durchschnittliche freie Weglänge L mit der Anzahldichte n und dem Durchmesser d folgendermaßen bestimmt ist:

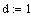
wird als willkürliche Maßeinheit der Länge gewählt.

(5)

(6)

Dieser Zusammenhang entsteht durch eine gedachte Verschiebung aller Kugeln in eine voll aufgefüllte Ebene wie in der kinetischen Gastheorie. Damit gilt dann für die absolute Zusammenstoßhäufigkeit (Stoßfrequenz):

(7)

Die Relativgeschwindigkeit ist nach Bild 4 durch

(8)

definiert.

Die sich ergebenden Relativgeschwindigkeiten (rot), auf eine bewegte Kugel zu und von einem etwa gleich weit entfernten Bereich um dieses Probeteilchen herum mit jeweils gleichem Geschwindigkeitsbetrag eines Stoßpartners, sind in Bild 5 zu erkennen.

Bild_5

Seien nun verschiedene u beliebige in dem betrachteten HKG zulässige Geschwindigkeitsbeträge eines Probeteilchens und v der Geschwindigkeitsbetrag von möglichen Stoßpartnern. Dann gilt:

(9)

(10)

Womit sich beliebige Relativgeschwindigkeiten ermitteln lassen, z.B.:

Mit

lassen sich nun die Relativgeschwindigkeitsbeträge abhängig vom

Flugwinkel b auch grafisch darstellen, z.B. mit Durchschnittsgeschwindigkeitsbetrag:

Bild_6

Aus dem Zusammenhang zwischen Herkunfts- = Kollisionswinkel F und Flugwinkel b lässt sich wie aus Bild 4 ersichtlich auch deren Zuordnung zu den Relativgeschwindigkeitsbeträgen bilden:

(11)

(12)

Diese können wiederum grafisch dargestellt werden (Bild 7) und zeigen die vermutete Asymmetrie.

Bild_7

2.2 Bedingte Stoßfrequenzdichte für ein bewegtes Teilchen

Interessant ist hier vor allem die Abhängigkeit der sich ergebenden Kollisionswinkel F von den Relativgeschwindigkeitsverteilungen, welche vorerst vereinfacht unabhängig von diesen als standard-normal, also N(0,1) verteilt, angenommen werden sollen. Die bedingte Wahrscheinlichkeitsdichte für das Auftreffen eines Punktes aus einem bestimmten Winkel auf die betrachtete Probekugel ergibt sich deshalb aus dem Produkt der beiden Wahrscheinlichkeitsdichten mit der verschobenen Verteilung der Relativgeschwindigkeit (vgl. Brendel_phi.pdf). Das drückt sich in den hier (aus Symmetriegründen vorerst) interessierenden zwei Dimensionen durch die vereinfachte Wahrscheinlichkeitsdichte:

(13)

aus,

woraus mit u in x-Richtung folgt:

(14)

was sich in Polarform

(15)

schreibt.

Das erste Moment (Mittel- oder Erwartungswert) dieser Funktion liefert die bedingte Frequenz von Stößen aus der Richtung F auf ein mit dem Geschwindigkeitsbetrag u fliegendes Teilchen. Um in der grafischen Darstellung einen den Bildern 4 und 5 entsprechenden Eindruck zu erzielen, dass die von rechts kommenden Kugeln häufiger treffen, könnte ein Faktor -1 eingefügt werden.

(16)

Deren graphische Darstellung bereitet kein Problem:

Bild_8

Die Abhängigkeit der Stoßfrequenz vom Flugwinkel b lässt sich ebenfalls mit (16) grafisch darstellen, indem dort anstelle F das abhängige F(u,b) eingesetzt wird:

(17)

(18)

Bild_9

Aus den Bildern 8 und 9 wird die vermutete Asymmetrie der Stoßfrequenz in Abhängigkeit von den Winkeln F bzw. b deutlich. Sie ist viel größer als bei der reinen Betrachtung der Relativgeschwindigkeiten ohne Berücksichtigung der Geschwindigkeitsverteilungen. Von vorn treffen die Probekugel mehr Teilchen als von der Seite oder von hinten. Für b bei großen u ergibt sich eine Anschmiegung der F(u,b) und deshalb eine erneute Abnahme der Stoßfrequenzdichte.

Bild_10

Zur Verwendung als Zufallsgenerator wird jetzt versuchsweise w(u,F) = 0 gesetzt:

(19)

Eine Auflösung nach F gelang leider nicht.

Das Integral für beliebige u lässt sich aber ermitteln, z.B:

(20)

Bei der Mittelung über alle Geschwindigkeiten u

(21)

gelingt im verwendeten Computeralgebrasystem (CAS) die Umformung nur bis:

(22)

und

(23)

ist nach Brendel_stoss.pdf noch eine mögliche Vereinfachung.

Wegen der einbezogenen vom Winkel unabhängigen Geschwindigkeitsverteilung, hier repräsentiert von der Durchschnittsgeschwindigkeit, lässt sich aber der Zufallsgenerator für F denken. Zuerst muss folgendes Integral ermittelt werden:

(24)

Wird das ursprüngliche nicht vereinfachte Integral (22) verwendet, ermittelt das CAS den gleichen Wert, was die Vereinfachung bestätigt. Damit wird

und

(25)

Zur Probe die Funktionswerte an einigen Stellen:

F(F) ist also Verteilungsfunktion und f(F) Wahrscheinlichkeitsdichte, was numerisch und graphisch nachvollzogen werden kann:

Bild_11

Jedem Wert zwischen 0 und 1, welcher zufällig durch rnd(1) erzeugt werden kann, muss demnach eindeutig ein Winkel f zuordenbar sein. Die symbolische Integration von:

(26)

gelingt allerdings wiederum nicht mit Mathcad. Eine Auflösungsmöglichkeit nach F und Verwendung als Zufallsgenerator für dieses ist nicht zu erkennen.

Weil aber der Zufallsgenerator n zufällig gemäß einer gegebenen Verteilungsfunktion verteilte Zahlen liefern soll, kann die unnötige Auflösung übersprungen und gleich ein Verfahren zur numerischen Lösung eingesetzt werden. Sei beispielsweise obiges F(F) gegeben, wird dies mit rnd(1) als implizite Funktion FG ausgedrückt:

(27)

und zur Nullstellenbestimmung die Lösungsmenge mit einer Näherungslösung aus dem zulässigen Intervall initiiert:

sowie dann die root-Funktion verwendet:

(28)

Auf diese Art lassen sich beispielsweise auch n solche Zahlen F ermitteln:

(29)

Diese Winkel sind jedoch von der durchschnittlichen Geschwindigkeit beeinflusst. Hieraus lassen sich mit w(u,F) auch Wertepaare zufälliger Geschwindigkeitsbeträge mit zufälligem Kollisionswinkel F erzeugen. Dazu muss aber erst die Normierung von w überprüft werden. Dann sind n zufällige Geschwindigkeitsbeträge beispielsweise mit rnorm(n,a,s) zu erzeugen und mit diesen ist jeweils w zu normieren und dann ein zugehöriges F zu generieren. Wegen der angenommenen Unabhängigkeit des Geschwindigkeitsbetrags v von der Richtung F kann nun wiederum mit rnorm(n,a,s) zu jedem Paar (u,F) das zugehörige (v,b) errechnet werden.

2.3 Abhängigkeit der Stoßfrequenz vom Flugwinkel b

Zuerst werden zufällige Vektoren u erzeugt, bei welchen aber wegen des vorläufig verwendeten rnorm(n,a,s) darauf geachtet werden muss, dass diese nicht negativ werden. Die F werden von oben genommen:

(30)

Deren tabellarische Anordnung erfolgt nur übersichtshalber

Ähnliches erfolgt für v und die neue Tabelle:

(31)

Laut Bild 4 wird b :

(32)

und damit werden

(33)

die gewünschten Vektoren mit deutlich zu erkennender Häufung um p, also häufigen Frontalstößen.

Noch nützlicher wäre allerdings ein Zufallsgenerator ohne explizite Kenntnis einer Wahrscheinlichkeitsverteilung, nur auf der Basis einer bekannten Menge sich bewegender Kugeln. Die kontinuierlichen Zwischenwerte müssten dann durch Interpolation gewonnen werden.
Unberücksichtigt ist bisher auch die Möglichkeit, dass keine Standardnormalverteilung bzw. Maxwellverteilung zugrunde gelegt werden darf, sondern eine N(1,s)-Verteilung der Geschwindigkeitsbeträge bzw. gar eine "tatsächliche" noch unbekannte Geschwindigkeitsverteilung. Auch sollte die spätere Simulation von Stößen noch die Anzahldichte r bzw. d/L und einen damit bestimmbaren Zeitfaktor für den nächsten Stoß, berücksichtigen (vgl. (10)).
Der Einfluß einer möglichen variablen Geschwindigkeitsstreuung wurde in der Frontalstoßbeweisidee zwar anfangs angenommen, später aber durch den Einfluß von Brendel_beta.pdf in betavert.htm verworfen (Flugwinkeluntersuchungen mit Stoßkegel). Der Widerspruch bei den unterschiedlichen Vorgehensweisen ist durch obige Erzeugung von Häufungen um "Frontalstöße" noch nicht ganz ausgeräumt. Die Unabhängigkeit der Stoßfrequenz vom Flugwinkel b gilt ja nur bei der verworfenen alten Vorgehensweise vom Stoßkegel aus, wo einfach der Versuch mit einem Stoßpartner vielfach wiederholt wurde. Deshalb soll nochmals bei der Ausgangssituation zur Ermittlung einer Wahrscheinlichkeitsdichte für die Stoßfrequenz begonnen werden.

2.4 Konstruktion einer Stoßfrequenz-Wahrscheinlichkeitsdichte

Ausgegangen wird von einer als bekannt vorausgesetzten Wahrscheinlichkeitsdichte für die Geschwindigkeit, welche hier erst einmal einer N(a,s)-Verteilung mit Werten von v > 0 zugeordnet sein soll. Die Parameter sollen noch willkürlich gewählt werden, um nicht von vornherein die Maxwellverteilung zu präjudizieren:

und der Wahrscheinlichkeitsdichte für den Flugwinkel

Damit ergibt sich die zweidimensionale Wahrscheinlichkeitsdichte für das "Fliegen" eines Teilchens:

(34)

mit

für kleine s (bei großen gibt es Bereichsüberschneidungen)

In kartesischen Koordinaten wird daraus:

mit

(35)

und der daraus folgenden Funktionaldeterminante für die Koordinatentransformation:

(36)

also

(37)

(38)

was sich wieder leicht grafisch darstellen lässt und gut die gewünschte Wahrscheinlichkeitsdichte veranschaulicht:

Bild_12

Mit dieser Wahrscheinlichkeitsdichte lässt sich nur die Wahrscheinlichkeit für das Vorkommen einer Geschwindigkeit in der (aus Symmetriegründen) betrachteten Ebene ermitteln. Nun soll aber ein zweites Teilchen mit diesem zusammenstoßen.

Das Vorkommen von zwei zufälligen Geschwindigkeiten und des zufälligen Flugwinkels b der beiden Geschwindigkeiten zueinander, in der aus Symmetriegründen betrachteten Ebene, ist unabhängig voneinander. Deshalb kann die Dichte f(u,v,b), die sich aus dem Produkt der Einzeldichten ergibt, verwendet werden.

(39)

Die enthaltenen Dichten, nur umgestellt, ergeben die Wahrscheinlichkeitsdichte:

(40)

In dieser Form hilft diese Wahrscheinlichkeitsdichte hier aber nicht weiter, weil nur das sowieso bekannte in allen Raumrichtungen homogen verteilte Fliegen der Teilchen betrachtet wird. Außerdem nicht mit berücksichtigt ist in dieser Wahrscheinlichkeitsdichte der mögliche Einfluss unterschiedlicher freier Weglängen der beteiligten Teilchen auf das Zusammentreffen zur gleichen Zeit am gleichen Ort. Ausgedrückt werden kann das durch die freie Weglänge L oder die Anzahldichte n, bei festem Teilchendurchmesser d. Deshalb wird erst einmal eine unabhängige Wahrscheinlichkeitsdichte für n oder L gesucht.

Allgemein wird in der Thermodynamik zur Herleitung der Maxwellschen Geschwindigkeitsverteilung meist von einem kanonischen Ensemble und dessen Verteilungsfunktionen ausgegangen. Maxwell selbst ging von der Annahme aus, dass die gesuchte dreidimensionale Wahrscheinlichkeitsdichte aus dem Produkt der Randdichten gebildet wird und dass sie eine Funktion der kinetischen Energie der Teilchen ist. Obwohl die Abhängigkeit vom Ortsvektor meist weggelassen werden kann, wird dieser doch für die Normierung dadurch verwendet, dass die Integration über die zulässigen Geschwindigkeiten und das betrachtete Volumen V gerade die Teilchenzahl N in diesem Volumen ergeben muss. Dabei gilt n = N / V mit 0 < N < 1. Im betrachteten einfachen HKG wird die Teilchenanwesenheit aber als gleichmäßig verteilt angenommen und deshalb können die Parameter der Anzahldichte vorerst weggelassen werden. Richtungsabhängige Geschwindigkeits- und Anzahldichteasymmetrien werden vorerst als lokal unabhängig von Nachbarpunkten angenommen. Für die Wahrscheinlichkeitsdichte der Stoßfrequenz in Abhängigkeit von den Flugwinkeln folgt deshalb
beim Interesse an der reinen Geschwindigkeitsverteilung, dass alle überflüssigen Größen möglichst eliminiert werden sollen. So fällt die Abhängigkeit von n durch die Normierung gleich wieder weg, wenn das Interesse sich auf die Winkelabhängigkeit bezieht.
Wird nun angenommen, dass die Geschwindigkeiten jeweils N(a,s) verteilt sind, ergibt sich die Stoßwahrscheinlichkeitsdichte aus dem Produkt der Dichten:

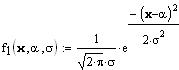
und

(41)

sowie

Die x und y sind aber noch Vektoren. Diese werden nun im Ruhsystem des Teilchens u betrachtet, wobei der erste Vektor durch Subtraktion von sich selbst verschwindet und für den zweiten steht v - u, also die Relativgeschwindigkeit. Die winkelabhängige Stoßfrequenz-Wahrscheinlichkeitsdichte wird deshalb einfach durch die Transformation der Dichte (40 ) in das mit einem Teilchen u mitbewegte Koordinatensystem eingeführt. Dabei ergibt sich im ersten Teil der obigen Dichte exp(u -u....) und im zweiten Teil exp(v - u ...), also die Relativgeschwindigkeit w.
In Abhängigkeit von b schreibt sich die Relativgeschwindigkeit als:

(42)

wobei zuerst eine Koordinatenverschiebung mit der Funktionaldeterminante 1und dann die Rücktransformation in polare Koordinaten mit der Funktionaldeterminante v durchgeführt wird. Die Relativgeschwindigkeit ist aber keine umkehrbar eindeutige Abbildung, weshalb nur die bedingte Wahrscheinlichkeit betrachtet wird. Damit ergibt sich:

(43)

wobei die Definition der neuen a und s noch offen gelassen wird.

Als Mittelwert über alle v folgt nun:

(44)

und mit beliebigem u, hier z.B. mit

ist (44) eine bedingte Wahrscheinlichkeitsdichte bei 0.04 < s < 0.35, welche für a = 0 und s = 1 der in Brendel_stoss.pdf (Gl. (33) und Abbildung 1) verwendeten Dichte für die Stoßfrequenz entspricht und den gleichen Zusammenhang wie mit (16) ergibt. Ungleich 1 wird dieses Integral durch Rechenungenaugkeiten sowie unzulässige vorkommende Geschwindigkeiten < 0 durch die zugrundegelegte Normalverteilung.

Es sei nun

und

Bild_13

Aus (44) kann ein bedingtes F(u,b) konstruiert werden, wobei sinnvollerweise a = 1 gesetzt wird, weil in dem vorerst betrachteten einfachen homogenen und dünnen HKG der Erwartungswert der Geschwindigkeit 1 ist. Die Funktion braucht nicht normiert zu werden, weil das Integral über f(u,b,1,s) gleich 1 ist für die interessierenden Geschwindigkeitsstreuungen.
Der Zufallsgenerator für b ergibt sich demnach einfach aus der impliziten Funktion mit

(45)

Mit einem anfänglichen b indiziert wird der Zufallsgenerator, wegen Rechenzeit- und Speicherbegrenzung hier nur zur Probe:

(46)

also

Auf gleiche Art muss sich nun allerdings auch der Zufallfgenerator unter den zwei Bedingungen, u und v konstruieren lassen, weil ja die beiden Geschwindigkeitsbeträge zufallsabhängig sind und es gleichgültig sein muss, ob diese vor oder nach der zufälligen Flugwinkelbestimmung bekannt sind. Es kann also direkt (43) verwendet werden:

mit beliebigen u und v sowie a und s ist

allerdings im Allgemeinen ungleich 1. Um das für den gesuchten Zufallsgenerator verwenden zu können, ist die Funktion für alle u und v zu normieren, woraus folgt:

(47)

Der Zufallsgenerator wird wieder durch die implizite Funktion für b definiert:

(48)

Zur Probe wird ein zufälliger Wert ermittelt, wobei auch ein willkürlicher Wert zur Initialisierung von b eingesetzt wird:

Durchläuft y_kverschiedene Werte, kann die Abhängigkeit von den einzelnen Variablen und Parametern auch grafisch dargestellt werden:

Bild_14

Mit b_zg(u,v,b,a,s,y) ist nun ein Zufallsgenerator für Stoßsimulationen bzw. eine implizite Funktion konstruiert, mit der eine analytische Untersuchung des Einflusses von Veränderungen der Parameter a und s möglich wird. Damit lässt sich testen, mit welcher Standardabweichung s die Maxwellsche Geschwindigkeitsverteilung bzw. eine entsprechende Normalverteilung als Grenzwert bei vielen Stößen herauskommt.
Vorher sollen aber erst einmal die Stoßvorgänge näher untersucht werden.

3. Stoßfälle

3.1 Stoßtransformationen (Die korrekten Transformationen siehe: Stosstransformationen.htm

Im normalen Raum ist keine Richtung vor der anderen ausgezeichnet. Beim Zusammenstoß wird wegen Unkenntnis irgendwelcher Gesetze nur die zur Stoßachse parallele Geschwindigkeit ausgetauscht. Stoßachsen können zufällig relativ zu den vorkommenden Vektorwinkeln erzeugt werden, wobei davon ausgegangen werden kann, dass parallele Flugbahnen gleichwahrscheinlich sind.
Der Geschwindigkeitsdifferenz-Erwartungswert bei vielen Zusammenstößen einfacher Kugeln soll untersucht werden.
Der stoßende Vektor v hat 3 Komponenten und die Anzahl der Repräsentanten u einer Umgebung, deren Geschwindigkeiten sich bei den Stößen ändern, beträgt n.

Für die Stoßachsenermittlung ist zuerst die Relativgeschwindigkeit erforderlich.

(49)

Die Richtung der Relativgeschwindigkeit wird mit der Kugelkoordinaten-Transformation ermittelt:

(50)

(51)

Die Stoßachsenwinkel ergeben sich zufallsabhängig, wobei gleichwahrscheinliche parallele Bahnen zur Relativgeschwindigkeit angenommen werden. Das ist auf gleichwahrscheinliche parallele Bahnen bei den Stoßpartnern zurückzuführen.

(52)

Aus diesen werden die Koordinaten des Stoßachsenvektors ermittelt.

(53)

(54)

Beim Stoß werden nun die zur Stoßachse parallelen Geschwindigkeiten der beiden beteiligten Kugeln ausgetauscht. Alle Vektoren sollen jedoch weiterhin im ursprünglichen Koordinatensystem betrachtet werden.

parallele Geschwindigkeiten

(55)

orthogonale Geschwindigkeiten

(56)

Geschwindigkeiten nach Stoß

(57)

Die Geschwindigkeiten nach dem Stoß werden mit (53) für zwei beteiligte harte Kugeln demnach aus den ursprünglichen dreidimensionalen Geschwindigkeiten v und u mit zufällig zu ermittelnden Stoßachsenwinkeln bestimmt. Für den Test dieser Transformation werden zuerst einige v und u aus einer Datei PSI.prn eingelesen (je 2 x 3 kartesische Geschwindigkeitskoordinaten):

Es gilt demnach:

und

(58)

Die Winkel b zwischen den Stoßvektoren u und v sind hier durch y vorgegeben.

(59)

Nun werden für die Stöße zufällige Stoßachsenwinkel ermittelt, wobei parallele Flugbahnen als gleichwahrscheinlich vorausgesetzt werden (vgl. Definitionen):

und

(60)

Damit lassen sich für alle i die neuen kartesischen Geschwindigkeitskomponenten nach dem Stoß ermitteln:

(61)

(62)

Auch die dabei durchlaufenen Einzelschritte lassen sich überprüfen:

(63)

(64)

was dann tatsächlich die für Einheitsvektoren notwendigen Beträge 1 ergibt:

Die Vektorbetragsdifferenzen betragen vor

(65)

bzw. nach dem Stoß:

(66)

Dagegen ist der Geschwindigkeitsdifferenzbetrag ( = Relativgeschwindigkeitsbetrag) unverändert:

(67)

3.2 Stöße mit variablen Winkeln

Anstelle zufälliger Stoßachsenwinkel lassen sich auch alle über die zulässigen Bereiche laufenden Winkel untersuchen. Zuerst erfolgt aber die Untersuchung des Einflusses unterschiedlicher Flugwinkel b.

Das erste Teilchen habe jeweils die Standardgeschwindigkeit, also

(68)

Die Stoßpartner sollen vorerst mit konstanter Länge, aber unterschiedlichem Flugwinkel b erzeugt werden, wozu Kugelkoordinaten-Transformationen verwendet werden, aber die Drehungen um die x-Achse aus Symmetriegründen wegfallen sollen:

x als Funktion von r, und b:

(69)

y als Funktion von r, a und b wird mit rotationssymmetrisch wegfallendem a:

= 0

(70)

z als Funktion von r, a und b wird mit rotationssymmetrisch wegfallendem a :

(71)

Damit wird

(72)

Zur Probe ein entgegen fliegendes Teilchen:

Nun kann auch v verschiedene Werte durchlaufen:

(73)

Mit jeweils einem festen Stoßachsenwinkel lassen sich für alle i die neuen kartesischen Geschwindigkeitskomponenten nach dem Stoß ermitteln. Der Winkel f wird dabei willkürlich für aussagefähige Diagramme weiter unten (Bild 15) durchgespielt, r und b werden noch weiter unten (Bild 16) für das ganze Dokument festgelegt:

und

sowie

(74)

ergibt die Vektoren v_s nach dem Stoß

bzw. u_s

(75)

Die Vektorbetragsdifferenzen betragen vor

(76)

bzw. nach dem Stoß

(77)

Dagegen ist wiederum der Geschwindigkeitsdifferenzbetrag ( = Relativgeschwindigkeitsbetrag) bei den einzelnen Stößen unverändert, wird aber mit wachsendem b kleiner:

(78)

(79)

Hier für das folgende Bild wird nun der einzelne Winkel f festgelegt. Die b_idurchlaufen Werte von p bis 2 p:

Bild 15

Das Bild der möglichen Veränderungen in Abhängigkeit der durchlaufenen Flugwinkel b zeigt, dass Form und Verlauf unabhängig vom gewählten Stoßachsenwinkel f sind . Deshalb sollen alternativ auch zwei gleichbleibende stoßende Vektoren bei verschiedenen Stoßachsenwinkeln betrachtet werden:

(80)

und mit (68) ergibt sich bei

und

(81)

also

Der Stoßachsenwinkel wird relativ zum vorn bestimmten Relativgeschwindigkeitsvektor (vgl. (48)) erzeugt, wobei i von 1 bis n läuft:

(82)

(83)

(84)

Die Vektorbetragsdifferenzen betragen vor:

(85)

bzw. nach dem Stoß:

(86)

Die Veränderungen der Geschwindigkeitsbetragssummen von jeweils zwei Stoßpartnern werden:

(87)

Die Annäherungsgeschwindigkeitbeträge sind hierbei alle gleich

(88)

(89)

ist hierbei wieder die unveränderliche Geschwindigkeitsdifferenzbetragsänderung nach dem Stoß. Zum Durchspielen verschiedener b, f und r Stoßachsenwinkel in der graphischen Darstellung der Resultate werden diese wegen der leichteren Veränderbarkeit erst hier für das ganze Dokument definiert:

Bild_16

Der Verlauf der Geschwindigkeitsänderungen beim Durchspielen verschiedener Kollisionswinkel f und Geschwindigkeitsbeträge vor dem Stoß kann hiermit gut verfolgt werden. Damit ergeben sich erste Gesetzmäßigkeiten bei den elementaren Ereignissen, also Stößen:

Die Geschwindigkeitssumme vor einem Stoß ist gleich der Summe nach dem Stoß, unabhängig vom Stoßachsenwinkel:

Das gleiche gilt dann für deren Beträge

(90)

Bei den Summen und Differenzen der einzelnen Geschwindigkeitsbeträge gibt es nach den Stößen aber im Allgemeinen Veränderungen, wie aus (82) und (83) deutlich wird.

Die Geschwindigkeits-Betrags-Summe (83) und damit der Wert der gestrichelten blauen Kurve Ss von Bild 15 ist dabei oft sogar größer als vor dem Stoß. Vor allem wird das sehr deutlich, wenn der Flugwinkel b1 bzw. b sehr klein gewählt wird, es sich also um Frontalstöße handelt.

Bei den Geschwindigkeits-Betrags-Differenzen (75), der roten Kurve in Bild 9, ist bei den häufigen Frontalstößen ein kleinerer Wert zu erwarten, als vor dem Stoß.

Der Relativgeschwindigkeitsbetrag (Annäherung) vor einem Stoß ist allerdings gleich dem nach einem beliebigen Stoß (Entfernung):

(91)

Daraus folgt nach Einführung von Elementarmassen, welche der Kugelanzahl zugeordnet werden, direkt die Gültigkeit des Impulserhaltungssatzes. Durch Stöße verändert sich der Gesamtimpuls nicht.
Auch für die gebildeten Quadrate gilt Ähnliches:

(92)

Die Relativgeschwindigkeitsquadrate vor einem Stoß sind gleich denen nach dem Stoß.

(93)

Daraus folgt (mit den Elementarmassen 1) direkt die Gültigkeit des Energieerhaltungssatzes. Durch Stöße verändert sich die Gesamtenergie nicht.
Die Erhaltung von Impuls und Energie folgt aus der Betrachtung der Relativgeschwindigkeiten, weil deren Beträge auch bei Stößen unveränderlich sind.

Als wichtige Aussage gilt außerdem:
Nach einem Stoß, bei dem die Geschwindigkeits-Betrags-Summe kleiner wird (Querstoß), nimmt die Anzahldichte zu, weil nach einem festen Zeitintervall die Entfernungssumme vom Stoßpunkt kleiner ist als im gleichen Zeitintervall vor dem Stoß.

Weitere noch genauer zu untersuchende Vermutungen sind:
- Der Normalraum ist ein dünnes Medium von Uratomen.
- Das Geschwindigkeits-Betrags-Summen-Maximum ergibt sich bei ausgeglichenen Absolutgeschwindigkeiten vieler Stoßpartner.
- Das Geschwindigkeits-Betrags-Summen-Minimum ergibt sich bei unterschiedlichsten Absolutgeschwindigkeiten vieler Stoßpartner.
- Bei Frontalstößen ergibt sich ein Absolutgeschwindigkeits-Betrags- und Anzahldichte-Ausgleich.
- Bei Querstößen ergibt sich oft eine Absolutgeschwindigkeits-Betrags- und
Anzahldichte-Unterschieds-Zunahme.
Vor allem im Hinblick auf mögliche Systembildungen im einfachen HKG muss demnach die Einwirkung von Stößen unter Berücksichtigung des Zeitfaktors untersucht werden.

4. Winkelabhängige Eigenschaftsänderungen im HKG

Eigenschaften im HKG werden natürlich durch die Anwesenheit von Kugeln in bestimmten Raumzeit-Gebieten erzeugt. Am anschaulichsten wäre es nun, durch die Kenntnis sehr vieler Geschwindigkeiten der Kugelmittelpunkte an den Raumzeitpunkten die zeitliche Entwicklung mit den elementaren Wechselwirkungen, also Stößen, einfach über ein bestimmtes Zeitintervall zu verfolgen. Diese rein deterministische Untersuchung hängt für immer von den zufällig oder was eigentlich das Gleiche ist, von den willkürlich gewählten Anfangsbedingungen ab. Wie groß aber das betrachtete Gebiet und die Anzahl der sich darin bewegenden Kugeln auch gewählt wird, schnell kommt es zum Verlassen des Gebietes durch irgendwelche Kugeln. Neue, von außerhalb eindringende müssen deshalb hinzugenommen werden und wiederum stellt sich die Frage nach deren Ort sowie Geschwindigkeit. Diese müssen also ab einer maximal (vom Computersystem abhängigen) betrachtbaren Teilchenzahl durch einen Zufallmechanismus ermittelt werden. Dieser natürliche Zwang für eine Zufallsbetrachtung basiert allerdings trotz allem auf einer deterministischen Welt.

Für die Erzeugung zufälliger Teilchenorte wird anfangs von einer homogenen Gleichverteilung im betrachteten Raum ausgegangen. Daraus folgt, dass auch parallele Flugbahnen, wie bereits vorn bei den Definitionen angenommen, gleichwahrscheinlich sind. Der Mechanismus zur Stoßachsenwinkelerzeugung bleibt demnach wie vorn. Gezeigt wurde vorn auch, dass es beim Kollisionswinkel F durchaus eine Asymmetrie in der Form bevorzugter frontaler Stöße gibt. An diese können eindeutig Flugwinkel b für die stattfindenden Stöße, bei bekanntem Geschwindigkeitsbetrag u eines Probeteilchens, gekoppelt werden. Die Flugwinkel b des HKG seien aber vorerst weiterhin gleichmäßig in allen Raumrichtungen verteilt, weil die Teilchen im Laborsystem eines nach außen offenen Gebietes betrachtet werden.

Ziel der folgenden Untersuchung soll nun erst einmal die Bestimmung der zugrunde zu legenden Geschwindigkeitsverteilung unter dem Einfluss vieler Stöße sein. Die Maxwellsche Geschwindigkeitsverteilung ist dabei nur eines der möglichen Resultate.

Von vorn werden die in einer Datei gespeicherten Geschwindigkeitsvektoren für die weiteren Betrachtungen verwendet. Damit ergeben sich die Geschwindigkeitsbeträge:

(94)

Die normierten Längen u seien deshalb:

(95)

Das erste Teilchen habe bei der ersten Berechnung die oben (92) ermittelte Durchschnittsgeschwindigkeit 1, also

(96)

und alle u haben die oben ermittelte Länge.

Der Stoßpartner v liege nun wie oben aus (68) folgend in der gleichen Ebene, so dass nur ein zufälliger Flugwinkel b für die zu ermittelnden Stöße erzeugt werden muss:

(97)

Die v_i sind mit dem Zufallsgenerator für die N(a,s)-Verteilung zu bestimmen und für die b_i wird der oben entwickelte Zufallsgenerator abgewandelt:

(98)

Mit dem vorn konstruierten Zufallsgenerator (48) können nun von den Geschwindigkeitsbeträgen u_i und v_i abhängige Flugwinkel für Zusammenstöße erzeugt werden

(99)

Die hier anfangs willkürlich gewählte Standardabweichung von 0.3 bedeutet nur dann eine Einschränkung, wenn die nach vielen Stößen sich ergebende außerhalb der numerischen Möglichkeiten von Mathcad liegt bzw. wenn ein prinzipieller Fehler vorliegt.

(100)

Die Geschwindigkeitsbeträge müssen allerdings wegen der Erzeugung mit dem Zufallsgenerator nicht im Durchschnitt exakt 1 ergeben:

Für zu simulierende Stöße werden die bereits in den Definitionen angegebenen Zufallsgeneratoren (1) und (2) verwendet:

Mit den bekannten Transformationen (57), also

lassen sich nun die gewünschten Stöße in der Ebene simulieren. Die Stoßpartner ligen dabei nur vor dem Stoß in einer Ebene. Beim Stoß treten Stoßachsenwinkel außerhalb der Ebene auf, so dass die Vektoren nach dem Stoß in den dreidimensionalen Raum gestreut werden. Das bedeutet aber keine Einschränkung der gewünschten Betrachtung, weil im Prinzip jeder einzelne Stoß für sich betrachtet wird und bei diesem zur Erzeugung des zufälligen b eines aus der Umgebung kommenden Stoßpartners eine Ebene gewählt werden kann. Zur Weiterverwendung als HKG eignen sich die erzeugten Geschwindigkeitsvektoren allerdings nicht. Nur die charakteristischen Eigenschaften der interessierenden Geschwindigkeitsverteilung können ermittelt werden.

(101)

(102)