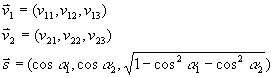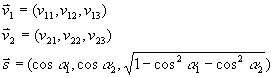Zur vollständigen Beschreibung eines Stoßgebildes
sind insgesamt 10 Parameter erforderlich. Je nach
Anforderung können dies weniger werden. Jeweils
3 Zahlen stehen für die Geschwindigkeitsvektoren vor
dem Stoß, 2 für die Winkel der
Stoßachse, welche hier zufällig in x-Richtung liegt. Diese 8
Zahlen
charakterisieren den Dirac-Spinor. Darüber hinaus
sind 2 Parameter für die Anzahldichte, welche sich
durch das Verhältnis d / L ausdrückt, sinnvoll.
Das ganze Stoßgebilde wird natürlich in der Raumzeit
betrachtet, wodurch noch 4 Zahlen
(Zeit auch imaginär) für die Felddarstellung hinzukommen, die
zwar
nicht das eigentliche Stoßgebilde beschreiben,
aber eine lokale Verzerrung der Raumzeit verursachen.
Die
optimale Beschreibung ist sicher problemabhängig.
Wegen der unmöglichen Feinauflösung bis zu
einzelnen Uratomen müssen in der Raumzeit wahrscheinlichkeitstechnische
Zusammenfassungen
erfolgen.
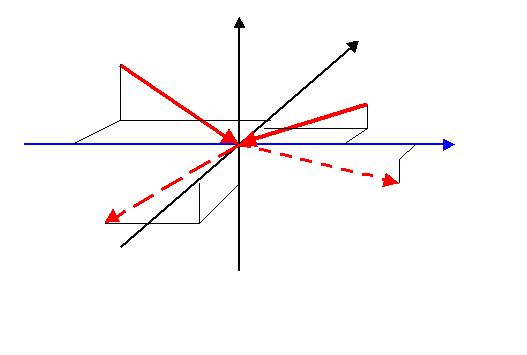 |
Bei Stößen werden nur die Geschwindigkeiten
parallel zur Stoßachse (blau) ausgetauscht.
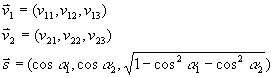
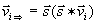
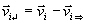
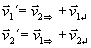
Das ist die Stoßformel des Uratom-Modells.==>
Stoßwahrscheinlichkeitsveränderung
= lokale Raumzeit-Verzerrung |
Jede Geschwindigkeitsänderung ist in gegenseitiger Abhängigkeit
mit einer Anzahldichteänderung verbunden. Deshalb ändert sich
bei jedem Stoß, welcher neben der Mischung (Superposition) von Uratom-Mengen
die einzige Wechselwirkung darstellt, lokal die Auftreffwahrscheinlichkeit.
In einem Raumzeit-Intervall ist diese (Raumzeit-Verzerrung) vom Produkt
aus Anzahldichte mal Geschwindigkeit abhängig.
Durch die elementaren Ereignisse (Stöße) werden
auf natürliche Art Maße für deren Abstand definiert. Für
diese werden kontinuierliche Parametermengen verwendet, welche gemäß
dem üblichen Sprachgebrauch die Namen Länge und Zeit erhalten.
Nur aus der Erfahrung folgt, daß es drei orthogonal
(rechtwinklig) aufeinander stehende Längenmaße und damit Raumdimensionen
gibt. Die Zeit könnte auch den natürlichen Zahlen
zugeordnet werden, weil die Ereignisse im Prinzip abzählbar
sind. Durch die Unkenntnis wird aber alles für die Berechnung zufällig
und ein kontinuierlicher Zeitparameter erforderlich. Nur
in großen Raumzeit-Bereichen entsteht "Schein-Sicherheit". Welche
Zahlenmenge zur optimalen Beschreibung eines Problems zu verwenden ist,
hängt von diesem selbst ab.
Trägheit ist die Eigenschaft der unbeeinflußten
Weiterbewegung von Massen (= Uratom-Anzahl) solange keine
Zusammenstöße erfolgen. Wie sich im Modell noch zeigen wird,
erfolgen im sehr dünnen Uratom-Medium (Vakuum) mit hoher
Wahrscheinlichkeit frontale Zusammenstöße. Diese ergeben
eine solche Symmetrie (gleiche Geschwindigkeit), daß Systembewegungen
durch sie nicht beeinflußt werden. Die Änderung von Systembewegungen
ist dagegen immer durch Änderungen der Stoßwahrscheinlichkeiten
verursacht.
Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell,
http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)