Die hypothetisch kleinsten Objekte sind Demokrits Atome, aus Elementarteilchen zusammen gesetzte Materiebausteine  sollten deshalb besser Struktronen heißen. Stichworte Standardphysik Die diskrete Standardphysik vereinigt die Standardmodelle von Elementarteilchen und Kosmologie durch Einführung einfacher sehr kleiner diskreter Objekte mit einfacher Wechselwirkung durch Geschwindigkeitstausch beim Stoß alte Ideen Stoßtransformationen

Computersimulationen erlauben Untersuchungen, ob in einem einfachen Gas diskreter Objekte (harter Kugeln) Strukturen möglich sind. Diese könnten das Standardmodell erweitern. Uratom-Modell Diskrete Objekte Modell. .pdf Zum Finden werden allgemein Suchmaschinen verwendet, Koordinaten ermöglichen die Lokalisierung. Hier sollen einige Angebote vorgestellt werden (Touristik). z.B. Schiffsreisen Venedig - Istrien.. Technik Privat

Erzeugung der Feinstrukturkonstante durch Simulation von Stößen

Im Rahmen der Idee zu einer diskreten Erweiterung der Standardphysik kam es zur Untersuchung, was in einem einfachen Medium diskreter Objekte passieren kann. In Textform steht das aktuelle Mathcad-Arbeitsblatt als Feinstrukturkonstante.pdf zur Verfügung. Das Original Mathcad-Arbeitsblatt gibt es zusätzlich in verschiedenen Versionen (auch für alte Mathcad-Versionen):

- Feinstrukturkonstante11.mcd

- Feinstrukturkonstante12.mcd

- Feinstrukturkonstante12.xmcd

- Feinstrukturkonstante13.xmcd

- Feinstrukturkonstante14.xmcd auf welches sich die Erklärungen beziehen

- Feinstrukturkonstante14-1360px.xmcd

- Feinstrukturkonstante14ohne Text.xmcd

- Feinstrukturkonstante14_mit-script.xmcd 

- Feinstrukturkonstante.xmcd  Version 08/2013 für Diskussion auf ALLTOPIC,... und Feinstrukturkonstante-xmcd.pdf dazu

- 2013-Feinstrukturkonstante.mcdx erste Version für MCAD-Prime 2.0 und  2013-FeinstrukturkonstanteV3.pdf dazu

-  Die Testversion, welche erneutes Eintippen ersparte, wurde freundlicherweise vom Benutzer kurzpa ins neueste Mathcad-Format umgewandelt wurde (.pdf dazu). Auf Mathcad-Express funktioniert allerdings die Funktion xyz2sph nicht (weil sie nur der Premium-Version vorbehalten ist). Eine Lösung dafür wird noch gesucht, weil Mathcad-Express auch keine Programmierung erlaubt. Ende 2013 gelang nun endlich die Erzeugung eines auf  Mathcad  Prime 2.0 lauffähigen Feinstrukturkonstante.mcdx, mit welchem jetzt 1 Million Stöße in einem Durchlauf simuliert werden können.

- 2020 FSK-Iteration zur Ergänzung von 2015-Feinstrukturkonstante.pdf zeigt, dass Vereinfachungen der Iteration zu gleichen Resultaten führen. Im einfachsten Fall bleibt ein Zahlenfaktor, hinter dem sich eine erzeugende Struktur verbergen sollte.

Die älteren Versionen, bis auf die mit dem Text für das AutoHotkey Script sind gleich und nur in Mathcad 14 unterschiedlich abgespeichert. Empfehlenswert ist das Herunterladen der kostenlosen (30-Tage) Mathcad 15-Version bzw. von Mathcad Prime 2.0 oder jetzt schon 3.0 von:

http://www.ptc.com/products/mathcad/mathcad-15-0/free-trial.htm  oder auch http://www.comsol.net/index.php/de/mathcad-download

Im neuesten Test soll vor allem nachvollziehbar gezeigt werden, dass keine mit der Feinstrukturkonstante irgendwie zusammenhängende Zahlen in die Simulation gesteckt werden. Das kann  im Forum:

ALLTOPIC unter dem Thema: "Erzeugung der Feinstrukturkonstante durch Stöße" verfolgt werden. Versucht wird zusätzlich das kostenlose Computer Algebra System SMath Studio, für das es auch ein deutschsprachiges kostenloses Handbuch gibt.

Das begleitende Test-FSK.sm ist ein Arbeitsblatt (als .pdf), welches dem von Mathcad entspricht und vorerst bis zu den Stoßtransformationen diskutiert wird, weil diese Schlüssel für eine diskrete Erweiterung der Standardphysik und damit auch der Erzeugung von Naturkonstanten im betrachteten Substrat sind.

Unter anderem wurden viele elementare Wechselwirkungen (Stöße) untersucht. Dabei wurde festgestellt, dass als kumulativer Wert von Geschwindigkeitsbetragsänderungen der Zahlenwert langsam gegen den der Feinstrukturkonstante konvergiert. Im letzten .pdf sind über 300 Millionen Stöße berücksichtigt. Das untersuchte Substrat (des Vakuums) wird durch folgende Voraussetzungen definiert:

Es existiert einzig und allein eine Menge unendlich vieler, sich im dreidimensionalen Raum bewegender diskreter Objekte, die hier als gleich große (harte) Kugeln angenommen werden. Diese durchdringen den leeren Raum gleichförmig geradlinig. Eine Annäherung an eine andere Kugel erfolgt bis zum Zusammenstoß (Berührung), bei dem nur die Geschwindigkeits­komponenten in Richtung der Stoßachse (Berührungsnormale) ausgetauscht werden.

Damit ergibt sich als einfacher Ansatz für Rechnungen ohne Berücksichtigung der Raumzeit folgende lokale skalierbare Situation:

Es wird eine Menge V unendlich vieler Geschwindigkeitsvektoren im R³ mit isotroper Orientierung untersucht. Deren Maxwell-Boltzmannsche-Geschwindigkeitsverteilung(en) mit dem Parameter a wird durch die zu definierende elementare Wechselwirkung aus beliebigen Anfangsgeschwindigkeiten erzeugt.

Die laut Voraussetzung vorhandene Ausdehnung führt unter der Vorstellung gleich wahrscheinlicher paralleler Flugbahnen zum Auftreten von Berührpunkten, welche mit den zwei Winkeln φ und θ beschrieben werden. Damit ergeben sich folgende Transformationen einer elementaren Wechselwirkung (als Stoß vorstellbar):

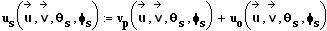
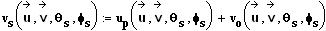
wobei in der Klammer die acht reellen Parameter der Geschwindigkeitsvektoren vor dem Stoß und die Stoßachsenwinkel stehen Das sind im Mathcad-Arbeitsblatt die Stoßtransformationen (12) und (13), welche die elementaren Wechselwirkungen in dem angenommenen Substrat beschreiben. Die detaillierte 3-dimensionale Darstellung und Diskussion erfolgt mit dem herunterladbaren Test-FSK.sm.

Die Auswahl von N zu simulierenden Stoßpartnern erfolgt durch Bestimmung von zufälligen Geschwindigkeitsbeträgen nach der Inversionsmethode aus den vorliegenden (auch etwas unterschiedlichen) MB-Verteilungen. Trotz Isotropie werden zu einem bereits ausgewählten u, dessen Bewegung in z-Richtung gelegt werden kann, relativ zu diesem Bahnenwinkel (Vektorwinkel) so ausgewählt, dass deren Häufigkeit von der richtungsabhängigen Stoßfrequenz, auf dieses bewegte Objekt zu, bestimmt werden. Häufiger sind Stöße aus den Richtungen, wo die Relativgeschwindigkeit groß ist.
Nach N Stößen konvergiert der Durchschnitt der Betragsänderungen

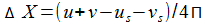für N->oo gegen α ~ 1/137.036 (0.00729735252051).

Darüber hinaus wäre eine Untersuchung von Ortsänderungen und der sich daraus ergebenden Stoßwahrscheinlichkeiten erforderlich. Dieser riesigen Aufgabe wird durch Ausnutzen angenommener Symmetrien in dem betrachteten Substrat ausgewichen.

Bei den eigentlichen Simulationen wird mit der Definition der in einem Durchlauf zu betrachtenden diskreten Objekte begonnen. Diese Zahl N sollte für einen Probelauf klein genug sein (z.B. 10.000), damit schnell ein Ergebnis erscheint. In (18) sollte durch Rechtsklick die Berechnung des Kumulativwertes erst einmal ausgeschaltet sein, weil wir ja keine der Feinstrukturkonstante bereits nahe Zahl schon am Anfang in die Berechnung hinein stecken wollen. Am besten (und ehrlichsten) ist der Beginn mit a = 0. Allerdings gibt es auch eine gewisse Berechtigung, in einer späteren Phase hierbei etwas Nachzuhelfen, um die Zahl der nötigen Durchläufe für eine Bestimmung weiter hinten liegender Kommastellen abzukürzen. Wichtig  ist bei Neustarts von Mathcad, dass jedes Mal unter Tools in den Arbeitsblatt-Optionen der Anfangswert für die Zufallszahlenerzeugung geändert wird. Sonst werden die Werte mit den Pseudo-Zufallszahlen vorhergehender Durchläufe einfach wiederholt.

Am Anfang, also beim ersten Durchlauf, sollte in (47) erst einmal das APPEND durch WRITE ersetzt werden, um einen ersten Wert in die wichtige Datei DeltaV.prn zu schreiben.

Bei der Auswertung, welche nach jedem Durchlauf erfolgt, sollte im Bild 4 erst einmal die maximal angezeigte Zahl k auf einen kleinen Wert gesetzt werden (Anklicken des Bildes). Nach dem ersten Durchlauf sollten Δ und alpha_d-1 übereinstimmen. Meistens wird eine Zahl in der Größenordnung von 0.00728... heraus kommen, seltener ein Wert größer als 0.00729 und mit etwas Glück sogar schon ein Wert nahe der Feinstrukturkonstante. Wichtig ist aber, dass kein Parameter in das System gesteckt wird, welcher die Zahl nahe der Feinstrukturkonstante hervorrufen könnte.

Für die weiteren Durchläufe hat sich ergeben, dass eine Korrektur der zugrunde gelegten Maxwell-Boltzmannschen Geschwindigkeitsverteilung eines Stoßpartners empfehlenswert ist. Ein halber Inhalt der durch vorhergehende Stöße mit deren durchschnittlichen freien Weglängen aufgespannten Kugel zeigte sich als sinnvoll. Wegen der Skalierungsmöglichkeit brauchen aber weder Objektdurchmesser noch freie Weglängen hier berücksichtigt zu werden. Mit der Wahrscheinlichkeitsdichte ergeben sich für die Geschwindigkeitsbeträge u und v nun die Zufallsgeneratoren, welche N zufällige Maxwell-Boltzmann verteilte Geschwindigkeitsbeträge liefern. Zur Verringerung der Rechenschritte sollen möglichst Zahlen aus jedem Intervall vorkommen. Die Wirkung dieses Mechanismus kann man sich am besten dadurch vergegenwärtigen, dass man rechts unterhalb im Arbeitsblatt u_i = und v_i = einträgt, so dass dort die errechneten Zahlenwerte angezeigt werden. Diese Methode empfiehlt sich übrigens immer, wenn etwas nicht klar ist.

Um eine Zahl mit sehr vielen exakten Nachkommastellen heraus zu bekommen und vielleicht die CODATA-Angaben noch zu übertreffen, ist vermutlich noch höhere Rechengenauigkeit als mit Mathcad erforderlich. Noch nicht berücksichtigt und vielleicht mit einem Einfluss auf hintere Kommastellen ist eine mögliche Veränderung von Verteilungsfunktionen für die Winkel. Das könnte mit den Drehungen der Relativgeschwindigkeiten (in der hier nicht nötigen Sprache der Relativitätstheorie wären das eigentlich Differenzgeschwindigkeiten) bei jedem Stoß zusammen hängen. Tritt dann das erwartete Ergebnis ein, ist das ein untrüglicher Hinweis auf die tatsächliche Existenz eines diskreten Substrats, welches überall vorhanden ist, wo die Feinstrukturkonstante eine Rolle spielt, also auch überall, wo Elementarladungen auftreten und die elektromagnetische Wechselwirkung zur Erklärung verwendet wird. Die Quantenelektrodynamik sollte deshalb mit diesem Substrat (durch Axiom definiert) herleitbar sein.

Aktuell ist mit Mathcad die Feinstrukturkonstante auf sieben Nachkommastellen genau bestimmt, weitere Kommastellen erfordern viel höhere Rechenzeit.   

Die Originaldaten und kumulativen Werte der fortlaufenden Simulationen (pro Durchlauf 100.000 Stöße, ab 2060. Durchlauf jeweils 250.000 Stöße, in Mathcad Prime bis zu 10 Millionen) können als .txt Datei herunter geladen werden. Für einen Einsatz in einer Simulation mit Mathcad muss nur das identische DeltaV.prn ins gleiche Verzeichnis wie Mathcad kopiert werden.

Wesentliche Erkenntnis im aktuellen Entwicklungsstand ist, dass alle Rechnungen auch in anderen  Computer Algebra Systemen und Programmiersprachen reproduziert werden können. In C ergaben sich so die gleichen Zahlenwerte für die Simulation (bzw. Monte-Carlo-Integration) ohne die Rückkopplung. Die dafür eingesetzten Faktoren 1 / (4 pi) in (62) und (3 /( 2 pi)) in Gleichung (64) sind der jetzt vollkommen vom übrigen Teil getrennte Rest, den man als Numerologie interpretieren kann. Dafür muss noch eine physikalische Begründung gefunden werden.

Stichworte (Ende)

Wiese, Albert Lothar: Diskrete Erweiterung der Standardphysik, http://struktron.de, Porec/ Sarajevo 2000-2020
Uratom (Anfang)