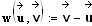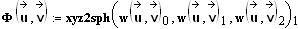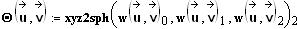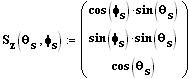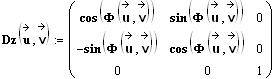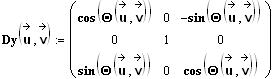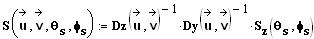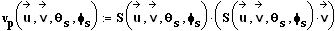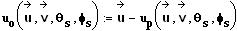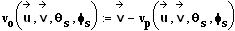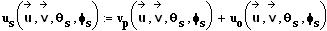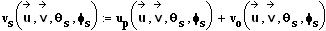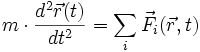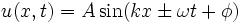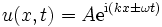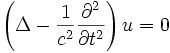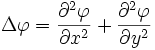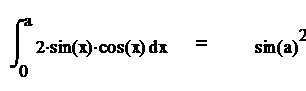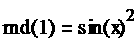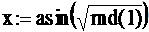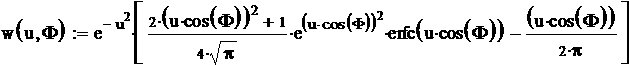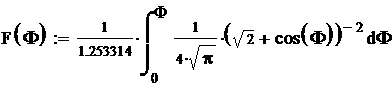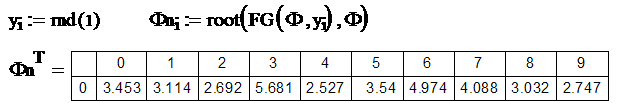| Physik-FAQ | Links zur Physik | Diskussionen | Beweisideen zum DOM |Thermalisierung |

2.2 Elementare Bewegungsgleichungen ohne Potenzial

Einzige Änderung gegenüber der Standardphysik ist in diesem Modell die Einführung der elementaren Wechselwirkung beim Stoß durch einfachen Geschwindigkeitsübertrag auf den Stoßpartner in Richtung der Berührungsnormale. Zur mathematischen Beschreibung ergeben sich folgende, hier ausführlich hergeleitete Bewegungsgleichungen für das ortslose HKG.

 Stoßtransformationen

Für die Untersuchung einer größeren Menge Stöße in einem Gas harter Kugeln eignet sich die Einführung einer sehr einfachen und vor allem leicht zu begründenden Wechselwirkung. Bei der Berührung zweier harter Kugeln kann die Geschwindigkeit wegen des Widerstandes der anderen Kugel in Richtung der Berührpunktnormale nicht weiter mit der ursprünglichen Kugel fortgesetzt werden. Das geht nur auf der anderen Kugel. So überträgt sich der Geschwindigkeitsbetrag parallel zu dieser vollständig auf die jeweils andere Kugel. Orthogonale Geschwindigkeitskomponenten werden dagegen nicht in ihrer freien Bewegung durch den leeren Raum gehindert und setzen sich auf den ursprünglichen Kugeln fort. Die stoßenden Vektoren 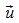und 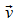haben jeweils 3 Komponenten.

Für die Stoßachsenermittlung ist zuerst die Relativgeschwindigkeit erforderlich:

(1)

Die Richtung der Relativgeschwindigkeit wird mit der Kugelkoordinaten-Transformation ermittelt, für welche hier die in Mathcad eingebaute Funktion verwendet wird:

(2)

(3)

Diese Funktionen entsprechen den ausführlichen Transformationen gemäß dem Artikel über Kugelkoordinaten in Wikipedia. Dabei nimmt Ф Werte von 0 bis 2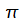 an und Ө Werte von 0 bis .

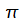Die Stoßachsenwinkel ergeben sich vorerst hier zufallsabhängig, könnten aber durchaus auch von der näheren Umgebung abhängen. Der Winkel 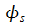kann Werte bis 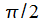annehmen und 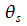Werte von 0 bis 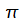, wobei gleich wahrscheinliche parallele Bahnen zur Richtung der Relativgeschwindigkeit angenommen werden. Das ist auf gleich wahrscheinliche parallele Bahnen bei den Stoßpartnern zurückzuführen (siehe unten). Damit ergibt sich in kartesischen Koordinaten der Stoßachsenvektor:

(4)

Dieser wurde relativ zur Richtung der Relativgeschwindigkeit 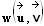erzeugt und muss nun im ursprünglichen Koordinatensystem (dem Laborsystem von 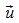und 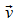) ausgedrückt werden, was durch zwei hintereinander ausgeführte Drehungen erreicht wird:

(5)

(6)

Damit ergibt sich die Stoßachse im ursprünglichen Koordinatensystem durch das zweifache Zurückdrehen zu:

(7)

Dieses S entspricht beim Zentralstoß auf eine ruhende Kugel dem ursprünglichen 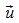bzw. beim Zentralstoß auf ein beliebiges 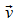allgemeiner dem Relativgeschwindigkeitsvektor 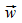normiert auf 1. Beim Stoß werden nun die zur Stoßachse parallelen Geschwindigkeiten der beiden beteiligten Kugeln ausgetauscht. Alle Vektoren sollen jedoch weiterhin im ursprünglichen Koordinatensystem betrachtet werden. Die parallelen Komponenten sind:

(8)

(9)

und die dazu orthogonalen Geschwindigkeitskomponenten:

(10)

(11)

und somit ergeben sich die Geschwindigkeiten nach dem Stoß:

(12)

(13)

(12) und (13) sind die Stoßtransformationen für dreidimensionale Geschwindigkeitsvektoren. Es sind jeweils Funktionen von acht Parametern, also je drei Geschwindigkeitskomponenten in kartesischen Koordinaten und zwei Winkeln für die sich zufällig ergebende Stoßachse. Diese hier ausführlich abgeleiteten Funktionen hängen jeweils von vorherigen (weiter oben) definierten ab, die alle ineinander eingesetzte dreidimensionale Geschwindigkeitsvektoren sind. Trajektorien (Bahngleichungen), also die Lösungen der Bewegungsgleichungen der bewegten Objekte, ergeben sich daraus durch Multiplikation mit der Zeit. Will man nur die Veränderung eines dreidimensionalen Vektors betrachten, kann man die Transformation als Multiplikation einer Matrix mit dem Vektor und anschließende Addition eines zweiten Vektors schreiben. Aus jedem dreidimensionalen Vektor kann jeder andere durch einen geeigneten Stoß erzeugt werden. Die Stoßachse, welche durch zwei Winkel beschrieben wird, ist hier in x-Richtung gedreht.

In die Stoßtransformationen gehen acht Parameter (zwei mal drei für die Geschwindigkeiten und zwei für die Stoßachsenwinkel) ein, welche in Abbildung 3 als Stoßgebilde veranschaulicht sind. Dabei wird nicht die normale Darstellung von Vektoren verwendet, sondern Pfeile, welche gleichzeitig auch den Anfangs- und Endort in einem sinnvoll gewählten Zeitintervall darstellen. Über die mathematischen Eigenschaften eines Gebildes aus den acht reellen Parametern kann und soll hier nicht spekuliert werden.

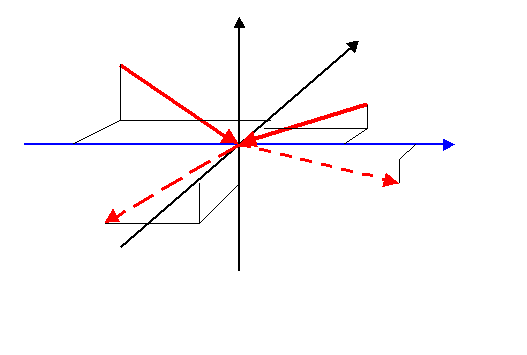
Abbildung 3: Stoßgebilde

Interessant ist hier aber trotzdem, dass möglicherweise erstmals darauf hingewiesen wird, dass eine affine Transformation eines Geschwindigkeitsvektors direkt durch einen anschaulichen physikalischen Vorgang, also ein zweites mit dem ersten zusammenstoßendes Objekt, erzeugt werden kann. Das könnte Ausgangspunkt für vielfältige Theorien werden, vor allem wenn man zusätzlich an die Möglichkeiten von Mittelfeld-Theorien denkt.

Differenzierbarkeit

Durch einfaches Einsetzen von Werten in die Stoßtransformationen erkennt man, dass die Geschwindigkeiten sich bei einem Stoß im allgemeinen abrupt in Richtung und Betrag ändern. Der Graph hat also einen Knick. In diesem Punkt ist die Geschwindigkeitsfunktion demnach auch nicht ableitbar. Schon hier kommen wir zu einem Widerspruch zur bewährten Beschreibung von Bewegungsabläufen durch differenzierbare Funktionen nach Newton. Daraus folgt gleich die Sorge, die neu eingeführten spontanen Bewegungsänderungen wieder verwerfen zu müssen, um den bewährten Newtonschen Apparat zu erhalten. Paradox erscheint vor allem, dass mit den Stoßtransformationen schwerer die kleinen infinitesimalen vielfach beobachtbaren Geschwindigkeitsänderungen erklärbar sind, als abrupt große Geschwindigkeitsbetragssprünge.

Bei tatsächlich beobachteten Phänomenen, wie dem einfachen Stoß zweier gleich großer und gleich schwerer Billardkugeln ergibt sich bereits das Problem der korrekten mathematischen Beschreibung. Ein Weg ist die Verwendung eines unendlich starken Potenzials, oder z.B. eines sehr starken Lennard-Jones-Potenzials V(r) = a r^-12 - b r^-6 . Im ersten Fall kommt das Ergebnis korrekt heraus, die Geschwindigkeitsfunktion ist aber am Wechselwirkungspunkt nicht differenzierbar. Im zweiten Fall ist die Funktion differenzierbar und der Fehler gering, die Kugeln können aber nicht als Punkte betrachtet werden, weil sonst trotzdem das Potenzial über alle Grenzen wachsen würde.

Eine Aufgabe der Forderung nach Differenzierbarkeit im ganz Kleinen erfordert zu deren Ersatz bei allen beobachtbaren Phänomenen die Anwendung verschiedener Tricks, wie z.B. einer Mittelwertbildung, wie sie so oft um uns herum erfolgt. Wichtige Beispiele wurden schon in 1.2 erwähnt. Hier betrachten wir wegen der bildlichen Vorstellbarkeit einfach die Darstellung eines Gradientenfeldes. Die Ableitung in jedem Punkt wird durch einen kleinen Pfeil dargestellt. Diesem entspricht im zu entwickelnden Modell die Bewegung von immer noch vielen sehr kleinen Objekten. Jeder einzelne Pfeil kann durch die Mittelwertbildung aus vielen Objektbewegungen und den dabei stattfindenden Stößen entstehen. Selbst der scheinbar so kontinuierliche Graph einer Kreisbewegung auf einem Computerbildschirm wird bei genauer Betrachtung mit einer Lupe etwas Diskontinuierliches. Wir haben uns aber daran gewöhnt und nehmen die für unser Auge nicht wahrnehmbaren Fehler in Kauf.

Für die Beschreibung aller Naturphänomene können deshalb beliebig oft differenzierbare Funktionen wie gewohnt verwendet werden. Im ganz Kleinen muss nach diesem Modell hinter jeder überall differenzierbaren Funktion etwas noch Kleineres verborgen sein. Zugehörige Theorien für alles Größere sind demnach effektive Theorien. Erst an der Grenze der unteilbaren Objekte, die Demokrit Atome nannte, geht die Differenzierbarkeit verloren. Es handelt sich dabei aber hier nicht um die heute als Atome bezeichneten Objekte, weil diese ja sehr wohl weiter teilbar sind. Wie schon erwähnt, beschäftigen sich unter anderem auch die „Mean field theory“ (Mittelfeldtheorie, im deutschen Sprachraum Molekularfeldtheorie) und etwas auch die Stochastische Dynamik mit einem möglichen Zugang zur Quantenphysik über Mittelwerte.

Bewegungsgleichungen

Grundlage für den Formalismus aller Feldtheorien zur Beschreibung der Dynamik kleiner quantenmechanischer Systeme (Elementarteilchen) sind die Lagrangedichten. Die historische Rückwärts-Verfolgung der Entwicklung dieses Formalismus führt beispielsweise über den Lagrange-Formalismus, die Lagrangefunktion, zum D'Alembertschen Prinzip, in das die Differenzen aus kinetischer und potenzieller Energie so eingehen, dass bei der Variation die Summe der verrichteten Arbeit verschwindet. Die einzelnen Differenzen aus Teilchenbeschleunigung und auf das betrachtete Teilchen wirkender Kraft brauchen nicht zu verschwinden. Unbeantwortet blieb aber schon in der klassischen Mechanik die Ursache der einzelnen Teilchenbeschleunigungen.

Etwas moderner und mit einem Computer Algebra System nachvollziehbar (z.B. M. Komma, Moderne Physik mit Maple, 4.1.2) ist eine ähnliche Überlegung mit virtuellen Bahnen stückweise gleichförmiger Bewegungen, welche zur Feynmanschen Pfadintegralmethode führt. Aber auch die Propagatoren der Quantenfeldtheorien benötigen im Endeffekt Erklärungen der in sie eingehenden elementaren Bewegungsgleichungen der Form:

(14)

In diesen Gleichungen werden zur Beschreibung von Bewegungsänderungen, zweite Ableitungen benötigt. Auch alle Potenziale, welche ja die Beschleunigungen hervorrufen, verwenden dazu zweite Ableitungen von Ortsfunktionen nach der Zeit. Erklären können diese aber die dahinter stehenden Vorgänge im ganz Kleinen nicht. Im Gegenteil gibt es sogar Probleme bei der Vorstellung des Anwachsens von Kräften über alle Grenzen, wenn man sehr kleine Abstände betrachtet, wie sie bei der Beschreibung mit punktförmigen Teilchen vorkommen.

Im hier zu entwickelnden Modell können nun an den Stellen von Wechselwirkungen, also Orten wo sich zu bestimmten Zeiten Geschwindigkeiten von Objekten ändern, überhaupt keine Ableitungen angegeben werden. Die Trajektorien weisen dort Knicke auf und die Lage der Tangenten wird unbestimmt. Wie sollen nun aber die Gleichungen (12) und (13) die üblichen Bewegungsgleichungen, wie (14) ersetzen? Die Antwort ist eigentlich schon in den vielen Theorien, welche mit Durchschnitten arbeiten, also effektiven Theorien, vorhanden. Es geht demnach nur um die Akzeptanz instantaner Geschwindigkeitsänderungen und der Existenz von etwas Kleinerem als den Elementarteilchen des Standardmodells. Daraus folgt dann, dass jedes Objekt, das sich auf einer gekrümmten Trajektorie bewegt, aus kleineren Objekten bestehen muss, deren Schwerpunktbewegung gerade durch die Bahn beschrieben wird. Unerheblich ist dabei, welches der beiden am Knick zusammenstoßenden Objekte nach dem Stoß als zum System gehörend betrachtet wird. Die Ungenauigkeit dieser Bahn von Elementarteilchen, deren Beschreibung durch die Unschärferelation bestimmt wird, braucht dann nur eine entsprechende Interpretation als etwas wirklich Existentes. Formale Hilfsmittel dazu liefert die Ensemble-Interpretation. Allerdings wird der Ensemble-Begriff bereits auf die kleinsten im Standardmodell betrachteten Objekte, also Elementarteilchen, angewendet und weil diese sich ja bekanntlich auf krummen Bahnen bewegen können, wie beispielsweise Elektronen in einem Magnetfeld, muss dieser Ensemble-Begriff auf die kleineren Objekte des HKM´s verallgemeinert werden. Alle zur Beschreibung von Elementarteilchen benötigten Felder sollten deshalb aus den kleineren Objekten konstruiert werden können und bieten somit eine Erklärungsmöglichkeit der Bewegungsgleichungen mit Hilfe kleinerer bisher verborgener Objekte.

Betrachten wir als Beispiel die klassische Wellengleichung:

In einer Dimension wird diese

bzw.

(15)

in komplexer Darstellung und allgemein (vierdimensional)

(16)

Dabei ist c die Ausbreitungsgeschwindigkeit und Δ der Laplaceoperator. Für eine Funktion φ(x,y) von zwei Variablen ergibt sich in kartesischen Koordinaten mit φ(x,y) beispielsweise

(17)

Die Wellengleichung beschreibt demnach, wenn wir sie an einem bestimmten Raumzeit-Punkt betrachten, gerade die gekoppelte Änderung zweier Eigenschaften, welche wie die Bewegungsgleichungen (14) zweite Ableitungen nach der Zeit verwenden. Bei genauer Betrachtung lässt sich feststellen, dass beispielsweise bei der Beschreibung einer Schallwelle sich Druck bzw. Anzahldichte und Schnelle bzw. Geschwindigkeit in gegenseitiger Abhängigkeit ändern, bei elektromagnetischen Wellen dagegen elektrische und magnetische Feldstärken. Für solche Phänomene bietet sich nun als tiefer greifende Erklärung die bei Stößen vorkommende Vergrößerung der Geschwindigkeit des einen und Verkleinerung der Geschwindigkeit des anderen Partners an. Verbunden mit Geschwindigkeitsänderungen sind in der gleichen Richtung wegen des langsameren oder schnelleren Entfernens von dem Stoßpunkt Dichteänderungen. Langsames Entfernen bedeutet Dichtezunahme und schnelles Entfernen Dichteabnahme (Achtung: freie Weglängen sind normalerweise von der Geschwindigkeit unabhängig). Die erwartete Stoßfrequenz bestimmt sich aber aus dem Produkt von Geschwindigkeitsbetrag und Teilchenzahldichte in einer Richtung. Deren Betrachtung soll weiter unten zur Beschreibung elektromagnetischer Felder führen.

Es ist also festzustellen, dass die übliche Beschreibung der Dynamik von klassischen mechanischen Systemen bis zu Objekten der Quantenfeldtheorie grundsätzlich auch mit den Stoßtransformationen erfolgen kann. Dazu müssen allerdings den bewährten Feldern auf der niedrigsten Stufe der Standardphysik über die Wahrscheinlichkeitsinterpretation die harten Kugeln zugeordnet werden. Anfangswerte für die vielen kleinen Objekte sind dann beispielsweise durch Zufallsgeneratoren zu ermitteln.

Wahrscheinlichkeitsfelder

Felder beschreiben Eigenschaften an Punkten der Raumzeit, wobei nicht unbedingt deren Beschreibungsweise aus der Relativitätstheorie verwendet werden soll. Die Metrik der Raumzeit selbst wird auch als Feld aufgefasst. Dieser Gedanke ist beispielsweise zur Herleitung der ART nützlich. Alle möglichen in der Standardphysik verwendeten Feldtheorien beschreiben (meist quantenmechanische) Objekte, für die nur Wahrscheinlichkeiten angegeben werden können, das Objekt in einem Raumzeit Bereich anzutreffen. Allgemein kann jedem Mittelwert ein Maß und deshalb auch eine Wahrscheinlichkeit zugeordnet werden. Als besonderes Beispiel interessieren hier natürlich die Felder, welche den betrachteten Objektbewegungen und daraus abgeleiteten Größen Wahrscheinlichkeiten zuordnen.

Kugelbewegungen spannen im hier zu entwickelnden HKM, unter Annahme von deren Unkenntnis an einem Raumzeitpunkt, gegenüber jedem anderen Objekt einen geometrisch beschreibbaren Raumbereich auf (Abbildung 2). Nur wenn die Relativgeschwindigkeit auf die betrachtete Probekugel zeigt, kann es zu einem Stoß kommen. Alle solchen Bereiche überlagern sich (superponieren). Daraus kann die Stoßfrequenz auf ein Probeteilchen aus den verschiedenen Raumrichtungen ermittelt werden. Eine erwartete Stoßfrequenz ergibt eine Stoßwahrscheinlichkeit. In deren Berechnung müssen Wahrscheinlichkeitsverteilungen von, möglicherweise gerichteter, Teilchenzahldichte und Geschwindigkeiten eingehen. Häufig wird davon ausgegangen, dass deren Wahrscheinlichkeitsverteilungen, vor allem auch im Hinblick auf ihre Komponenten, voneinander unabhängig sind. Damit lässt sich leichter rechnen. Im HKG, wo mögliche Strukturen untersucht werden sollen, sollte aber der Einfluss lokaler Abweichungen der Anzahl- und Geschwindigkeitsverteilungen von dem aus der kinetischen Gastheorie bekannten Standardwert (Maxwell-Boltzmann-Verteilung) nicht vernachlässigt werden. Daraus folgt, dass nach Stößen die Erwartungswerte in der Umgebung korrigiert werden sollten. Übrigens führt das auch zu der Idee, selbst die Teilchenzahldichte nicht mehr nur als Skalar zu betrachten. Viele Teilchen in der Nachbarschaft eines Probeteilchens, die aber in einer Scharbewegung nicht in dessen Richtung fliegen, haben für die Stoßfrequenz, auf das Teilchen zu, einen geringeren Einfluss, als wenn sie sich in dessen Richtung bewegen würden. So ist zu überlegen, die Teilchenzahldichte möglicherweise vektoriell und vielleicht auch komplex (Geschwindigkeit und Dichte gekoppelt) zu beschreiben, um diese Eigenschaften mit zu erfassen. Die Maxwellschen Gleichungen des elektromagnetischen Feldes sind ein Hinweis auf eine solche Beschreibungsmöglichkeit. Elektrische Ladung bzw. Ladungsdichte müssen zu einer solchen Interpretation allerdings mit den bei Stößen erzeugten, vom Durchschnittswert abweichenden, Geschwindigkeitsbeträgen verknüpft werden. Anstelle der Teilchenzahldichte kann beispielsweise zur Beschreibung des gleichen Sachverhalts die freie Weglänge verwendet werden, wodurch eine einfachere Zuordnung der beschreibenden komplexen Zahl zur Stoßfrequenz erreicht wird. Der Realteil könnte dabei dem Geschwindigkeitsbetrag 0<v<oo entsprechen, der als elektrische Feldkomponente interpretiert werden kann und der Imaginärteil dem Kehrwert der freien Weglänge 0<1/L<oo entsprechen, was dann eine Magnetfeldkomponente wäre (das < -Zeichen steht, weil die freien Weglängen immer größer als die Abstände der Mittelpunkte beim Stoß sind). Jede solche komplexe Feldkomponente kann natürlich in beliebigen Raumrichtungen unterschiedliche Werte besitzen und beschreibt auch eine Stoßfrequenz. Dazu sind weitere Parameter erforderlich.

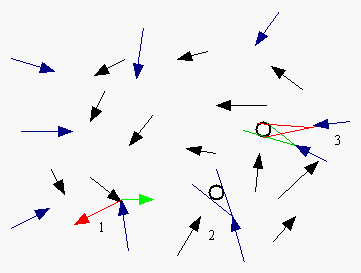
Abbildung 4: Stoßbereichsüberlagerung

In Abbildung 4 ist das Problem angedeutet. Bei 1 ist eine Änderung der Geschwindigkeiten gezeigt, die in die Wahrscheinlichkeit für einen Stoß des zweiten Teilchens eingehen könnte und bei 2 aber nicht berücksichtigt ist. Bei 3 ist eine Stoßkegelüberlagerung eingezeichnet, die im Hinblick auf die generelle Unsicherheit der Orte und Geschwindigkeiten eigentlich noch durch alle anderen Teilchen beeinflusst wird. Hier äußert sich bereits das intuitiv überall vermutete Gesetz, dass genau das geschieht, was die Umgebung erzwingt und nichts anderes.

Das Bild veranschaulicht übrigens auch die Wahrscheinlichkeitsveränderungen bei höheren Stufen der Systembildung, wie Elementarteilchen bis zu Sternen,... Die Berechnungen erfolgen dann beispielsweise mit den Methoden der Eichtheorien. In den höheren Stufen können dafür systeminterne Eigenschaften im Sinne effektiver Theorien z.B. zu Quantenzahlen (diskrete Eigenschaften zur Beschreibung von Stabilität) oder neuen Dimensionen zusammengefasst sein. Deshalb werden kompliziertere geometrische Gebilde erforderlich (Tensoren, Spinoren).

Der Versuch (Wheeler) zur Erweiterung der ART durch die Entwicklung einer Geometrodynamik führte nicht zum gewünschten Erfolg. Die eingeführten Geonen warfen andere Probleme auf und der Weg wurde kaum weiter verfolgt. Besser könnte die gedankliche Loslösung von eigenständigen „Teilchen“ in den höheren und komplizierteren Stufen der Beschreibung sein. Wenn alle Elementarteilchen nur auf die dynamische Struktur der elementaren Objekte zurück zu führen sind, werden deren Eigenschaften durch superponierte Wahrscheinlichkeiten erklärt. In Stoßversuchen benötigen die dort erzeugten oder beobachteten Elementarteilchen teilweise sehr hohe Energie, was möglicherweise ein gewisses dafür notwendiges Stabilitätskriterium darstellt. Als Ansatz zur Beschreibung könnte die Quantengeometrie verwendet werden. Die dynamische Beeinflussung von Stoßwahrscheinlichkeiten bringt aber gewaltige mathematische Probleme mit sich, die in Abbildung 3 nur angedeutet sind und sich auf alle größeren Systeme übertragen. Einen Lichtblick bzw. eine Hoffnung auf das tiefere Verständnis der Ursachen bietet das HKM. Alle wichtigen verwendbaren Felder sollten aus Mengen der betrachteten kleinsten Objekte erzeugbar werden. Dann erst wäre eine zugehörige Theorie fertig. Umgekehrt müssen dann aber auch alle Felder der Standardphysik so interpretiert werden können, dass die kleinsten Objekte als Bestandteile, mit einer nur den geometrisch erklärbaren Zufallsgesetzen unterliegenden Dynamik, daraus generierbar werden. Wegen der Gültigkeit der Zufallsgesetze gilt auch das Gesetz der großen Zahlen. Die zu betrachtenden Systeme werden hauptsächlich durch die bei den Stößen vorkommenden Winkel beeinflusst. Kleine Unterschiede führen bei der Fortbewegung nach Stößen aber bereits nach kurzer Zeit zu großen Ortsunterschieden. Deshalb können in Systemen mit kleiner Anzahl beteiligter Kugeln kaum Asymmetrien erwartet werden, die nicht nach kurzer Zeit durch zufällige Stöße und damit zusammen hängende Fluktuationen zur Auflösung des Systems führen. Erst bei wirklich großer Anzahl der zu dem System gehörenden kleinsten Kugeln kann das Gesetz der großen Zahlen zu einem durchschnittlichen Ausgleich der Störungen führen.

Als Hilfsmittel zur Bestimmung der Parameter für infrage kommende, auch mehrdimensionale Wahrscheinlichkeitsverteilungen können Simulationen, besonders Monte-Carlo-Simulationen oder beispielsweise ein Molekular-Dynamik-Simulator bzw. die Sinai-Billard-Simulation vieler Teilchenstöße dienen. Damit werden die Erwartungswerte und Varianzen zwar deterministisch erzeugt, können aber beispielsweise durch Randbedingungen (Wandstöße) zufällig beeinflusst werden. Die Zahl der untersuchten Stöße ist aber noch zu gering, um Aussagen über mögliche Struktur- bzw. Clusterbildung im HKG zu wagen.

Zufallsgeneratoren

Durch eine bisher weniger beachtete Art der Simulation eines HKG´s kann möglicherweise in Hinsicht auf mögliche Strukturbildungen mehr erreicht werden. Bekannte geometrische Objekte der Feldtheorien sollen als Erwartungswert-Felder der kleinsten im HKM betrachteten Objekte im Sinne der schon vorn erwähnten „mean-field“-Theorien interpretiert werden. In einfachen Fällen sind die auftretenden zufälligen Größen voneinander unabhängig. Wenn beispielsweise annähernde makroskopische Homogenität des HKG vorausgesetzt wird, ist es unwichtig, in welche Richtung wir schauen, überall werden die gleichen Eigenschaften erwartet und das Medium ist deshalb auch isotrop. Dann sind die zufällig zu ermittelnden Flugwinkel und der Geschwindigkeitsbetrag als unabhängig voneinander anzunehmen. In einem solchen Gas kann vereinfachend angenommen werden, dass parallele Flugbahnen gleich wahrscheinlich sind. Auch die Stoßachsenwinkel können dann als von anderen unabhängige zufällige Größen angesehen werden. Deren Wahrscheinlichkeitsverteilungen ergeben sich dabei geometrisch. Einfach ist die Verwendung von in Computer-Algebra-Systemen eingebauten Zufallsgeneratoren. Beispielsweise in Mathcad liegen solche für viele eindimensionale Wahrscheinlichkeitsverteilungen vor, aber nicht direkt für die Winkelwahrscheinlichkeiten.

Der Erzeugung beliebiger eindimensionaler Zufallszahlen gemäß einer bekannten Wahrscheinlichkeitsdichte liegt nun folgende Idee zugrunde:

Das Integral über den gesamten Definitionsbereich muss 1 ergeben. Gleichmäßig verteilte zufällige Zahlen zwischen Null und 1 kann man durch die Fkt. rnd(1) erzeugen. Diesem Wert kann auch ein bestimmtes Integral von 0 bis x zugeordnet werden, was durch Gleichsetzen erfolgt. Nun wird die Gleichung nach der Variablen x aufgelöst und ergibt somit den gewünschten Zufallsgenerator.

Probiert werden soll dies zuerst für einen zu erzeugenden Stoßachsenwinkel im dreidimensionalen Raum, wo nach (15) aus "B_stoss.pdf" gilt:

(18)

also

(19)

und (18) ist demnach Verteilungsfunktion, weil sie monoton bis ∏/2 wächst. Es gilt

(20)

und damit wird der Zufallsgenerator:

(21)

Für den Drehwinkel der Stoßachse ergibt sich einfach:

(22)

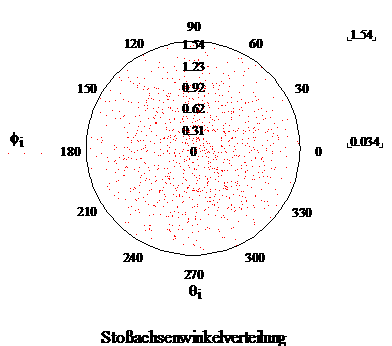
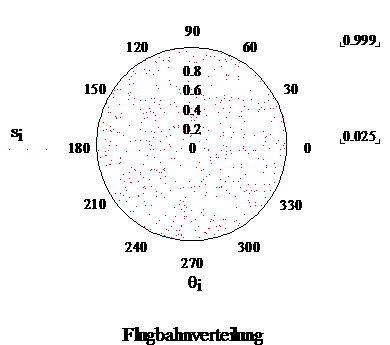
Mit 1000 zufällig erzeugten Punkten ergeben sich beispielsweise folgende Abbildungen:

Abbildung 5:

Abbildung 6:

Zu sehen ist deutlich, dass im mittleren Bereich der Kugeloberfläche mehr Auftreffpunkte liegen, obwohl die Flugbahnen ganz gleichmäßig verteilt sind.

Interessant ist die Abhängigkeit der Kollisionswinkel ф von den Relativgeschwindigkeits­verteilungen, welche vorerst vereinfacht unabhängig von diesen als N(0,1) verteilt, angenommen werden sollen. Die bedingte Wahrscheinlichkeitsdichte für das Auftreffen eines Punktes aus einem bestimmten Winkel auf die betrachtete Probekugel ergibt sich deshalb aus dem Produkt der beiden Wahrscheinlichkeitsdichten mit der verschobenen Verteilung der Relativgeschwindigkeit (vgl. Brendel_stoss.pdf Abbildung 1). Das drückt sich in den hier (aus Symmetriegründen vorerst) interessierenden zwei Dimensionen durch die vereinfachte Wahrscheinlichkeitsdichte:

(23)

aus. Diese kann leicht grafisch dargestellt werden (Abbildung 7), wobei die Asymmetrie der Winkelwahrscheinlichkeiten erkennbar wird.

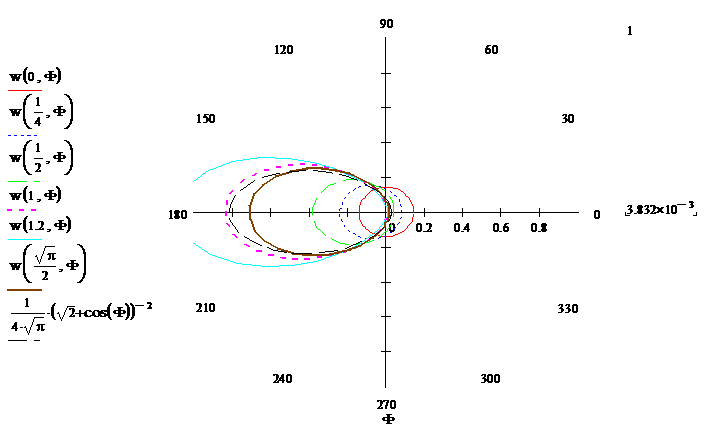
Abbildung 7: Asymmetrie der Herkunftswinkel-Wahrscheinlichkeit

Damit kann nun eine Wahrscheinlichkeitsverteilung für den Winkel ф (vgl. Abbildung 8) hergeleitet werden:

(24)

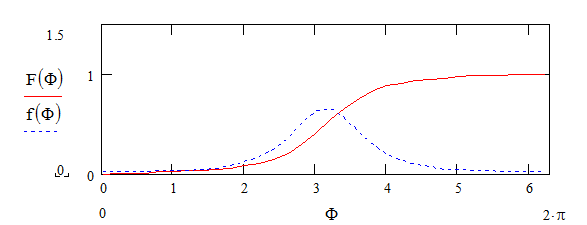
Nach ф lassen sich diese und vorkommende kompliziertere Wahrscheinlichkeitsverteilungen schwer auflösen. Zufallsgeneratoren können jedoch mit Hilfe der Lösungsmöglichkeit für implizite Funktionen konstruiert werden:

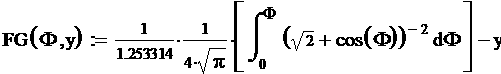(25)

Diese lässt sich mit der im CAS eingebauten root-Funktion für beliebig viele zufällig mit rnd(1) erzeugte Funktionswerte y lösen. Hier wurden beispielsweise 10 Winkel zufällig erzeugt:

(26)

Leider ist eine Simulation von vielen Kugelstößen mit solch einem Zufallsgenerator für wichtige Eigenschaften des Gases zu den Zeitpunkten der Stöße sehr rechenintensiv. Erhöht wird dieser Aufwand noch durch die ständige Notwendigkeit von Anpassungen der Parameter vorkommender Wahrscheinlichkeitsverteilungen durch Mittelwertbildungen. Am wichtigsten für die erstrebte Erweiterung der Standardphysik ist die sinnvolle Zuordnung von Eigenschaften des HKG zu den bewährten Beschreibungsmethoden mit Hilfe von Tensoren und Spinoren. Im DOM können damit anschaulich Phänomene beschrieben werden, für die sonst nur unanschauliche komplizierte mathematische Methoden herangezogen werden. Den Wahrscheinlichkeitsstromflüssen, welchen weiter unten Stoßfrequenzraumwinkeldichten von Mittelwertfeldtheorien zugeordnet werden, können konkret Bewegungen diskreter Objekte entsprechen, seien das nun harte Kugeln oder Strings, Branen, Quantenschaum, Ätheratome oder jetzt auch Knotenstränge (strands). Deren Beschreibung mit teilweise mehrdimensionalen Theorien wird hiermet eine einfache drei plus eindimensionale Interpretation zugeordnet. Mit diesem Hilfsmittel ergibt sich dabei eine Verbindung zu den Beschreibungen des Standardmodells, wie beispielsweise den in Feynman-Prpagatoren verwendeten Erzeugungs- und Vernichtungsoperatoren (z.B. [BD-F 90] 13.6).

Bevor die enorme Aufgabe in Angriff genommen werden sollte, zu bekannten Strukturen der Standardphysik Theorien zu entwickeln, welche die direkte Zuordnung der hier diskutierten kleinen Objekte (harter Kugeln) ermöglicht, ist es erst einmal sinnvoll, zu untersuchen, ob die elementarsten Eigenschaften der physikalischen Natur in einem Gas harter Kugeln überhaupt möglich sind?