Struktur und Dynamik der Materie im

Uratom-Modell

4.3 Quantenhaftigkeit im HKG

 

"Ursache sowohl der Quantenhaftigkeit mikrophysikalischen Geschehens als auch der Gültigkeit von Unschärferelationen für die gleichzeitige Messung komplementärer physikalischer Größen ist im wesentlichen die Existenz des planckschen Wirkungsquantums h" (siehe Stichwort Quantentheorie in [M 73]). Wie ist nun diese Größe im hier betrachteten Medium  zu verstehen? Das Gas muss nicht einmal unbedingt durch das Uratom-Axiom definiert sein. Auch kleinste Objekte, wie Strings, Branes oder sonstige Objekte mit unbekannter Struktur, wie die der Quintessenz, sind möglich. Wichtig ist nur deren geradlinige Bewegung bis zur Berührung eines anderen solchen Objektes und dann ein Geschwindigkeitstausch parallel zur Berührpunktnormale. Dieser Vorgang liegt außerhalb von Standardmodell sowie Allgemeiner Relativitätstheorie und lässt somit alle darin verwendeten Theorien unverändert in deren Gültigkeitsbereich.

 

Eigenschaft h in der Grundmenge:

 

Ausgehend von der Vorstellung eines gewöhnlichen Gases harter Kugeln lässt sich das HKG als Medium betrachten, welches überall vorhanden ist und die grundlegenden Eigenschaften im Mikrogeschehen unterhalb der Elementarteilchen beeinflusst. Aus der statistischen Thermodynamik ist bekannt, dass sich durch Fluktuationen schnell Dichte- und Geschwindigkeitsschwankungen ausgleichen. Die Durchschnittswerte von Geschwindigkeit und Anzahldichte bleiben aber erhalten. Bekannt ist auch, dass sich mit den Größen Masse, Geschwindigkeit und (Wellen-) Länge eine neue Größe mit der Einheit einer Wirkung definieren lässt.

 

Der Begriff Masse ist so grundlegend, dass er hier gleich von vornherein betrachtet werden soll. In der Umgangssprache und auch früher in der Physik wurde unter Masse einfach die Anzahl verstanden. Das soll hier verwendet werden. Generell bieten sich dabei zwei verschiedene Möglichkeiten an.

 

Erstens sind von vornherein tatsächliche Messwerte verwendbar und das Vakuum bleibt masselos, dafür besteht aber das Problem, dass die zu verwendenden Zahlenwerte nicht einzelnen Grundobjekten zugeordnet werden können, weil bei unseren heutigen Messungen die wahren Größenordnungen der Urmaterie nicht in Erscheinung treten. Diese Betrachtungsweise entspricht der, wie sie in den meisten Theorien angewandt wird, die von messbaren Phänomene ausgehen.

 

Zweitens kann jedem, noch hypothetischen, elementaren Objekt die Masse 1 zugeordnet werden. Bei diesem Standpunkt muss der leere Raum auch eine gewisse Masse und somit Energie besitzen. Ein gewisser Grenzbereich für solche Systeme ist die Größenordnung der in dem System vorkommenden freien Weglänge. Systemkugeln müssen aber nicht wirklich auf diesen Bereich beschränkt sein. Wegen des Stoßgleichgewichts verschmieren sich die Orte der Systemkugeln praktisch bis ins Unendliche. Da nur Zufallswerte untersucht werden können, ist demnach das Integral der Normalraumabweichung über den gesamten Raum, welches sich kaum vom Absolutwert im Vakuum unterscheidet, zu verwenden. Hier soll dieser neue Weg gegangen werden.

 

Deshalb gilt mit der Anzahl N gemeinsam in einem angenommenen System betrachteter Kugeln für deren Masse: m := N. Mit der Anzahldichte (= Teilchenzahldichte) n = N / V, dem Kugeldurchmesser d, der freien Weglänge L und der Geschwindigkeit einer Kugel vi gilt dann:

 

 

 

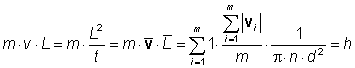
Die als plancksches Wirkungsquantum zu interpretierende Größe h ist unabhängig von der Größe des betrachteten Systems. Wird ein unendlich ausgedehntes äußeres System (Universum) betrachtet, in dem andere eingebettet sind, erfolgt durch die anwendbaren Gesetze der Thermodynamik, die als effektive Theorie keine Details wie Stoßachsenwinkel oder Vektorwinkel betrachtet, durch Dichtefluktuationen normalerweise eine Anpassung der Eigenschaften. Es stellen sich schnell lokale Stoßgleichgewichte ein. Der Teilchenfluss durch eine kleine Fläche bleibt in einem größeren Zeitintervall konstant. Dadurch ergibt sich in den Systemen, nach der gleichen Formel, weil h konstant ist, durch einfache Auflösung nach L:

 

,

 

was die bekannte Compton-Wellenlänge für alle Materie beschreibt. In den beobachtbaren Phänomenen zeigt sich diese Verknüpfung dadurch, dass kleinere Systeme (Elementarteilchen) mit größerer Masse (bzw. Energie) verbunden sind und größere Systeme mit kleinerer Masse (bzw. Energie). Für den Begriff Größe sind unterschiedliche Interpretationen möglich und auch gebräuchlich. Einerseits kann damit die tatsächliche Ausdehnung zusammen hängen, was in Streuversuchen überprüfbar ist, andererseits kann diese als Unschärfe bei der Messung interpretiert werden. Gegen die Interpretation einer Erzeugung des planckschen Wirkungsquantums durch die Dynamik der Elementarteilchen selbst, also ohne kleinere Bestandteile, die auch im Vakuum vorkommen, sprechen die gleichen beobachteten Zusammenhänge bei sehr unterschiedlichen Systemen wie Lichtquanten mit sehr großer Wellenlänge und  andererseits sehr energiereicher Makroteilchen mit kleiner Wellenlänge und ähnlichen beobachtbaren Erscheinungen (z.B. Interferenz).

 

Über die notwendige Stabilität der Systeme im betrachteten HKG wird hier noch nichts gesagt. Sie werden aus Objekten gebildet, die ihre inneren Strukturen durch Strings, Branes, Quantenschaum oder eben auch harte Kugeln erhalten können und auch über längere Zeit stabil bleiben. Für die Existenz der Größe h reicht die Annahme der Existenz solcher kleineren Objekte als diejenigen, die im Standardmodell und der Gravitation in Erscheinung treten. Deren Betrachtung, ähnlich wie in der statistischen Physik, führt dann zur konstanten Eigenschaft h,  welche das gesamte Mikrogeschehen beeinflusst. Falls die einführende Behauptung als wahr akzeptiert wird, wäre damit schon der Nachweis der Quantenhaftigkeit erbracht. Welcher Unterschied ergibt sich aber zwischen der statistischen Thermodynamik und dem hier betrachteten HKG?

 

Vergleich von Thermodynamik und HKG-Dynamik

 

Wegen der Annahme eines gasähnlichen Mediums zur Erklärung elementarer Erscheinungen, welche vom Standardmodell und der ART beschrieben werden können, ist es sinnvoll, wo möglich Methoden der Thermodynamik oder Akustik, die auf solchen aus der statistischen Physik beruhen, anzuwenden. Energie- und Impulserhalt bei Stößen im HKG sind schon vorn (4.2 Geschwindigkeiten, Winkel und Dichte in gegenseitiger Abhängigkeit) gezeigt worden. Im späteren Verlauf sind nähere Untersuchungen zu weiteren Zusammenhängen geplant. Hier sollen deshalb nur einige Besonderheiten tabellarisch gezeigt werden:

 

statistische Physik

Anwendung

HKG-Dynamik

 

Atome, Moleküle

 

1. kleinste Objekte

allgemeine Objekte

(Strings, Branes, Quintessenz, Spinschaum, harte Kugeln,...)

 

meist Vielfaches der freien Weglängen

 

2. Größenordnung

 

auch kleiner als durchschnittliche freie Weglänge

 

Schallwellen

(longitudinal)

 

3. Störungsausbreitung

 

elektromagnetische Wellen (transversal)

 

 

4. Stoßgleichgewicht mit Umgebung

 

Turbulenzen und Wirbel bisher nicht ohne Zusatzkräfte

 

5. Systeme

 

Elementarteilchen, benötigen zur Beschreibung wirbelartigen Spin

 

nicht beobachtet

 

6. Quantelung

Zustandsänderungen gequantelt wegen Stoßgleichgewicht zur Umgebung

Potenzial zwischen Teilchen

und

Strömungsmischung

 

7. Wechselwirkungsursache

potenzialfreier Geschwindigkeitstausch und Strömungsmischung

statistische Momente aus

Anzahldichte und Geschwindigkeiten

 

8. wesentliche Einflüsse

Vektor- und Stoßachsenwinkel, Anzahldichte und Geschwindigkeiten

 

Energie- und Impulserhaltung

 

 

9. bekannte Phänomene

 

Energie- und Impulserhaltung

 

 

Entropieabnahme

 

 

10. wichtigstes Phänomen

Entropie

Ω = Mikrozustand aus Orten und Impulsen, kB = Boltzmannkonstante

 

für Systemerhalt: Entropiezunahme

(noch zu beweisen)

 

Standardmodell + ART

 

 

11. Theorie

 

Allumfassende Theorie (TOE)

 

In der statistischen Physik und den abgeleiteten klassischen Theorien taucht die Größe h nicht auf. Die hier versuchte Erweiterung von Standardmodell und ART durch die Annahme eines Mediums gemäß dem Uratom-Axiom muss auch die Beschreibungsmethoden der Quantentheorie umfassen. Damit sollten alle bewährten Quantisierungsmethoden anwendbar sein.

 

Anwendung der Größe h zur Quantisierung

 

Vorausgesetzt wird die Beschreibbarkeit von bestimmten Erscheinungen durch die verschiedensten Theorien. Diese verwenden je nach Zweck mathematische Konstrukte wie Räume in verschiedenen Dimensionen, Gruppen, ... Solche Theorien müssen nun zur Beschreibung des gesicherten Auftretens der mit dem planckschen Wirkungsquantum zusammenhängenden Portionsgrößen in Einklang gebracht werden. Dazu ist eine Quantisierung erforderlich. Dazu ist in diesem Modell keinerlei neue Idee erforderlich. Alle verschiedenen Quantisierungsmethoden (z.B. laut Wikipedia: kanonische Quantisierung, Pfadintegral, geometrische Quantisierung, Bohr-Sommerfeld-Quantisierung, 1. Quantisierung, 2. Quantisierung, Deformationsquantisierung), verwenden mit unterschiedlichen Ansätzen die grundsätzliche Größe h und sind deshalb wie im Standardmodell verwendbar. Eine Anwendung auf die ART kann allerdings erst nach einem zusätzlichen Gedanken (Diskretisierung) erfolgen. Von den Methoden wird hier nur die kanonische Quantisierung etwas näher betrachtet.

 

Eine bekannt physikalische Erkenntnis ist die vollständige Beschreibbarkeit eines dynamischen Systems durch die beiden Größen Ort und Impuls. Als mathematisches Hilfsmittel wurde später der Phasenraum eingeführt und in diesem ein mechanisches System durch die hamiltonsche kanonische Theorie umfassend beschrieben. Die hier bisher verwendete Methode ist mit dieser wegen der obigen Massendefinition identisch. Die auftretenden Poissonklammern (vgl. z.B. [S 89] S. 398f)

 

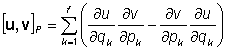
sind anwendbar, wenn die Objektdurchmesser verschwinden können und wenn verschiedene Teilchenmassen auftreten. Weil die Uratome (bzw. allgemeiner die betrachteten Objekte) eine Ausdehnung besitzen und somit keine zwei elementaren Impulse gleichzeitig am selben Ort vorkommen, kann diese Poissonklammer um einen Faktor erweitert werden, der das Stoßgleichgewicht zur Umgebung gewährleistet. Das ist gerade der Faktor h. Die nun groß geschriebenen Operatoren im Kommutator werden auf etwas angewendet, das jetzt allgemein als eine Beschreibung von Urmaterie oder Psi-Materie aufgefasst werden kann. Mit der Vorstellung, dass es sich um ein diskretes Etwas handelt, wird durch den Faktor h gewährleistet, dass zwischen beiden zu betrachtenden Zuständen ein Stoßgleichgewicht herrscht. Damit ergibt sich die Ersetzung:

 

Eine so beschriebene Materieportion muss sich nun als offene Menge aber nach dem Grundmengenaxiom und auch nach der Erfahrung im ständigen Gleichgewicht mit seiner Umgebung befinden. Deshalb tritt bei einem Übergang zwischen zwei Zuständen die Größe h auf, welche ja nur die Erwartungswerte des Normalraumes charakterisiert. Diese ist bei Stößen als Durchschnittswert invariant. Das ist der Hauptinhalt aller Quantisierungen beliebiger ansonsten klassischer Theorien. Aus der Poissonklammer wird so zwangsweise ein Kommutator

1/ iħ [F ,G]. F und G sind hier die hermitesierten Operatoren F und G (Observablen).

Daraus folgen für N Quantenteilchen (K,L = 1,2,...,3N) die heisenbergschen Vertauschungsrelationen

 

wobei die QK und PL die kanonisch konjugierten Lage- bzw. Impulsoperatoren sind. Dies gilt auch als allgemeine Vorschrift zur Quantisierung zweier beliebiger kanonisch konjugierter Observablen, deren physikalische Bedeutung offengelassen werden kann. Die Wellengleichung des klassischen Wellenfeld-Bildes wird auf die gleiche Art durch Multiplikation mit h zur Wellengleichung für ein freies Teilchen (System von Uratomen) bzw. zur zeitabhängigen Schrödinger-Gleichung.

Der von Schmutzer (vgl. [S 89]) beschriebene Weg über die Wirkungsfunktion der kanonischen Mechanik (S. 407), bzw. die zeitabhängige Hamilton-Jakobi-Gleichung (S. 408) und die Wärmeleitungsgleichung (S. 985), welche ja ein vorstellbares System von stoßenden Teilchen beschreibt, führt ebenfalls zur Schrödinger-Gleichung (S. 1277), nur dass jetzt auf der tieferen Stufe der Uratome (bzw. allgemeineren kleinen Objekte) die Zusammensetzung einer durch diese beschriebenen Materieportion deutlich wird. Auch für das Auftreten von Antikommutatoren zeichnet sich wegen der inneren Selbstwechselwirkung in Fermionenfeldern eine anschauliche Erklärung ab (vgl. [BD-F 90] S.62). Es wird auf herkömmliche Art der gesamte Formalismus der Quantenmechanik erschlossen und unter Einbeziehung der eigentlich schon enthaltenen, aber noch zu zeigenden Lorentz-Invarianz die gesamte Quantentheorie.

Beispielsweise kann man die unendlichen Matrizen der Quantenmechanik, welche den zweifachen unendlichen Mannigfaltigkeiten entsprechen, wie sie in den Fourierreihen zur Approximation von periodischen Funktionen der Wellenmechanik verwendet werden, besser interpretieren, wenn man sich eine mögliche Zuordnung zu kleineren Objekten vorstellt. Die Frequenzen gehören jeweils zu zwei Zuständen und die bereits vorn erwähnten Minischwingungen stellen gerade die im Normalraum mit der Eigenschaft h bzw. bei Kreisprozessen mit ħ zulässigen Übergänge, also Urmaterieflüsse, dar. Das Auftreten der komplexen Größe i hat neben der reinen mathematischen Zweckmäßigkeit, welche durch die häufige Betrachtung zweier Zustände (z.B. immer orthogonal betrachtete Zeit) oft zweckmäßig ist, die Aufgabe, im Rahmen der in der Grundmenge stattfindenden Selbstwechselwirkung, im mathematischen Formalismus Ordnung zu schaffen. Wie alle mathematischen Hilfsmittel erfüllen die Komplexität, mehr als drei Raum-Dimensionen (z.B. der Phasenraum oder  Hilbertraum) und andere mathematische Strukturen nur die Aufgabe einer erleichterten Beschreibungsmöglichkeit der durch das Standardmodell und die ART beschreibbaren Phänomene. Erst die Annahme von Objekten außerhalb dieser Theorien versucht eine Erklärung und Zuordnung zu echter physikalischer Realität.

 

 

Atomistische Diskretisierung von Wahrscheinlichkeiten und Potenzialen

 

Die Größe h muss somit im Rahmen des bewährten Formalismus der theoretischen Physik als charakteristische Eigenschaft für den normalen Uratomfluss (bzw. allgemeiner den Fluss der kleinsten Objekte) angesehen werden. Sie ist gleichzeitig das Maß für eine Minischwingung mit der freien Weglänge (diese könnte als String, also Saitenschwingung interpretiert werden). Bei größerer Masse, d.h. größerer Zahl der beteiligten Kugeln in einer elementaren Raumzelle, wird die freie Weglänge kürzer. Bei größerer Geschwindigkeit des betrachteten Systems erfolgt eine adäquate Änderung der Systemlänge, was im Rahmen der relativistischen Betrachtung verständlich werden soll. Das Stoßgleichgewicht zum umgebenden Raum ist eine Bedingung dafür, dass Systeme sich durch Dichtefluktuation nicht schnell auflösen. Mindestens eine zusätzliche geometrische Eigenschaft muss aber hinzu kommen, die das statistische Verhalten der Fluktuation kompensiert. Das soll der später zu behandelnde Systembildungseffekt werden.

Wie schon erwähnt, können im Rahmen der physikalischen Beschreibung des Naturgeschehens unterschiedlichste, aber trotzdem richtige Theorien entwickelt werden. Die Zahl annähernd gleichwertiger Theorien im Rahmen des Standardmodells ist so groß, dass hier nicht näher darauf eingegangen werden kann. Eine wesentliche Gemeinsamkeit, auch mit der noch nicht quantisierten ART ist jedoch das Auftreten kontinuierlicher, "verschmierter", sich wandelbarer Materie. Die Elementarteilchen können sich unter  gewissen Bedingungen vielfältig ineinander umwandeln. Auch die Quantisierung ändert nichts daran, dass im Standardmodell und in der ART zur Beschreibung dieses Verhaltens kontinuierliche Funktionen verwendet werden müssen, die unendlich feine Zerlegungen zulassen. Das Uratom-Axiom verlangt aber eine diskrete atomistische Beschreibbarkeit dieser kontinuierlichen Funktionen. Da alles, was wir in den Computer eingeben intern in diskrete Teile zerlegt wird, ist das natürlich auch mit den verwendeten Funktionen möglich.

Speziell können mit Wahrscheinlichkeitsverteilungen Zufallsgeneratoren konstruiert werden, die einzelne bewegte Objekte erzeugen. Oft lassen sich zwar solche Funktionen nicht so auflösen, dass eine Zuordnung aus einem gleichverteilten Zufallsgenerator, der Zahlen zwischen Null und Eins liefert, möglich wird. Dann kann die in Computeralgebrasystemen oft vorhandene root-Funktion trotz allem noch numerische Werte liefern. Diese können dann z.B. in Simulationen so weiter verwendet werden, dass eine Aussage über das Verhalten der damit beschriebenen Menge kleinster Objekte möglich wird. Die Anzahl der generierten Objekte muss natürlich Masse bzw. Impuls oder Energie des betrachteten Systems ergeben und liefert wohl nur auf aller niedrigster Stufe einer Feinauflösung der mathematischen Konstrukte sinnvolle Ergebnisse. Noch immer bewegt man sich damit aber im Rahmen des Standardmodells und die Massen müssen aus den Versuchsergebnissen hinein gesteckt werden.

Zur Messung ist pro Größe ein Zusammenstoß der zugehörigen Objekte (Kugeln) erforderlich. Diese Objekte können sich wegen ihrer Ausdehnung nicht gleichzeitig am gleichen Raumpunkt befinden. Es muss immer eine ganze Menge, sich ja mit dem umliegenden Raum in einem gewissen Stoßgleichgewicht befindende, Kugeln zum Zusammenstoß mit einem bekannten Kugelmengensystem gebracht werden. Das lässt sich als Aufsammlung der Ergebnisse von vielen Elementarereignissen interpretieren. Dabei auftretende Übergänge zwischen zwei Zuständen können deshalb immer nur mit der Unschärfe h erfolgen.

Zusammenfassung

 

Offensichtlich wird bei Stößen die Flugrichtung sehr stark verändert. In der neuen Richtung ist wieder ein Stoß entsprechend der vorhandenen Anzahldichte im Moment des Erreichens eines bestimmten Ortes zu erwarten. Die Ermittlung der zugehörigen lokalen Wahrscheinlichkeit wird allerdings schwierig. Trotzdem sind auch ohne diese einige Aussagen möglich.

Wegen des offenen Systems stellt sich in einem beliebigen Raum-Zeit-Intervall ein gewisses Gleichgewicht gegenüber der Umgebung ein, wenn es sich um ein für längere Zeit stabiles System handelt. Bei einer durch einen Zusammenstoß zufällig erzeugten Geschwindigkeitsabweichung gegenüber dem Normalraum wird gleichzeitig die entsprechende freie Weglänge bis zum nächsten Zusammenstoß verändert. Eine schnellere Kugel fliegt weiter, eine langsamere weniger weit. Die Summe der freien Weglängen zweier aufeinander zu fliegender Stoßpartner ändert sich dabei normalerweise, was zu einer Dichtefluktuation führt und der Effekt des Systemerhalts muss erklärt werden. Die Geschwindigkeits-Betrags-Summe und die Anzahldichte ändern sich stoßabhängig, aber es können und müssen Grenzwerte erreicht werden, weil es keine größere als maximale Auffüllung des betrachteten Systembereichs geben kann. Die Stoßtransformationen ändern aber weder Energie noch Impuls in dem betrachteten System. Diese können lediglich auf andere Uratome verlagert werden. In der gesamten betrachteten Menge von stoßenden Kugeln bleiben deshalb ständig alle damit ableitbaren (thermodynamischen) Zustandsgrößen konstant. Einschließlich der Größe h.

Zusammenfassend kann hier konstatiert werden, Quantenhaftigkeit bedeutet im Sinne der historischen Entwicklung

 

Bewegung ist nicht quantisierbar, weshalb z.B. auch Photonen mit allen möglichen Wellenlängen durch den Doppler-Effekt erzeugt werden können. Impuls und Energie können im gesamten kontinuierlichen Spektrum auftreten. Ebenfalls nicht quantisiert werden können im normalen Sinne das klassische elektrische und magnetische Feld. Virtuelle "Quanten" sind dazu nötig. Auch bei den virtuellen Quanten der Wechselwirkungstheorien verhält es sich ähnlich. Die Beobachtung und damit "Realwerdung" ist erst bei Energien möglich, die ein Stoßgleichgewicht zur Umgebung ermöglichen und das können auch für Teilchenbeschleuniger noch unerreichbare Energien sein.

 

 

Die Quantenhaftigkeit des mikrophysikalischen Geschehens ist nach dem Gezeigten wie gefordert eine natürliche Folge des Uratom-Axioms. Wenn man kurzfristig die angebotene Erklärungsmöglichkeit und die damit erreichbare Anschaulichkeit der Größe h vergisst, ergibt sich überhaupt nichts Neues gegenüber dem Standardmodell und der ART. Für die daraus erstrebte Entwicklung einer Allumfassenden Theorie (AUT bzw. Theory Of Everything) ist eine Angabe der Uratomgröße erforderlich. Unter Annahme des tatsächlichen Vorhandenseins des HKG, ist bei bekanntem, sehr genau ermitteltem h zunächst aber die Durchschnittsgeschwindigkeit in diesem Gas harter Kugeln zu ermitteln. Wie wirkt dann damit das thermodynamische Verhalten auf die Struktur von Raum und Zeit? Das soll nun im nächsten Teil kurz untersucht werden.

Literatur:

[BD-F 90] Bjorken, J.D., Drell, S.D.; Relativistische Quantenfeldtheorie; Mannheim, Wien, Zürich 1990
[M 73] Meyers Physik-Lexikon; Mannheim, Wien, Zürich 1973
[F 89] Fachlexikon ABC Physik; 2 Bde; Thun, Frankfurt/M, 1989
[S 89] Schmutzer, E.; Grundlagen der theoretischen Physik, mit einem Grundriß der Mathematik für Physiker; 2 Bde Mannheim, Wien, Zürich 1989
[G 85] Grawert, G.; Quantenmechanik; Wiesbaden 1985
 
 

 Inhalt 

 Grafik 

 vorheriges 

 nächstes 

 Links 

Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.de, Porec/ Sarajevo 2000 - 2006
Uratom (Anfang)