Struktur und Dynamik der Materie im
Uratom-Modell
4.2
Geschwindigkeiten, Winkel und Dichte in gegenseitiger Abhängigkeit
(ursprünglicher
Text =>)
Diese
Betrachtungen hier sind Schlüssel für das gesamte angestrebte
Modell. Es wird ja nichts anderes betrachtet, als die Vorgänge bei
massenweisem Vorkommen von einfach zu beschreibenden Stößen,
welche die einzige Selbstwechselwirkung in dem HKG darstellen. Die
Selbstwechselwirkung kann immer auf einen Zweierstoß
zurückgeführt
werden. Aus der Stoßformel folgt nun durch einfaches Einsetzen
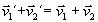
Der Beweis dieser Aussage ist
auch mit den ausführlicheren 3-dimensionalen
Stoßtransformationen Teil der näher untersuchten Stoßfälle.
Da im ursprünglichen
sowie im gestrichenen (neuem) System auch die Annäherungs- und
Entfernungsgeschwindigkeitsbeträge übereinstimmen, gilt
dies ebenfalls für die daraus bildbaren Quadrate. Durch
Induktionsbeweis lässt sich damit zeigen, dass auch in der
Grundmenge mit Selbstwechselwirkung Impuls- und
Energieerhaltungssatz
gemäß der natürlichen Vorstellung gelten. Wichtig ist auch die damit geltende Erhaltung der Schwerpunktsbewegung
in abgeschlossenen Systemen betrachteter Uratome.
Das darf aber nicht darüber hinweg
täuschen, dass
bei den Zusammenstößen im allgemeinen die Summen und
Differenzen der Beträge von Einzelgeschwindigkeiten verändert
werden, was bei einem rechtwinkligen
Zusammenstoß, bei dem eine Kugel praktisch zur Ruhe gebracht
werden kann und
die resultierende Geschwindigkeit der anderen nach dem Satz von
Pythagoras nur
den Betrag der Hypotenuse erhält, am leichtesten einzusehen ist. Durch
diese Veränderungen werden Systembildungen erst denkbar, wenn
sich die
unterschiedlichen Komponenten massenweise in verschiedenen,
zusammengehörenden
Teilmengen der Grundmenge, d.h. in Systemen befinden.
Elementare
Eigenschaften der Grundmenge sind die Anwesenheit und die Bewegung der
Uratome an Raum-Zeit-Punkten. Wegen der notwendigen
Wahrscheinlichkeitsbetrachtung wird angenommen, dass diese durch die
Dichte- und Geschwindigkeitsverteilung genügend genau beschrieben
werden können. Welchen Einfluss haben aber nun die möglichen
Vektorwinkel und vielleicht die Stoßachsenwinkel auf diese
Wahrscheinlichkeitsverteilungen? Das wird in Winkelwahrscheinlichkeiten.htm
mit Mathcad näher, aber noch nicht umfassend, untersucht.
Die
Geschwindigkeits-Normalverteilung und auch die lokale Anzahldichte
verändern sich bei Stößen normalerweise lokal, also
zumindest in der näheren Umgebung.
Kugelmengenflüsse mit schmalerer oder breiterer
Geschwindigkeitsverteilung und von
der
Durchschnittsgeschwindigkeit abweichendem Erwartungswert sind
möglich. Die Stoßhäufigkeit
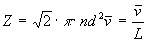
bestimmt den erwarteten Uratom-Fluss durch
eine
interessierende Fläche. Deshalb ist es notwendig, einen
Zusammenhang mit den
vorn betrachteten Wahrscheinlichkeiten für das Auftreten von
Vektor- und
Stoßachsenwinkeln einzubeziehen. Bei einer entsprechenden
Vektordarstellung lassen
sich möglicherweise die Erwartungswerte direkt einsetzen. Eine
exakte
Untersuchung soll jedoch der vorgeschlagenen Elementarteilchentheorie
vorbehalten bleiben. Etwas ausführlicher werden diese Gedanken
aber auch
später bei der Diskussion der Elementarteilchen und
Wechselwirkungen behandelt.
Interessant
werden hier Überlegungen, dass die
Stoßhäufigkeit von der
erwarteten Aufenthaltszeit in einem bestimmten Raumbereich
abhängt. Diese ist
zwar umgekehrt proportional zur (Relativ-)Geschwindigkeit der
betrachteten
Kugeln, die Stoßzahl Z erhöht sich aber proportional zu
dieser. Die freie
Weglänge ist dabei geschwindigkeitsunabhängig.
Für den Aufbau der Welt aus Uratomen wichtige Zusammenhänge
zwischen den
elementaren Eigenschaften einer Uratomansammlung und deren
Stoßverhalten seien
deshalb in Stichworten zusammengefasst:
- Die Geschwindigkeitssumme
vor einem
Stoß ist gleich der Summe nach dem Stoß.
- Der
Annäherungsgeschwindigkeits-Betrag ist gleich dem
Entfernungsgeschwindigkeits-Betrag, auch nach einem Stoß, d.h.
der Relativgeschwindigkeitsbetrag und auch dessen Quadrat ändern
sich bei Stößen nicht. => Impuls und Energieerhaltung
- Die
Geschwindigkeits-Betrags-Summe ist nach frontalen Stößen
meistens
größer als vorher. => Entropie?
- Die Geschwindigkeits- Betrags- Differenz
ist nach frontalen Stößen meistens kleiner. Bei
Frontalstößen passen sich die Geschwindigkeitsbeträge
an. => konstante Lichtgeschwindigkeit?
- Das normale Vakuum
(Normalraum) ist möglicherweise ein sehr dünnes Medium mit
vielen vorkommenden Frontalstößen, bei denen sich die
Geschwindigkeiten an die Durchschnittsgeschwindigkeit anpassen.
- Bei
Querstößen, also häufigen Fällen im homogenen
Gas, ergibt sich oft
eine Absolutgeschwindigkeits-Betrags-Abnahme und
Anzahldichte-Zunahme. => möglicherweise Systembildung. Nach einem Stoß,
bei dem die Geschwindigkeits-Betrags-Summe kleiner wird, nimmt
die Anzahldichte
zu, weil
nach einem festen Zeitintervall die Entfernungssumme vom
Stoßpunkt kleiner ist als im gleichen Zeitintervall vor dem
Stoß, d.h. wenn die Kugeln nahe aneinander vorbei fliegen
würden.
Die
Anzahldichtezunahme und damit selbständige Materieansammlung in
einer
chaotischen Menge stoßender Kugeln stehen im Widerspruch zur
landläufigen
Meinung und es ist unklar, ob darüber schon berichtet wurde?
Diese Erkenntnisse
wurden noch ohne detaillierte Untersuchungen des Einflusses
unterschiedlicher Dichte auf das Vorkommen verschiedener Winkel
gewonnen. Als wichtigste Eigenschaft im betrachteten HKG muss das aber
systematisch erfolgen. Derzeitige Anfangsüberlegungen zu den
Winkelwahrscheinlichkeiten und frühere Vermutungen
über häufige Frontalstöße müssen demnach
systematisch erweitert und verbessert werden. Sicher ist aber auf jeden
Fall das Auftreten von gegenseitig
bedingten Wechseln zwischen Dichte und Schnelle beim Schall in
tatsächlich existierenden Gasen. Diese können nur durch
Stöße erzeugt werden und diese beeinflussen die
Stoßwahrscheinlichkeiten (Stoßfrequenzen) in ihrer
Umgebung. Stöße verzerren also die Raumzeit durch die
Selbstwechselwirkung der
elementaren Felder auch an anderen Orten, wo sich momentan kein Uratom
befindet. Anschaulich
vorstellbar wird das durch die mit jeder Bewegung verbundene
Änderung der
Auftreffwahrscheinlichkeit.
Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der
Materie
im Uratom-Modell, http://uratom.de, Porec und Sarajevo 2000-2006
Uratom (Anfang)
![]()
![]()
![]()