U(1)-Symmetrie im Uratommodell

Struktur und Dynamik der Materie im

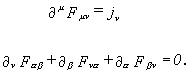
4.5 U(1) - Symmetrie bezüglich Dichte und Geschwindigkeit

(elektromagnetisches Feld)

Trotz der Betrachtung statistischer Größen beschränken sich die Untersuchungen bis hierher praktisch auf einige wenige Kugeln in einer ansonsten gleichmäßig verteilten Anzahldichte und normalverteilten Geschwindigkeit mit überall gleichem Erwartungswert und gleicher Streuung. Durchaus natürlich ist nun, bei Annahme möglicher Abweichungen von den Standardwerten des Normalraumes, die Zuordnung eines skalaren Feldes bzw. Potentials V (Anzahldichtefeld, wobei die Bezeichnung leider in der Literatur nicht der deutschen Abkürzung entspricht) und eines vektoriellen Feldes bzw. Vektorpotentials A (Geschwindigkeitsvektorfeld) zu den Erwartungswerten dieser Abweichungen. Zur Ermittlung von numerischen Werten können in einem Gedankenversuch verschiedene Durchschnittsbildungen verwendet werden. Jedesmal müssen von einem Feldpunkt aus entferntere mit einem kleinen Anteil an Aufenthaltswahrscheinlichkeit berücksichtigt werden. Der umgekehrte Weg ist in der Praxis aber wichtiger. Bei diesem können aus einem gegebenen Feld bewegte Uratome generiert werden. Diese lassen sich dann als Repräsentanten des Feldes in einem stochastischen Prozeß weiter verfolgen. Leider sind im Normalfall nur die Potentiale und damit keine absoluten Feldgrößen in echten Geschwindigkeits- und Dichte- Werten bekannt. Trotz allem müssen aber die in der mathematischen Beschreibung vorkommenden Größen aus dem oben definierten Anzahldichte- und Geschwindigkeitsvektor- Feld gebildet werden.

Wir wissen, daß die Schrödinger-Gleichung bzw. bei hohen (systeminternen) Geschwindigkeiten die Klein-Gordon- oder die Dirac-Gleichung ebenfalls diese Struktur besitzen. Unter Einschluß der Elementarladung e stellen diese Feldgleichungen gerade Portionen von Psi-Materie, d.h. elementare Kugelmengensysteme dar, weil die verwendeten Spinoren und Tensoren auf Stoßgebilde zurückzuführen sind. Deshalb läßt sich die bewiesene Invarianz gegenüber globalen Phasentransformationen y--> exp(ia) y und auch gegenüber lokalen Phasentransformationen
y(x) --> y ´(x) = exp(i a (x)) y (x) zum Beweis verwenden (vgl. z.B. [B 86] S. 64 f.) und damit gilt die Eichsymmetrie U(1) in diesen Teilmengen der Grundmenge, in denen keine Verschiebung des Vektorwinkelerwartungswertes auftritt. Dazu muß das Eichfeld A^mu(x) mit x = {x,t} eingeführt werden, welches als Viererpotential (Geschwindigkeit und Dichte) die natürlichen lokalen Fluktuationen beschreibt. Die Stoßachsenwinkel können dabei beliebige Werte annehmen, ein von Null abweichender Vektorwinkelerwartungswert deutet aber auf eine Ruhmasse der betrachteten Teilmenge hin.

Durch die obige Einführung der Felder V und A in der Grundmenge erhalten auch die einzigen Größen, welche eine Veränderung vorhandener Anzahldichte- oder Geschwindigkeits-Erwartungswerte verursachen, also die Vektor- und Stoßachsenwinkel, eine wichtige Bedeutung als Erzeuger der Abweichungen von den Normalraumwerten. Beispielsweise können den Normalraumeigenschaften deshalb die Werte Null zugeordnet werden. Angenommene systeminnere Abweichungen der Vektorwinkelerwartungswerte von den Normalraumwerten könnten die Drehung des betrachteten (Teil-) Systems verursachen, was noch eingehender untersucht werden muß und sind für die mögliche Dichteabweichung verantwortlich, welche die (Ruh-) Masse beeinflußt. Im dünnen Medium der Grundmenge kann diese Dichteabweichung nur positive Werte, bis zur maximalen Auffüllung des Raumes, annehmen. Die erzeugten freien Felder können dagegen positive oder negative Dichteflüsse mit positiven oder negativen Geschwindigkeitsabweichungen vom Normalraum- d.h. Vakuumserwartungswert sein. Nach den obigen Überlegungen verändert sich dabei jeweils mit der Dichte auch die freie Weglänge. Das Entscheidende für die U(1)- Eichsymmetrie ist in diesem Modell die Eigenschaft, daß sich nach mehreren Frontalstößen, welche im dünnen Medium ja vorwiegend auftreten, wegen der bei jedem Stoß unveränderten Relativgeschwindigkeit, die Geschwindigkeitsbetragsdifferenzen dem Grenzwert Null immer mehr annähern. So erhalten alle, aus dem in der Nähe und ebenfalls nur der U(1)- Symmetrie unterliegenden Raum (Vakuum mit elektromagnetischen Feldern) stammenden, Stoßpartner ungefähr den gleichen Absolutgeschwindigkeitsbetrag.

In diesem bekannten Formalismus (vgl. z.B. [BH 79] ergibt sich die physikalische Zuordnung von elektrischen Feldgrößen E dadurch, daß in dem zu bildenden antisymmetrischen Feldstärketensor
F_{mu nu}= - F_{nu mu} die Größen F₀₁ = E₁, F₀₂ = E₂, und F₀₃ = E₃ gesetzt werden. Dementsprechend werden F₂₃ = B₁, F₃₁ = B₂ und F₁₂ = B₃ die Komponenten der magnetischen Feldstärken , also bekanntlich eines quellenfreien Wirbelfeldes. In dieser 4-Form gelten somit die Maxwellschen Gleichungen im Vakuum

Elektrische Feldstärken entsprechen also einfach dem, in der Uratom-Menge von den Normalraum-Erwartungswerten abweichenden, Geschwindigkeitsvektorfeld. Die Beschleunigungen von Systemen erfolgen dabei durch Einmischung günstiger Feldgrößen aus einem benachbarten System oder dem umliegenden Raum.

Der auftretende Materietransport ist selbstverständlich quellenfrei. Mit ihm sind immer Zusammenstöße von Uratomen verbunden, bei denen wie vorn gezeigt, Annäherungs- bzw. Entfernungsgeschwindigkeitsbeträge erhalten bleiben, deren Richtung aber verändert wird. Diese Verwirbelung ist die Haupteigenschaft des Magnetfeldes. Beim durchschnittlichen 45° Stoßachsenwinkel ergibt sich genau die Drehung von 90°. Nur unter grober Vereinfachung kann die elektrische Feldstärke mit den Geschwindigkeitsvektoren und das Magnetfeld mit dem Uratomtransport identifiziert werden. Zu berücksichtigen ist dabei vor allem noch die wechselseitige Auftreffwahrscheinlichkeitsveränderung.

Das Eichprinzip ist in diesem einfachen Modell durch die Tatsache verwirklicht, daß eine Kugel ungefähr am erwarteten Zusammenstoßpunkt zusammenstoßen wird. Deshalb muß für den mathematischen Ausdruck, welcher die Menge beschreiben soll, zu der das Uratom gehört (System), ein Eichfeld A^mu(x) = (V(x),A(x)) eingeführt werden. Es beschreibt eine lokale Symmetrie, d.h. eine Verschiebung des erwarteten Zusammenstoßpunktes. Mit anderen Worten ist das eine Verzerrung des betrachteten Raumes und bewirkt damit eine Kraft. Die elektromagnetische Kraft wird also durch einen Einmischungseffekt, wegen der Ununterscheidbarkeit der inneren Systemkugeln von den äußeren Feldkugeln, hervorgerufen. Die Theorie, also der Beschreibungsformalismus, wird hiermit eichinvariant. Die prinzipielle Verwandtschaft mit den Methoden der allgemeinen Relativitätstheorie wird bei den höheren Eichsymmetrien noch deutlicher.

Der Parameter a(x) kann vermutlich dem Stoßachsenwinkel zugeordnet werden. Die im mathematischen Beweis vorzunehmende Ersetzung durch e lambda(x), wobei e die Elementarladung ist, führt damit zu einer, zu diesen Überlegungen alternativen, Einführung des elektromagnetischen Feldes. Dessen Feldgrößen werden natürlich durch den Vektorwinkel ß und die damit verbundenen Abweichungen von den Normalraum-Erwartungswerten erzeugt.

Auch die Elementarladung selbst kommt so aufgrund ihrer Einheitsdefinition, z.B. im CGS-System, einem modellmäßigen Verständnis näher. Nochmals soll hier betont werden, daß lokal durchaus beliebig große, aber unmeßbare Geschwindigkeitswerte vorkommen können.

Literatur:
[B 86] Bethge, K, Schröder, U.; Elementarteilchen und ihre Wechselwirkungen; Darmstadt 1986
[BH 79] Böhm, H., Hollik, K.; Eichtheorien der starken, elektromagnetischen und schwachen Wechselwirkung; Physik in unserer Zeit, Weinheim 1979

Inhalt Grafik vorheriges nächstes Links

Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)