(Einführung ins Modell der starken Wechselwirkung)
 |
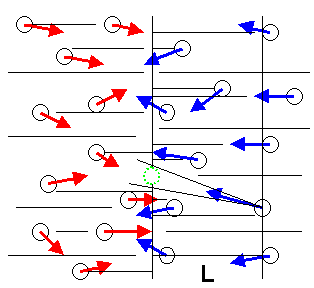
Die starke Wechselwirkung, auch als van der Waals Rest der durch die Quantenchromodynamik (QCD) beschriebenen Wechselwirkungen zwischen den Quarks, ist ausschließlich auf die Stoßwahrscheinlichkeit der Uratome zurückzuführen. Ein Stoß tritt sicher ein, wenn die Relativgeschwindigkeiten im Stoßkegel liegen. Wegen der Unkenntnis aller Orte und Geschwindigkeiten müssen wahrscheinlichkeitstheoretische Methoden verwendet werden. Am einfachsten werden diese durch eine gedankliche Verschiebung von Uratomen in eine dicht gefüllte Ebene verstanden. Alle dazu nötigen Kugeln ergeben die durchschnittliche freie Weglänge L und damit den wahrscheinlichen Aufenthaltsbereich der Stoßzentren (Quarks). |
Globale, im Großen geltende, äußere Symmetrien, wurden vorn beschrieben. Diese können aus nichtabelschen deterministischen lokalen Symmetrien, wie sie bei Einzelstößen (Auftreten der Permutationsgruppe) vorkommen, konstruiert werden. Dabei werden größere Gesamtheiten von Uratomen, also statistische Teilmengen der Grundmenge betrachtet, welche zu abelschen und nichtabelschen Symmetrien auf lokaler und globaler Ebene führen. So folgt, u.a. wegen der Isometrie aller Gruppen zur Permutationsgruppe, das Auftreten der U(1), wo Stoßachsen- und Vektorwinkelerwartungswerte nicht verschoben werden und die Mischung der Urmaterie zur Superponierbarkeit führt. Die SO+(3,1) wird erzeugt, wo in großen Mengen relativ große Geschwindigkeiten untersucht werden. Durch die Betrachtung der räumlichen Drehungen, im Zusammenhang mit der auftretenden SO(3), folgt die Darstellungsmöglichkeit des Spins durch die SU(2).
Auf bekannte Weise führt die geforderte relativistische Invarianz der so zu beschreibenden Materie zur Klein-Gordon-Gleichung oder zur Dirac-Gleichung, je nach dem, ob die Psi-Materie ganzzahligen Spin (0) oder 1/2-zahligen hat.
Bei der Spinor-Materie mit Spin 1/2 tritt noch innere
Selbstwechselwirkung auf. Punktartig wirksame Selbstwechselwirkung des
spinoriellen Materiefeldes wird beispielsweise durch die Heisenbergsche Weltformel
in dem nichtlinearen Glied berücksichtigt (vgl. [H 67] S. 26f).
Ansonsten hat diese den gleichen Aufbau wie die Dirac-Gleichung. Die in
den Zweipunktfunktionen vorkommende Elementarlänge
L
(rund 10-13 cm, nicht zu verwechseln mit der auch in Superstringtheorien
verwendeten Planckschen Elementarlänge von 10-33
cm) entspricht nach diesem Modell der in dem betrachteten System vorkommenden
durchschnittlichen freien Weglänge der Uratome. Vor allem entfallen
aber, wie bei den Stringtheorien, die durch Heisenberg noch nicht vermeidbaren
Singularitäten.
Vorkommenden geometrischen Strukturen in diesen Mengen,
wie z.B. Wirbeln, können die bekannten Quantenzahlen
zugeordnet werden. Dadurch werden von der gesamten Wellenfunktion im allgemeinen
Teile abgespalten, für die bekannte Berechnungsverfahren existieren.
Das nichtlineare Glied in der Heisenbergschen Weltformel ist dagegen schwer
berechenbar. Deshalb ist der andere Weg, statt diesem bestimmte
Eichfelder
einzuführen, welche wiederum quantisierbar sind, erfolgversprechender.
Mathematischen Beschreibungsmöglichkeiten von Materieportionen liegt das Gleichgewichtsverhalten in allen Raumrichtungen gegenüber dem Normalraum zugrunde, was auch als Forminvarianz der betrachteten Größen bezeichnet werden kann. Die bekannten Erhaltungssätze lassen sich damit gemäß der Noether-Theorie (vgl. z.B. in [S 89]) ableiten. Dieses Gleichgewichtsverhalten fordert bei der Einführung gewisser Größen, zur mathematischen Beschreibung der betrachteten Mengen, die gleichzeitige Einführung von Eichfeldern, damit die Forminvarianz gewährleistet wird. Deren für sich betrachtetes Gleichgewichtsverhalten bedeutet Quantisierung und somit die Einführung entsprechender "Teilchen" was hier Urmaterieportionen, also Uratome, sind.
Ein scheinbarer Widerspruch ergibt sich erst durch die experimentelle Erfahrung, daß einer Menge, unabhängig voneinander, zwei oder mehrere Male die gleiche Symmetrie für verschiedene Eigenschaften zugeordnet werden muß. Dabei sind lokale Betrachtungen erforderlich. So kommt man auf natürliche Weise zur Anwendung der infinitesimalen oder Lieschen Theorie. Die Grenze der Superponierbarkeit ergibt sich logischerweise durch die Ausdehnung der Uratome, aus denen ja die betrachteten Mengen bestehen. Das Wesentliche ist jedoch, daß die den Symmetrien zugeordneten Quantenzahlen auf der infinitesimalen Ebene der Betrachtung nicht mehr mischen (Selbstwechselwirkung), was im Auftreten gewisser Kommutator- Beziehungen zum Ausdruck kommt. So können bestimmte Quantenzahlen erhalten bleiben. Mathematisch untersuchbare Strukturen können aber bis ins Unendliche reichen und bringen gleichzeitig eine gewisse Ordnung in die statistische Vielfalt der Uratombewegungen.
So können beispielsweise der Spin und der mit der gleichen Symmetrie SU(2) behaftete Isospin der gleichen Materieportion zugeordnet sein. Das Auftreten des Isospins deutet deshalb auf eine doppelte Verwirbelung in der Menge hin. Diese kann nur durch Konstituenten (Quarks) verursacht sein, welche nicht allein existieren können, weil sich deren Spins sonst additiv verhalten müßten. Geometrisch äquivalent ist die Vorstellung, daß die Ecken eines Dreiecks nicht allein existieren können.
Besondere Bedeutung bei der Systematisierung der vorkommenden Systembildungen erreicht die SU(3) mit ihren Multipletts wahrscheinlich wegen des Auftretens der 8 unabhängigen Parameter. Diese dienen ja auch zur Beschreibung eines elementaren Stoßgebildes (ohne Berücksichtigung der Anzahldichte, ausgedrückt durch d/L). Dabei ist die durch Selbstwechselwirkung (Stöße, Operator T, welcher zuerst das Konjugiertkomplexe bildet und dann mit i multipliziert) erzeugte Unitarität von Bedeutung.
Die gesamten Symmetrien der Quantenmechanik (vgl. z.B. in [GM 90]), bis zu den Winkeln der Wurzelvektoren von Lie-Algebren, lassen somit eine modellmäßige Erklärbarkeit mit Hilfe von Uratombewegungen erhoffen. Das gleiche gilt für die damit ableitbaren Quantenzahlen und mit diesen formulierten Eichfeldtheorien, z.B. der starken und elektroschwachen Wechselwirkung (vgl. [B 81]). Umfassendere Symmetriegruppen, wie die SU(5) des Standardmodells der Elementarteilchen wurden eingeführt, um bewährte Theorien, wie die QED, die vereinigte elektroschwache Wechselwirkungstheorie (WSG-Theorie) und die QCD in einem Modell zu vereinigen (SU(3)c x SU(2)w x U(1)). Daß dazu auch das Konzept der spontanen Symmetriebrechung gehört, zeigt die Kompliziertheit der mathematischen Beschreibung der in der Natur vorkommenden Urmaterieportionen. Verwendete Ideen zur Erklärung der Wechselwirkungen als Raumverzerrungen, Paralleltransport von Vektoren auf Geodäten,... finden sich auch in der allgemeinen Relativitätstheorie wieder. Nur weiterführende Ideen, wie Strings oder hier die einfacheren Uratome bringen aber Ansätze für ein einheitliches Verständnis und die Vermeidung mathematischer Probleme bei den Grenzübergängen gegen Null (Singularitäten).
Zunächst sollen aber anhand der gängigen Modelle etwas eingehender die Systembildungen, also Elementarteilchen und deren so wichtige Stabilität gegenüber ihrer Umgebung, betrachtet werden.
Literatur:
[B 81] Becher, Böhm, Joos; Eichtheorien der starken
und elektroschwachen Wechselwirkung; Stuttgart 1981
[GM 90] Greiner, W., Müller, B.; Quantenmechanik,
Teil 2 Symmetrien; Thun, Frankfurt a.M. 1990
[H 67] Heisenberg, W.; Einführung in die einheitliche
Feldtheorie der Elementarteilchen; Stuttgart 1967
[S 89] Schmutzer, E.; Grundlagen der theoretischen Physik,
mit einem Grundriß der Mathematik für Physiker; 2 Bde Mannheim,
Wien, Zürich 1989
|
|
|
|
|
|