Struktur und Dynamik der Materie im
3
Beschreibung einer Kugelmenge
3.1 Skalare bzw. binäre
Alternativen
Nach der verbalen Beschreibung der Grundmenge
durch das Uratom-Axiom, ist für die
mathematische Darstellung die Existenz des, unserem Anschauungsraum
entsprechenden, dreidimensionalen Ortsraumes anzunehmen. Wegen der Bewegung
unendlich vieler Kugeln existiert darüber hinaus eine eindimensionale
kontinuierliche Parametermenge zur Beschreibung dieses Verhaltens, welche wir
Zeit nennen. Stehen wir dabei auf dem Standpunkt, dass nur die elementaren
Ereignisse, also Stöße, wichtig sind, wäre die Zeit abzählbar. Vielleicht
kommen wir so sogar zu einer Art Quantisierung, was aber hier nicht weiter
verfolgt werden kann.
Im
vierdimensionalen, noch euklidischen, Raum-Zeit-Kontinuum ergibt sich als
elementarste Beschreibungsmöglichkeit des Verhaltens einer sich darin
bewegenden Menge von Kugeln (oder Uratomen bzw. dichten Punktmengen), die
Zuordnung von Uralternativen zu jedem Raum-Zeit-Punkt, entsprechend dem
Vorhandensein von Materie bzw. "Etwas" oder dem Nichtvorhandensein.
Diese Beschreibung könnte als "skalares Feld" im 4-dimensionalen
Vektorraum interpretiert werden. Damit kann nun versucht werden,
Relativitäts- und Quantentheorie sowie die gesamte theoretische Physik
abzuleiten (vgl. Betrachtungen über eine Urtheorie in [W 85]).
Die
Bewegung einer einzelnen Kugel lässt sich durch einen Vektor
![]() R³ darstellen.
R³ darstellen.
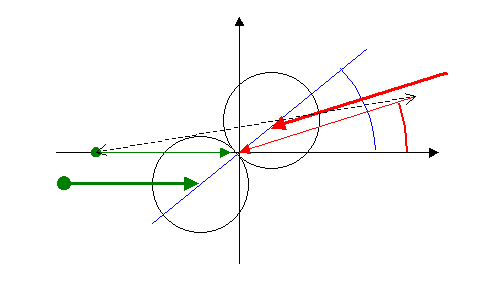
Zu einem Zusammenstoß gehören zwei bewegte
Kugeln (bzw. solche beschreibende Punktmengen), die einander berühren. Die
Stoßachse entspricht der Berührpunkt-Normale (blau). Diese kann in einem
einmal gewählten Koordinatensystem durch einen Einheitsvektor beschrieben
werden. Der Berührungspunkt und damit auch der (eigentlich zweidimensionale)
Stoßachsenwinkel (blau) kann maximal orthogonal zur Relativgeschwindigkeit
(gestrichelt) liegen. Mit gleichem Stoßvektorwinkel (rot) ist deshalb eine
Schar paralleler Flugbahnen aus diesem Bereich möglich.
Es seien (für
umfassendere Definitionen => klicken):
|
|
die zwei Stoßvektoren (grün und rot) und
der Stoßachsenvektor (blau). |
Dann wird
![]()
die zur Stoßachse parallele
Geschwindigkeitskomponente des i-ten Stoßvektors und
![]()
die zur Stoßachse orthogonale
Geschwindigkeitskomponente des i-ten Stoßvektors.
Beim
Zusammenstoß werden die parallelen Geschwindigkeitskomponenten ausgetauscht,
die orthogonalen bleiben auf der jeweiligen Kugel erhalten:
![]()
Das ist die Stoßformel (ausführlicher =>
klicken) des Uratom-Modells.
Der eigentliche Stoß entspricht also nach dem
Uratom-Axiom einer Drehung des Koordinatensystems in die Stoßachsenrichtung
und anschließende Vertauschung (Transposition) der zur Stoßachse parallelen
Komponenten. Dabei wird, unabhängig davon, welches gleichförmig bewegte
Koordinatensystem zugrunde gelegt wird, die Relativgeschwindigkeit an der
zur Stoßachse orthogonalen Ebene (Stoßebene) gespiegelt.
Fürs Verständnis des Uratom-Modells sind die
bis zum Kapitelende vorgestellten Spekulationen
(eines Laien und Autodidakten) nicht von Bedeutung. Wichtig werden sie
möglicherweise bei der Entwicklung einer exakten Theorie. Nachgeschlagen
werden können diese Gedanken unter:
3.3 Beschreibung durch Matrizen bzw. Tensoren
In welcher Form diese Transformationen zur
Beschreibung von Stößen in der zu entwickelnden Theorie sinnvoll ist, muss
noch geklärt werden. Auch die Verwendung komplexer Zahlen könnte eine
mathematische Vereinfachung ermöglichen, ohne dass die etwas an der realen
Existenz der vermuteten Uratome ändern würde. Siehe dafür:
Bereits
aus dem Uratom-Axiom folgt, dass alle Wechselwirkungen auf das Verhalten der
elementaren Kugeln zurückführbar sein müssen. Falls zwei bewegte Kugeln
durch je einen Geschwindigkeitsvektor dargestellt werden, stellt sich die
Frage, wie man am günstigsten, die den beiden Vektoren, kurz vor dem Stoß,
zum Stoßzeitpunkt und kurz danach, zugeordnete Situation, beschreiben kann.
In die beiden bisherigen Stoßformeln gingen zur Beschreibung eines
Geschwindigkeitsvektors nach dem Stoß die Komponenten beider Vektoren ein. Es
bietet sich nun als laienhafte Idee an, die jeweils zwei
Geschwindigkeitsvektoren vor und nach dem Stoß in entsprechenden komplexen
Gebilden zusammenzufassen. In der Raum-Zeit erfolgt dann eine nächste Stufe
der Erweiterung:
Die bisher betrachteten Größen beschreiben die
Eigenschaft der Grundmenge an einem Raum-Zeit-Punkt. Ordnen wir jedem dieser
Punkte eine der vorn beschriebenen Eigenschaften zu, kommen wir auf
natürliche Weise zur Definition von Feldern.
Dabei
verwirrt zunächst das Durcheinander der vorkommenden Geschwindigkeiten und
Winkel. Notgedrungen muss deshalb hier die deterministische Betrachtungsweise
verlassen werden.
Durch die
Zuordnung von Erwartungswerten der skalaren, vektoriellen, tensoriellen und
spinoriellen Größen steht der Apparat der Feldtheorie zur Verfügung.
Immer
sollen darin aber die einfachen Stoßgesetze der kanonischen
Mechanik gelten. Bei der Annäherung zweier Systeme, wenn die inneren, die
Systeme erhaltenden, Eigenschaften stark genug sind, erfolgt die
Selbstwechselwirkung durch den Stoß der einzelnen Kugeln. Wechselwirkungen
können aber auch durch Superposition (Mischung) zustande kommen. Als
Masse-Begriff kann schon hier vorgreifend die Anzahl der beteiligten Kugeln
angenommen werden.
Selbstwechselwirkung
der Feldgrößen durch den Tausch einer Komponente bei einem elementaren
Zusammenstoß spielt bei der üblichen Betrachtung in der Physik bisher keine
Rolle, obwohl gerade durch diese eine ständige Veränderung der Feldgrößen
zu erwarten wäre. Ständige chaotische Änderungen würden aber nach der
gängigen Vorstellung alle weiteren Überlegungen ad absurdum führen. Ohne
diese ist eine modellmäßige Beschreibung und damit das Verständnis der in
den modernen physikalischen Theorien vorkommenden geometrischen Objekte,
welche auf die zusammenstoßenden Uratome zurückführbar sind, möglich. Die
Uratome würden dabei als unendlich klein angenommen. Das ist die notwendige
Bedingung für die Akzeptanz des vorgeschlagenen Weges. Als hinreichende
Bedingung werden nun Vorgänge in der Grundmenge mit Selbstwechselwirkung
untersucht, weil landläufig angenommen wird, dass in einer Menge wirr
durcheinander fliegender stoßender Kugeln keine stabilen Systeme entstehen
können.
Im
derzeitigen Entwicklungsstadium des Uratom-Modells werden nur reelle Vektor-
Größen verwendet.
Literatur:
[F 89] Fachlexikon ABC Physik; 2
Bde; Thun, Frankfurt/M, 1989
[S 89] Schmutzer, E.; Grundlagen
der theoretischen Physik, mit einem Grundriß der Mathematik für Physiker; 2
Bde Mannheim, Wien, Zürich 1989
[W 85] von Weizsäcker, C.F.;
Aufbau der Physik; München, Wien 1985
Stichworte (Ende)
![]()
Wiese, Lothar: Struktur und Dynamik
der Materie im Uratom-Modell, http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)