Struktur und Dynamik der Materie im
Uratom-Modell
5.3 Leptonen
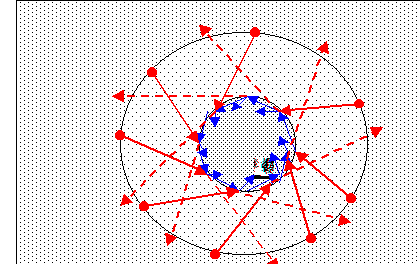 |
Lepton, gemäß
Definition als Elektron zu interpretieren.
Der innere dichte (eigentlich über den Rand verschwommene
dunkelgraue) System-Stoßbereich mit kleinen Geschwindigkeiten kann,
durch die maximal erreichbare Zusammendrängung, eine gewisse Grenze
nicht überschreiten. Dessen Stabilität in Form einer Solitonen
ähnlichen Welle wird durch den Systembildungprozeß
erreicht. Zur Gesamtenergie trägt auch das Feld bei, welches den äußeren
Stoßbereich mit Normalraum-Uratomen bildet. |
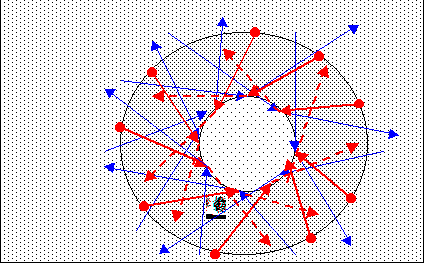 |
Anti-Lepton, gemäß
Definition als Positron zu interpretieren.
Der ringförmige dichtere Bereich wird durch Uratome
mit hoher Geschwindigkeit aufgespannt. Die blauen Vektoren verlassen das
System nicht. Dessen Stabilität in Form einer Solitonen ähnlichen
Welle wird durch den Antisystembildungprozeß
erreicht. Zur Gesamtenergie trägt auch das Feld bei, welches hier
von den kürzeren roten Geschwindigkeitsvektoren gebildet und teilweise
in den dichten grauen (eigentlich verschmierten) System-Uratom-Stoßbereich
hineingezogen wird. |
In den Elektronen- bzw. Positronenladungen vermuten
wir die einfachsten Quellen des elektromagnetischen Feldes. Eine Uratom-Menge,
welche hier vorerst vereinfacht als ein dichter Wirbel in einer sehr dünnen
Umgebung angenommen wird, verändert bei kontinuierlicher Beschleunigung
weder den Spin noch die Ladung. Maximale Geschwindigkeit ist aller Erfahrung
nach die Lichtgeschwindigkeit. Deshalb wird zur Beschreibung die Lösung
der freien Dirac-Gleichung in Form ebener Wellen herangezogen. Am verbreitetsten
ist der Formalismus von Bjorken und Drell ([BD M und F]. Hier wurde aber
eher zufällig die Darstellung von Greiner und Schröder verwendet
(vgl. [GS 89], S.33f). Mit positiver Energie und positivem Impuls ist das
Psi ~ e(-ip-x),
mit p = (E,pvect ).
Damit ergibt sich für das Elektron (mit sigma
als Vektor der zweidimensionalen Pauli-Matrizen) ein Viererspinor:
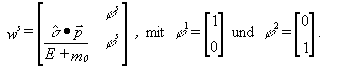
(vgl. [GS 89] S35) als Lösung der freien Diracgleichung
für Spin auf bzw. Spin ab.
Entsprechend wird bei negativer Energie und negativem
Impuls
Psi ~ e(ip-x) = e(-i(-p)-x)
= e(p´-x), mit p´=
(-E,-pvect )
und als Viererspinor für das Positron ergibt sich:
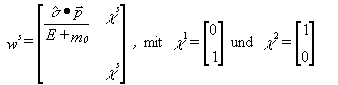 .
.
Das Auftreten des Spin 1/2, welcher sonst nur mathematisch
erschlossen wird, läßt sich jetzt verstehen. Im Gegensatz zu
den Eichbosonen bzw. Photonen mit dem Spin 1 tritt nämlich wegen der
Ortsstabilität zum ersten Mal ein lokalisierbares systeminneres Stoßzentrum
auf. Dieses kann sich über das ganze, durch die freien Weglängen
aufgespannte, Gebiet bewegen. In Streuversuchen erscheint es aber punktförmig.
Jeweils sind zwei Stoßpartner beteiligt, welche zum Großteil
aus dem Normalraum mit Durchschnittsgeschwindigkeit kommen. In der Sprache
der Chaosforscher kann man das Stoßzentrum als nahezu punktförmigen
Attraktor bezeichnen. Annäherungs- bzw. Entfernungsgeschwindigkeitsbeträge
bleiben bei den Stößen konstant, die Richtungen werden aber,
wegen der durchschnittlichen Stoßachsenwinkel von 45°, um 90°
gedreht. Deshalb muß, wie gezeigt, entsprechend der Drehung einer
festen Kugel, in Streuversuchen der Spin 1/2 gemessen werden. Die Systemdrehung
erfolgt orthogonal zur Bewegungsrichtung und ist deshalb auch geschwindigkeitsunabhängig.
Bei der Bewegung vom Stoßzentrum weg, treffen
die Uratome nach durchschnittlich einer freien Weglänge auf ein Uratom
des Normalraums. Die Dichte hat dort schon so stark abgenommen, daß
fast nur noch Frontalstöße auftreten. Der Weiterflug der Normalraumkugel
nach innen ist deshalb nur durch den Stoßachsenwinkel gedreht.
Wegen der großen Dichte im Stoßzentrum
und den dort stark verkürzten freien Weglängen, welche nicht
identisch mit der Compton-Wellenlänge, d.h. der durchschnittlichen
freien Weglänge des gesamten Systembereichs sind, kommen im Systeminneren
viele Querstöße vor. Dadurch wird i.A. gemäß Stoßformel
auf den beiden Stoßpartnern ein unterschiedlicher Geschwindigkeitsbetrag
erzeugt. Mindestens ein Stoßpartner besitzt vor dem Stoß mit
hoher Wahrscheinlichkeit die Normalraum-Durchschnittsgeschwindigkeit, während
der andere ein systeminnerer sein kann. Sind die kleineren Geschwindigkeitsvektoren
nach dem Stoß die systeminneren, verlassen die größeren,
als ladungsbildende Vektoren, das System und umgekehrt (positive
bzw. negative Ladung). Wegen der natürlichen Vektorwinkel-
und Stoßachsenwinkel-Streuung, kommen immer auch störende Vektoren
vor. Deshalb müssen für den Masse-, Spin- und Ladungserhalt durch
den Systemerhaltungseffekt zum Ausgleich der Randfluktuation genügend
systemerhaltende Vektoren erzeugt werden. Das sind in der Gesamtbilanz
alle, die wegen ihrer Eigenschaft ins System passen.
Die drei durch ihre Massen unterschiedenen Leptonengruppen
können anschaulich erklärt werden, weil bei der kontinuierlichen
Dichtezunahme der betrachteten Uratom-Menge die freie Weglänge entsprechend
abnimmt. Beim ersten Auftreten eines stabilen Systems in der wirbelnden
Menge ist erstmals der solitonbildende Systembildungseffekt, wie beschrieben,
erreicht. Die auftretenden Querstöße, welche von den gleich
großen Normalraum-Uratomen dominiert werden, sind demnach die ersten
ihrer Art, also primäre Querstöße. Zugeordnet wird
das Leptonenpaar e±.
Bei der Kombination eines bestimmten Vektorwinkelerwartungswertes,
mit einem Stoßachsenwinkel- und einem Geschwindigkeitsbetrags-Erwartungswert
der zum System gehörenden Kugel, unter der Annahme des Zusammentreffens
mit einer Normalraumkugel, ergibt sich ein fester Erwartungswert der erwarteten
Bahnen nach dem Stoß. Jede der beiden beteiligten Kugeln kann mit
gleicher Berechtigung weiter zum System gehören. Die Auswahl der Zugehörigkeit
erfolgt automatisch durch den Weg und die Entscheidung, ob die Kugel eine
ins System passende Eigenschaft besitzt. Bei Antisystemen ist dabei nur
die Geschwindigkeitsbetragsdifferenz entgegengesetzt. Ist jedoch im Durchschnitt
bei den immer um den Erwartungswert gestreuten Winkeln, eine stärkere
vom System weg gerichtete Bewegung zu erwarten, als durch den Systembildungseffekt
nachgeliefert wird, löst sich das System schnell auf. Eine gegen
unendlich gehende Lebensdauer wird so, unter der Voraussetzung, daß
nur ein systeminneres Stoßzentrum in Frage kommt, nur bei einer
Dichte und damit einem Stoßvektorwinkel-Erwartungswert
erreicht. Die "Erwartungswerte-Bahn" könnte dabei ein gleichseitiges
Dreieck (60° Innenwinkel) sein, was aber erst in der vorgeschlagenen
Theorie genau zu untersuchen ist.
Weitere Dichtesteigerung erhöht die Anzahl der
Querstöße und die freie Weglänge sinkt weiter. Dabei verschiebt
sich auch der Erwartungswert des Vektorwinkels. Beim Stoßachsenwinkel
gilt aber weiterhin die Symmetrie des gleichen Ergebnisses bei positiven
oder negativen Winkeln und des unveränderten Erwartungswertes wegen
parallel gleich wahrscheinlicher Bahnen, welche den für die Stabilität
zur Umgebung wichtigen festen Spin erzeugen.
Ein zweites Maximum im Massenspektrum bei gewissen
Versuchen, das nicht allein von relativistischer Energie herrührt,
muß nun zum einen mit einem größeren Vektorwinkel und
zum anderen mit einer kürzeren systeminneren freien Weglänge
verbunden sein. Die "Erwartungswerte-Bahn" könnte dann z.B. ein Quadrat
(90° Innenwinkel) sein. Eine Verbindung dieses Gedankenganges mit den
in Lie-Algebren vorkommenden Winkeln der Wurzelvektoren ist denkbar. In
dem, immer noch einzelnen, Stoßzentrum sind aber sicher wegen der
höheren Dichte auch systeminnere, also sekundäre Zusammenstöße
der Systemkugeln untereinander zu erwarten, bevor diese wieder mit einem
Normalraum-Uratom zusammentreffen. Diesen Maxima wird die zweite Leptonengruppe
µ± zugeordnet.
Ähnliche Überlegungen mit tertiären
Zusammenstößen führen zur dritten Gruppe, bei
den Leptonen also t± (beispielsweise als Fünfeck
mit Innenwinkel 105° oder Sechseck mit Innenwinkel 120°).
Zugehörige Neutrinos
werden meist durch die Weyl-Gleichung beschrieben. Ihr Modell entspricht
der Paulischen Vorstellung zur Erklärung der Restenergie.
Im Stoßzentrum gibt es keine Stoßvektorwinkel-Erwartungswert-Verschiebung.
Nur die Stoßachsen sind entsprechend der Relativgeschwindigkeitsrichtung
natürlich gestreut. Wegen der wiederum geltenden ±- Symmetrie
kann der sich ergebende Spin 1/2 gemäß der Erzeugung das vorerst
einzige Erscheinungsmerkmal sein. Er kann in oder gegen die Bewegungsrichtung
eingestellt sein und wird dem entsprechenden Neutrino bzw. Antineutrino
zugeordnet. Deshalb ergibt sich die beobachtbare Chiralität
(Rechts- bzw. Linkshändigkeit) bzw. Helizität. Das Auftreten
primärer, sekundärer und tertiärer systeminnerer Stöße,
welchem nue,
numu
und nutau
zugeordnet wird, ist wegen des schnellen Davoneilens, mit der h
- abhängigen freien Weglänge verbunden. Deshalb entsteht lokal
unter gewissen Voraussetzungen nicht die für Querstöße
erforderliche Dichte.
Stoßzentren sind mit den Symmetriezentren der
Rotationsgruppe (SU(2)) zu identifizieren. Die Ordnung aller Leptonen ergibt
sich durch die zulässigen Multipletts. Bei j = 1/2 ergibt sich ein
Dublett in jeder durch die Dichte bestimmten Weglängen- bzw. Vektorwinkel-Hierarchieebene
(Flavour e, µ, tau ). Eine absolute Begrenzung der Stufenzahl ist
durch die Raumauffüllung gegeben.
Literatur:
[BD-M 90] Bjorken, J.D., Drell, S.D.; Relativistische
Quantenmechanik; BI Mannheim, Wien, Zürich 1990
[BD-F 90] Bjorken, J.D., Drell, S.D.; Relativistische
Quantenfeldtheorie; BI Mannheim, Wien, Zürich 1990
[GS 89] Greiner, W., Schäfer, A.; Quantenchromodynamik;
Thun, Frankfurt a.M. 1989
Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell,
http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)


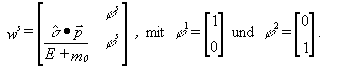
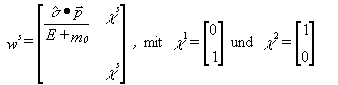 .
.