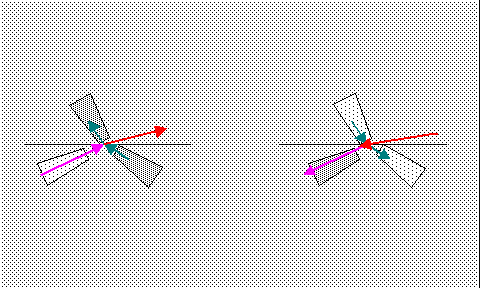
Das Auftreten weiterer Stoßzentren wird durch die Verkopplungen der Drehimpulsalgebra beschrieben. Jedes Stoßzentrum wird dabei betrachtet als im Gleichgewicht befindlich mit dem umliegenden Normalraum.

Eine natürliche Erweiterung dieses Gedankenganges führt zum Vorkommen systeminnerer Stoßzentren, welche sich im lokalen Gleichgewicht mit dem umliegenden Raum, aber insgesamt in einen Wirbel eingeschlossen finden, der sich im Gleichgewicht mit dem Normalraum befindet. Damit ist die Dominanz zusammenstoßender Normalraumvektoren schon auf der ersten Hierarchieebene, mit primären Querstößen, aufgehoben.
Zwischen den zwei, drei oder mehr auftretenden Stoßzentren müssen deshalb die Stabilität aufrecht erhaltende und gleichzeitig die Gesamtanzahl der am System beteiligten Uratome (Masse) erhöhende Uratomflüsse stattfinden. Das Gleichgewicht, durch die gesamte Systemoberfläche ein- und ausfließender Uratome, erlaubt ja durchaus höhere Flüsse innerhalb.

Quarks, hier z.B. das "up" mit seinem Antiteilchen, sind gekennzeichnet durch den Einschluß in Elementarteilchen (confinement). Unterschied zum Lepton ist, daß systeminnere Uratom-Flüsse kein eigenes Stoßgleichgewicht zum Normalraum entwickeln müssen, weil die Ströme teilweise vom anderen Quark geliefert werden. Daher wird eine größere Dichte und kleinere interne freie Weglänge möglich. Diese bestimmt den Aufenthaltsbereich der Uratom-Ströme und damit das "confinement".

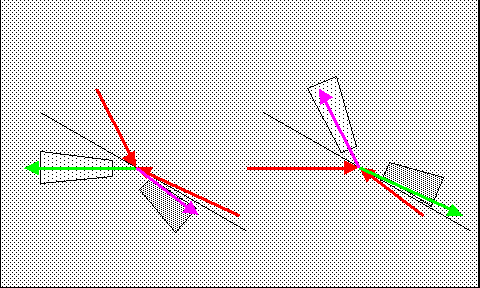
Beim "down" können beispielsweise auch je zwei äußere und innere Uratom-Flüsse auftreten, wodurch in Elementarteilchen gerade die beobachteten Kombinationen ermöglicht werden. Die Graustufen sollen wie oben zugehörige Anzahldichten darstellen. Zulässige Geschwindigkeiten und Dichten ergeben sich in Übereinstimmung mit dem Standardmodell aus der Theorie. Wesentlich ist auf jeden Fall, daß auch Quarks durch die elementaren Stoßgebilde erzeugt werden, jedoch nicht allein existieren können.

Der zwischen den, in der Größenordnung von L nahe beieinander liegenden Stoßzentren, immer eingeschlossene Raum bietet nun Aufnahme für weitere Uratome, falls diese sich in Richtung der Stoßzentren bewegen. Deren Dichte muß in der Größenordnung liegen, die durch die freien Weglängen der Stoßzentren diktiert wird. So erweitert sich deren an und für sich stark begrenzter Bereich enorm. Das läßt eine viel größere Masse des Gesamtsystems zu.
Der "Kometenschweif" der Stoßzentren aus Geschwindigkeitsvektoren, welche kleiner oder größer als die Normalraumvektoren sein können, verhindert deren selbständigen normalen, mit dem Vakuum im Gleichgewicht befindlichen Spin. Es wird ein Isospin erforderlich.
Statistisch vermischen sich allerdings die Stoßzentren und Uratomflüsse zwischen diesen im System. Die Auffüllung des Zwischenbereichs erfolgt natürlich durch den Systembildungseffekt, d.h. durch den Dichtezuwachs bis zur maximalen Grenze, welcher durch die in noch größerer Zahl als bei den Leptonen auftretenden Querstöße verursacht wird.
Wegen der großen Massen und kleinen freien Weglängen sich im Systeminnern kreuzender Uratomflüsse, kann die Systemoberfläche kleiner als bei vergleichbaren Leptonen sein. Die Randfluktuation wird deshalb kleiner, was die Stabilität erhöht. Andererseits kann, durch sich systemintern kreuzende Ströme, neue Instabilität entstehen.

Wegen des Wirbelcharakters der Stoßzentren ist jeweils eine Beschreibung mit zu SU(2) isomorphen Multipletts erforderlich. Diese werden als T-, U- und V- Multipletts, welche Unteralgebren der SU(3) sind, bezeichnet. Die SU(3) ist ja besonders wegen der beobachteten Ordnung der Hadronen ausgezeichnet. Sie besitzt neben den 8 Generatoren 8 freie Parameter, die den unabhängigen Größen der allgemeinsten elementaren Stöße zugeordnet werden können.

Die neu eingeführten Stoßzentren, welche große Ähnlichkeit mit den Leptonen haben, können nicht allein im Normalraum existieren. Sie weisen alle Merkmale auf, wie sie die durch Gell-Mann als Quark bezeichneten und mit Hilfe der T-, U- und V-Algebren beschriebenen psi - Materie- Portionen besitzen (vgl. z.B. [GM 90], S. 260). Für die systeminnere Stabilität der Quarks ist eine Umgebung erforderlich, welche nicht dem Vakuumserwartungswert des Normalraums entspricht. Die systemerhaltenden erwarteten Stöße können nur von einer naheliegenden "Ecke", also einem anderen Quark, kommen. Dadurch bedingt sich deren gegenseitige Existenz.

Ob der große oder kleine Geschwindigkeitsvektorfluß das Teilsystem bildet, es sich also um ein Quark bzw. Antiquark handelt, wird mit durch den zugehörigen "Kometenschweif" bestimmt. Da die freien Weglängen geschwindigkeitsunabhängig sind, ist wie bei allen Elementarteilchen, die Masse der Antiteilchen gleich. Die im Schattenbereich des "Kometenschweifs", ansammelbare Uratomzahl ist deshalb ebenfalls identisch. Der "Kometenschweif" hat die Funktion eines Leimteilchens und kann deshalb als Gluon bezeichnet werden.

Der Quarkeinschluß bzw. das durch die Quantenchromodynamik geforderte Confinement erfordert wegen der durch die Normalraumeigenschaft h hervorgerufenen freien Weglängen keine selbständigen Kräfte. Das ist das eigentlich Neue am Uratommodell.
Die in den gängigsten Potentialmodellen (vgl. z.B. in [L 89]) verwendeten gleitenden Kopplungskonstanten der Form (siehe [GS 89], S. 275)

lassen aufgrund des vorkommenden Faktors, der eine logarithmische Abhängigkeit vom Kehrwert einer sehr kleinen Zahl wie der Elementarlänge enthält, eine auch quantitative Lösbarkeit des Confinement-Problems erwarten. Ob das aber überhaupt erforderlich ist, muß noch geklärt werden, weil ja bisher keine freien Quarks gefunden wurden.

Eine Beschreibbarkeit durch Gitter-Eichtheorien ist anzunehmen, wobei die Gitterkonstanten durch die freien Weglängen ersetzt werden können.
Die in weiten Bereichen anwendbare Stromalgebra erhält ebenfalls ihre Anschaulichkeit.

Mesonen sind wie nach dem Standardmodell Kombinationen von Quark und Antiquark. Bei den Baryonen werden drei Quarks bzw. Antiquarks miteinander kombiniert. Natürlich muß die Materie zwischen den Stoßzentren statistisch verschmiert sein.
Die verschiedenen Quarkflavour werden durch die im Hadron vorkommenden inneren Uratomströme hervorgerufen. Sie verursachen gemäß der SU(3) - Multiplettbildung vor allem verschiedene Anzahldichten in den einzelnen kombinierbaren Stoßzentren, welche sich auf die Gesamtmasse des Hadrons auswirken. Gleichzeitig entstehen auch Spin, Ladung und magnetisches Moment gegenüber dem umgebenden Normalraum, denen gemäß der üblichen Definition nun anschauliche Uratomströme zugeordnet werden.

Auch für die weiteren Quantenzahlen bieten sich anschauliche Zuordnungen an, der Baryonenzahl beispielsweise die Eigenschaft, aus drei Quarks mit zugehörigen Gluonen, zusammengesetzt zu sein. Die Eigenschaft "Farbe" könnte mit den im Hadron vorkommenden Richtungen der Urmaterieströme verbunden werden, weil ja in den Systemen nach außen alle Richtungen sich wieder zu "weiß" überlagern. So wird auch die Flavour-Blindheit der Farbe und damit der starken Wechselwirkung offensichtlich.

Die Uratomflüsse der Hadronen lassen sich wie die der Leptonen quantisieren. Es müssen nach den bisher bekannten Unterscheidungsmerkmalen also Quarks in mindestens drei Gruppen auftreten, welche von primären, sekundären und tertiären auftretenden Querstößen, mit entsprechender freier Weglänge L, herrühren. Als weiteres Unterscheidungsmerkmal kommt nur die vorn eingeführte Isospinquantenzahl, also auf und ab in Frage. Durch die internen Materieströme wird nun bei den Quarks, welche den Neutrinos entsprechen, eine lokale Stabilität erzeugt, so daß die "Restenergien" nicht mit Lichtgeschwindigkeit davoneilen müssen. Deshalb ergeben sich die bekannten Lepton - Quark- Familien (siehe z.B. in [F 92]):

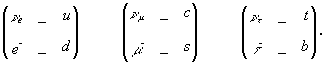
Die explizite Ermittlung der Massen,... ist wegen der noch fehlenden Uratomgröße Aufgabe der angeregten Theorie.

Hiermit ist nun das gesamte Elementarteilchenspektrum im Rahmen der durch das Standardmodell gegebenen mathematischen Beschreibung modellmäßig auf Uratommengen zurückführbar. Einige wesentliche Eigenschaften werden aber erst im Rahmen der quantitativen Untersuchung der Wechselwirkungen deutlich. Die Zusammensetzung der Hadronen aus Quarks wird bereits seit 1961 (Murray Gell-Mann)  durch die Symmetrie des "Achtfachen Weges" beschrieben (vgl. z.B. Die "Geburt" der Quarks).

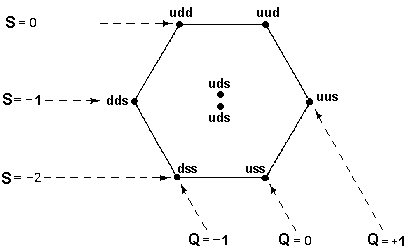
Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace.de, Porec 2000
Uratom (Anfang)