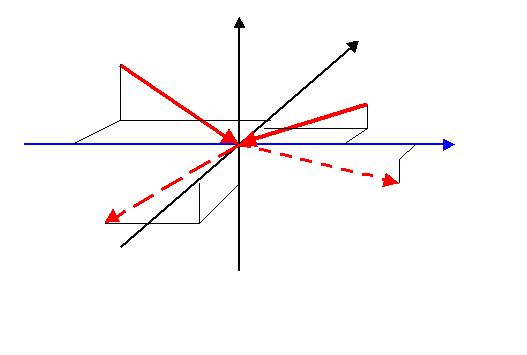
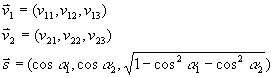
Das ist die Stoßformel des Uratom-Modells.==> Stoßwahrscheinlichkeitsveränderung = lokale Raumzeit-Verzerrung
6 Wechselwirkungen im Uratom-Modell
Einzige direkte Wechselwirkung ist nach dem Uratommodell selbstverständlich der durch die Stoßgleichung ( in Kugelmengenbeschreibung ) beschriebene direkte Zusammenstoß der Uratome. Die Stoßgleichung mit ihrem nichtinfinitesimalen Geschwindigkeitstausch geht deshalb als Grundformel in alle Theorien ein. Wechselwirkungen müssen daher auf diese elementaren Stöße und die einfache Superposition der Uratommengen in der Raumzeit zurückführbar sein. Grenzen beobachtbarer Werte ergeben sich durch die Uratomausdehnung.
 |
Bei Stößen werden nur die Geschwindigkeiten
parallel zur Stoßachse (blau) ausgetauscht.
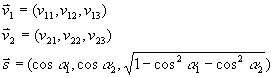
Das ist die Stoßformel des Uratom-Modells.==> Stoßwahrscheinlichkeitsveränderung = lokale Raumzeit-Verzerrung |
Gleiches gilt für den Zwang des Normalraumes,
daß jedes System die durch h und c bestimmte Wellenlänge, wie
in 4.3 beschrieben,
erhält. Auch das ist eine elementare Wechselwirkung.
Trägheit und relativistischer Massenzuwachs sind,
wie in 4.4 gezeigt,
auf die durchschnittliche Uratombewegung des Normalraumes zurückzuführen.
Wesentliche Abweichungen von der Normalraumverteilung der Stoßachsenwinkel müssen im Rahmen der zu entwickelnden Theorie untersucht werden. Ansammlungen von Uratom-Systemen beeinflussen sich durch die elementaren Zusammenstöße mit den Normalraumkugeln natürlich gegenseitig. Das erklärt die Drehbewegungen kosmischer Elementarteilchenansammlungen bis zu den Galaxien. Aber auch im Zwischenvakuum muß durch diese Materieansammlungen und die Selbstwechselwirkung der Felder eine Art Stoßrhythmus hervorgerufen werden, welcher Einfluß auf die Chiralität hat. Von einer gemeinsamen Quelle synchron erzeugte Uratom-Systeme müssen auch an weit entfernten Orten so einen Rest dieser Synchronisation mit sich tragen, was zur Nichtlokalität in vielen Versuchen führt.
Streuversuche von Elementarteilchen nutzen bei hohen Energien vor allem die Wechselwirkung durch direkte Zusammenstöße der beteiligten Uratome. So wird die teilweise Durchlässigkeit der anderen Wechselwirkungen bei hohen Energien verständlich. Der gegenseitigen Beeinflussung von Systemen bei geringen Energien sind, vor allem wegen der Quantisierbarkeit der auftretenden Uratomflüsse, eigene Namen gegeben worden.
Wechselwirkungsstärken oder Kräfte
sind durch das Produkt aus Masse mal Bewegungsänderung definiert.
Nach dem vorn gemachten Ansatz, welcher der Grundüberlegung von Eichtheorien
entspricht, ist damit eine "uratomare" Aufsammlung oder Abgabe von Geschwindigkeitsvektoren
verbunden. Dazu wurde auch schon der Begriff einer Raumverzerrung
verwendet. Hier muß nun bei konsequenter Anwendung des Modells für
die bekannten Wechselwirkungen, der Einsteinschen Wunschvorstellung nach
einer Erklärung von Materiekonzentrationen durch das metrische Feld
nahekommend, nach den wesentlichen Einflüssen von Uratomeigenschaften
auf diese Wechselwirkungen gesucht werden. Aus diesen Konzentrationen,
Winkeln und Geschwindigkeiten sollte dann über die bekannten Wechselwirkungsstärken
auf die Größe und Masse eines einzelnen Uratoms geschlossen
werden können.
|
|
|
|
|
|