Zu quantitativer Beschreibung und modellmäßigem Verständnis der elektromagnetischen Wechselwirkung wurde vorn schon die Anwendbarkeit der U(1)- Symmetrie, wo bei festem ß mit Hilfe von alpha Geschwindigkeitsvektorlängen und damit Uratomströme verändert werden, hergeleitet. Auch die QED sowie die vereinigte Theorie von schwacher und elektromagnetischer Wechselwirkung, also die Weinberg-Salam-Glashow-Theorie (vgl. [B 81] S. 346ff) werden durch die Uratomströme anschaulich. Wesentlich ist die Superponierbarkeit, d.h. der Urmateriemischungen mit der daraus folgenden Schwerpunktsbewegung. In der Mischung können ja eigene nicht von systemfremden Uratomen unterschieden werden. Den Geschwindigkeitskomponenten sind dabei nach der naiven vorn getroffenen Definition die ladungsartigen Komponenten und den Uratom-Anzahldichte-Strömen die magnetischen Feldkomponenten der elektromagnetischen Wechselwirkungen zugeordnet. Wegen der vorgesehenen Einbeziehung der Gravitation in die geplante große Vereinigung des Wechselwirkungsmodells, wird nun deutlich, daß die lokalen Veränderungen von Geschwindigkeiten sowie Anzahldichteflüssen, welche durch die Felder A bzw. V beschrieben werden, durch einfache Einmischung ins System passender Uratome erfolgt. Diese können durchaus auch massiv sein, wie bei einigen Eichbosonen. Beim Feld V ist die Verwirbelung auf einen Stoßachsenwinkel zurückzuführen. A bzw. V sind an eine lokale, mit Spin verknüpfte, also drehende Quelle gebunden. Sie können aber an beliebige (longitudinale) Massen koppeln. Deshalb "fallen" geladene Teilchen ungleich schnell im elektromagnetischen Feld. Kopplung bedeutet hier und überall im Uratom-Modell natürlich nur eine mathematische Zuordnung zusätzlicher im Modell zu betrachtender Größen zu den ursprünglichen Teilmengen aus der Grundmenge. Massen sind ja nur die Anzahlen der beteiligten Uratome.

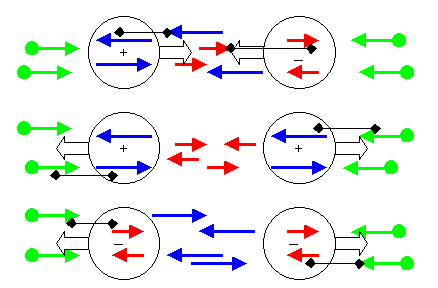
Die elektroschwache Wechselwirkung ist hier in der Form von mischenden Geschwindigkeitsvektoren dargestellt. Obwohl diese eigentlich nur reine elektrische Felder (virtuelle Photonen) beschreiben, kann der Mechanismus auch auf die Uratom-Flüsse (Anzahldichte) des magnetischen Feldes und beispielsweise systeminterne Axialvektorströme der schwachen Wechselwirkung angewandt werden. Allen diesen superponierbaren Wechselwirkungen ist im Uratom-Modell gemeinsam, daß ja die aus anderen Systemen kommenden Uratome nicht von systeminternen unterschieden werden können. Eine Verlagerung des Systemes erfolgt immer dorthin, wo die zu den systeminneren Eigenschaften ähnlichste Umgebung erwartet wird. Das ist hier durch die schwarzen Verbindungslinien angedeutet.

Bei geladenen Systemen haben i.a. die inneren Vektorströme im Durchschnitt einen entsprechend kleineren Geschwindigkeitsbetrag als die nach außen emittierten und umgekehrt. Gleichnamige Ladungen haben somit zwischen sich nicht ins System passende Geschwindigkeitsvektoren. Gelangen diese ins System, ergibt sich bei der Mischung nach außen eine Beschleunigung (Abstoßung). Der Normalraum bietet für die Systeme die günstigeren Erhaltungsmöglichkeiten. Ungleichnamige Ladungen haben im Zwischenraum, vom anderen System geliefert, dagegen Geschwindigkeitsvektoren, wie sie im Innern vorkommen. Deshalb ergibt sich die Anziehung.
Bei den durch die Rotation rot beschriebenen magnetischen Feldern ergibt sich wegen der Dichteveränderungen eine lokale Auftreffwahrscheinlichkeitsveränderung. Diese verursacht in kleinen Bereichen wie das reine elektrische Feld in gewissen Richtungen günstigeres Stoßverhalten und in anderen ungünstigeres. So erhalten die Systemschwerpunkte ihre resultierende Beschleunigung.

Experimentell gesichert ist die relative Stärke im Vergleich zu den direkten Stößen der starken Wechselwirkung von 1/137 oder exakter 0,0072973506 ± 0,000000006. In Streuversuchen sollten gleich geladene Teilchen deshalb eine Geschwindigkeit v > c / 137 haben, bevor es zur direkten Streuung kommt, was experimentell überprüfbar ist. Bei ungleichnamig geladenen Systemen kommt es zur Streuung unter kurzfristiger zusätzlicher Beschleunigung. Handelt es sich um gleichartige Systeme, findet jedes Uratom einen Stoßpartner. Es erfolgt die bekannte Paarvernichtung. Im häufigeren Fall unterschiedlicher Systeme, vor allem aus den beiden Teilchenfamilien der Hadronen bzw. Leptonen, wird in den meisten Fällen die lokale Störung beim Systemzusammenstoß durch den stärkeren internen Systembildungseffekt der Elementarteilchen dominiert. Nach den kurzzeitigen Stoßveränderungen gehen deshalb meist die Elementarteilchen unverändert aus der Streuung hervor. Die U(1)- Symmetrie wird hierbei nicht gebrochen. Welche Ursache hat nun aber das Stärkeverhältnis von 1 / 137  (Feinstrukturkonstante)?

Hier in diesem Modell bietet sich dazu einfach der Gedanke an, daß das auch im Vakuum, oder besser im Normalraum, beobachtbare Stärkeverhältnis, direkt einer positiven oder negativen Geschwindigkeitsabweichung zuzuordnen ist.
Mit der Stoßachsenformel und den Stoßformeln (Geschwindigkeitstausch in Richtung der Stoßachse) ergibt der von den Systemen an der Normalraumgrenze durchschnittlich erzeugte Geschwindigkeitsunterschied von 1 / 137 die Möglichkeit, zugehörige Vektor- und Stoßachsenwinkel zu untersuchen. Im Normalraum des Vakuums sollte sich bei diesen frei durcheilenden Störungen, also Photonen, der gleiche Geschwindigkeits-Unterschieds-Erwartungswert feststellen lassen. Mit diesem kann dann auf den zugehörigen Vektorwinkelerwartungswert geschlossen werden.

Bei Variation von <ß> ist eine Veränderung der Werte von f(<ß>) normal. Die gleichzeitige Änderung der alpha- Werte ergibt ja unterschiedliche erwartete Geschwindigkeitsänderungen, wie in 4.2, auch grafisch, gezeigt. Daraus muß sich nun ein Durchschnittswert des zuordenbaren festen Vektorwinkelerwartungswertes ermitteln lassen, bei dem genau die Geschwindigkeitsunterschiede wie in der elektromagnetischen bzw. schwachen Wechselwirkung erfordrlich ist. Dieser dürfte viel kleiner als der für die starke Wechselwirkung sein. Ob darin direkt 1/137 auftreten wird, müssen die weiteren Untersuchungen ergeben.
 

In der Erwartungswert-Funktion in Abhängigkeit von der freien Weglänge treten Funktionen in den Integrationsgrenzen auf, so daß sich diese z.Z. höchstens numerisch lösen läßt. Hieraus läßt sich direkt auf L im Vakuum, d.h. auf die Vakuumdichte d /L schließen, was aber hier nicht weiter erörtert werden kann.
Stillschweigend vorausgesetzt worden war vorn ein Gleichgewicht zwischen systeminternen und aus dem Vakuum stammenden Uratom-Strömen. Nur bei den Leptonen existiert das wirklich. In Hadronen kommen jedoch Ströme vor, welche nicht selbständig existieren können (Quarks). Zugeordnet werden können diesen, wie vorn erwähnt, Vektor- und Axialvektorstrom- Komponenten in abgewandelter "Iso-Form" mit kurzer Reichweite. Eingeschlossen wird in diesem Modell deshalb die schwache Wechselwirkung. Diese verlangt nur ein Potential vom Coulombschen Typ (vgl. z.B. [B 86] S. 193ff und besonders S.270f). Folge ist eine SU_i(2)xU_y(1)- Eichtheorie der elektroschwachen Wechselwirkung, wie sie durch die damit formal anwendbare WSG-Theorie gegeben ist. Dem SU(2)- Anteil entsprechen die Transformationen wegen des vorkommenden Vektorwinkels ß und dem U(1)- Anteil die Streuung des Stoßachsenwinkels a . Im Gegensatz zur starken Wechselwirkung interessiert hier aber nicht der häufiger vorkommende systembildende, sondern der systemauflösende Bereich der vorkommenden Vektorwinkel in der Systembildungsformel, aus dem die Stärke der Wechselwirkung, nach der Erfahrung in der Größenordnung von 1 / 137, folgt.

Bei zusammengesetzten Systemen ist nach außen ebenfalls Stabilität in allen Richtungen erforderlich, d.h.

Für die Ermittlung der Größenordnung des Kopplungsfaktors der schwachen Wechselwirkung ist die Betrachtung von Streuungen der massiven Eichbosonen W^± und Z⁰ sowie der Neutrinos erforderlich. Beide wirken im Normalfall eher zerstörerisch als systembildend. Axialvektorielle Ströme sind beim erneuten Zusammentreffen mit systeminternen Strömen lokal natürlich nicht von vektoriellen zu unterscheiden. Mathematische Unterschiede drücken die Betrachtung vor bzw. nach den Stößen aus. Bei einem konzentrierten Uratom-Fluß kann aber der zufällige Vektorwinkelerwartungswert <ß> jetzt im kleinen systemauflösenden Bereich liegen. Deshalb war vorn schon das Bild der Stromkreuzung verwendet worden. Diese führt in der Systemstreuung zu Instabilitäten und damit Systemauflösungen. Deren Größenordnung muß dazu natürlich im Bereich der Systembildungsstärke liegen. Nur die Wahrscheinlichkeit für das Auftreten der zur Elementarteilchenbildung (W^± und Z⁰) nötigen Energie liegt in der Größenordnung von 10^-11. Daraus ergibt sich die Schwäche des Kopplungsfaktors. Bei den normalerweise auftretenden virtuellen Vektorbosonen- bzw. Neutrino-Strömen wird nur selten statistisch eine solche Überlagerung erreicht, daß eine meßbare Wirkung eintritt.

Neutrinos haben notwendigerweise einen Vektorwinkelerwartungswert <ß> = 0. Sie existieren aber als davoneilende Restenergie. Nimmt man bei den Vektorbosonen ebenfalls <ß> = 0 an, muß der Systembildungseffekt aufgrund des kleinen Geschwindigkeitsunterschieds nahe c bzw. v^quer möglich sein. Andererseits kann der Zusammenhalt durch einen einseitig verschobenen Stoßachsenwinkel-Erwartungswert erzeugt werden. Das ist durch eine allgemeine Verwirbelung bzw. einen Stoßrhythmus im Normalraum denkbar (Chiralität). Die Untersuchung des dazu führenden stochastischen Prozesses muß aber der zu entwickelnden Theorie überlassen werden.

Als beste Methode zur Beschreibung und Berechnung von Vorgängen der elektroschwachen Wechselwirkung haben sich die Pfadintegrale der Propagator-Theorie, besser bekannt als Feynman-Graphen, bewährt. Diese entsprechen in intuitiver Weise gerade den betrachteten Uratom-Flüssen. Hier können ihre Darstellungen voll ausgeschöpft werden, weil der Kopplungsfaktor sehr klein ist. Auch Streuungsmatrizen bzw. Reaktionsmatrizen der analytischen S-Matrix-Theorie (vgl z.B. in [F 89] erhalten einen tieferen inneren Sinn.

Literatur:
[B 81] Becher, Böhm, Joos; Eichtheorien der starken und elektroschwachen Wechselwirkung; Stuttgart 1981
[B 86] Bethge, K, Schröder, U.; Elementarteilchen und ihre Wechselwirkungen; Darmstadt 1986
[F 89] Fachlexikon ABC Physik; 2 Bde; Harri Deutsch Thun, Frankfurt/M, 1989
 
 

Inhalt

Grafik

vorheriges

nächstes

Links

Stichworte (Ende)

Wiese, Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace, Porec 2000
Uratom (Anfang)