6.2 Starke Wechselwirkung
Hadronische Materie ist durch den Systembildungseffekt hoch konzentriert. Systeminnere, vom Normalraumdruck ( h) unabhängige Ströme, lassen im Schattenbereich die Ansammlung weiterer Uratome zu. Dieser van-der-Waals-Rest der Systembildung besitzt somit eine Stärke im Größenordnungsbereich der systeminneren Effekte. Nach außen ergibt sich wegen der Stabilität gegenüber dem Vakuum bei den "farbigen" Dichte- bzw. Geschwindigkeitsvektorströmen Neutralität, was mit "weißer Farbe" oder "Summe der Innenwinkel im Dreieck beträgt 180°" umschrieben werden kann. Nicht zusammenpassende innere Uratom-Ströme führen deshalb zur Aufblähung und schnellen Auflösung aufgrund oder besser trotz starker Wechselwirkung.
Der Größenordnungsbereich wird durch die freien Weglängen diktiert, welche von außen durch die Normalraumeigenschaft h und durch c festgelegt sind. Obwohl sich hier nicht die Frage nach dem Quarkeinschluß stellt, kann die Analogie zum MIT-Bag Modell (vgl. z.B. in [GS 89], S. 204ff), bei dem dieser durch das Modell des äußeren Vakuumdruckes auf den Bag erklärt wird, herangezogen werden. Mit wachsender Wechselwirkungsenergie abnehmende effektive interne Kopplung wird durch die direkte Streuung der Uratome aneinander verständlich.
Beschreibungsmöglichkeiten durch die QCD und die Stromalgebra wurden schon vorn erwähnt. Offensichtlich sind den komplizierten mathematischen Strukturen, welchen die bekannten Namen (Quark, Farbe, Isospin,...) gegeben wurden, nun aber einfache Uratomflüsse zuzuordnen.
Bei den systeminternen Urmaterieströmen der Hadronen spielt das äußere Gleichgewicht nicht mehr die entscheidende Rolle. Stoßwahrscheinlichkeit und damit stochastische Uratombewegungen im Systeminneren sind rein lokal, hängen also nur von der näheren Umgebung ab. Es gibt ja keine Fernwirkung.
Nimmt man als Maßnormierung den direkten Stoß einer durchschnittlichen Normalraumkugel, kann auch der Systembildung, zumindest bei stabilen Systemen, das durchschnittliche Stärkemaß 1 zugeordnet werden. Der Stärkefaktor von inneren Kräften muß aus lokalen Beschleunigungen geschlossen werden. Diese wiederum können sich statistisch nur aus den Durchschnittswerten der bei den Stößen entstehenden Geschwindigkeitsunterschiede ergeben.
Selbst unter der Annahme, daß auch im dichten
Medium parallele Bahnen weiterhin gleich wahrscheinlich sind, kann der
durchschnittliche Stoßachsenwinkel von 45° bei der Abschätzung
der erzeugten Geschwindigkeitsunterschieds-Erwartungswerte, also die Stoßachsen-
(Wahrscheinlichkeits-)Formel in die Stoßformel
eingesetzt werden. Besitzen die beiden Stoßpartner vor dem Stoß
den gleichen Geschwindigkeitsbetrag 1, ergibt
sich bei 90° Vektorwinkel auf einem Partner die neue Geschwindigkeit
sqrt(2), während der andere im Laborsystem zur Ruhe kommt. Läßt
man einen veränderten systeminneren Vektor immer wieder mit dem Normalraumvektor
der Länge 1 zusammenstoßen, streben die Werte gegen 1
+ sqrt(2) bzw. sqrt(2)-1. Kann nun wegen der großen
Dichte auch der zweite Stoßpartner bereits ein von 1 abweichender
systeminnerer Geschwindigkeitsvektor sein, wird der Veränderungsfaktor
noch größer. Als Schranke wirkt dabei die Raumauffüllung
in Verbindung mit der bei hohen Geschwindigkeiten stärkeren Fluktuation.
Durch diese kann die Geschwindigkeit von systeminneren Vektorflüssen
nicht über alle Grenzen wachsen. So ergibt sich die Stärke des
tatsächlich beobachtbaren Kopplungsfaktors der starken Wechselwirkung
von 1....15. Für fast alle Stoßachsenwinkel alpha
verläuft dann
f(<ß>) mit <ß> >>
0 im Positiven, woraus
eine verstärkte Geschwindigkeitsdifferenz-Zunahme folgt. Wesentlich
für die systembildende starke Wechselwirkung ist dabei sicher die
Abweichung
der Stoßvektorwinkel vom Normalraum-Erwartungswert. Deren Größe
liegt zwischen Null und 90° bzw. auch -90°. Der zur Systembildung
führende Mindestwert bei einem annehmbaren systeminternen Geschwindigkeitsdifferenz-Erwartungswert
richtet sich nach dem Stärkeverhältnis. Möglicherweise lassen
sich diese Winkelbereiche auch experimentell erschließen.
Auf einer Dichtezunahme durch Querstöße beruht auch der Systembildungseffekt von Leptonen. Ein Stoßpartner ist jedoch immer aus dem umliegenden Normalraum zu erwarten. Das eine Stoßzentrum spannt dabei mit den freien Weglängen zu den nächsten Normalraumstößen einen relativ großen Systembereich auf. In diesem Bereich herrscht Stoßgleichgewicht mit dem Normalraum. Es können keine zusätzlichen Uratome in einem Schattenbereich gesammelt werden. In der einfachen Niederenergie-Streuung prallen die Uratome der betroffenen Systeme voneinander ab. Die starke Wechselwirkung reagiert deshalb nicht auf Leptonen.
Nochmals betont werden soll aber, daß bei der starken Wechselwirkung auftretende systeminnere Ströme für sich allein im Normalraum nicht stabil sein könnten. Erforderlich ist die innere Wechselwirkung. Dabei tritt ein lokales Potential für die bei Experimenten auftretenden Teilmengen von Uratomen der beteiligten und aneinander streuenden Elementarteilchen auf. Dieses muß nach dem hier behandelten Modell somit ungefähr die Form
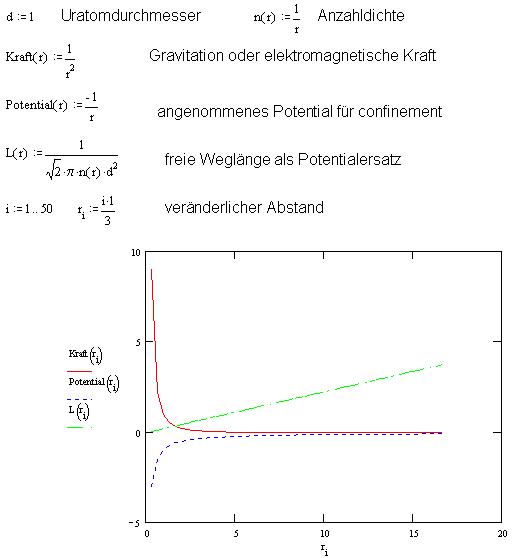
Literatur:
[B 81] Becher, Böhm, Joos; Eichtheorien der starken
und elektroschwachen Wechselwirkung;
Stuttgart 1981
[GS 89] Greiner, W., Schäfer, A.; Quantenchromodynamik;
Thun, Frankfurt a. M. 1989
[L 89] Lucha, W., Schöberl, F.; Die starke Wechselwirkung,
eine Einführung in nichtrelativistische Potentialmodelle; Mannheim/
Wien/ Zürich 1989
[R 91] Roepstorff, Gert; Pfadintegrale in der Quantenphysik;
Vieweg Braunschweig 1991
|
|
|
|
|
|