| |
In der Diskret formulierten Standardphysik werden sehr kleine Objekte im Substrat des Vakuums postuliert, welche eine äquivalente Beschreibung zu den Standardmodellen von Elementarteilchen und Kosmologie ermöglichen. Die Formulierung mit den immateriellen Abständen von Uratomen entspricht der Standardphysik mit einem einheitlichen Abschneidefaktor. |
Grundidee: Physikalische Felder werden aus Uratomen gebildet. |
|
vorheriges Uratom |
Die Entwicklung des Universums
untersucht auch der
Excellence
Cluster Universe |
DOM |
| Welche Kriterien führen zur Akzeptanz
eines neuen Ansatzes? Bessere Ergebnisse als andere
Alternativen. |
95 % des Universums
sind unerklärt (Dunkel),
95% der Menschen glauben,
dass es
Unerklärbares gibt.
|
WIKIPEDIA kann zu einer Allumfassenden Theorie (AUT) werden. |
|
eigene
Rechenwege zur FSK |
Eigene alte Dokumente
auf dem
Weg dahin |
Struktron.de |
Diskret formulierte Standardphysik
Erzeugung von Dunkler Materie und Energie (.pdf des ersten Ansatzes)Diskret formulierte Standardphysik 1.
Existenz bewegter diskreter Objekte (Uratome in
der Größenordnung der Plancklänge, verhindern
Singularitäten)
2. Orte und Zeitpunkte von Ereignissen (erzeugen die Möglichkeit von Superpositionen) 3. Stoßtransformationen (erzeugen durch Selbstwechselwirkung im Substrat wichtige Symmetrien) 4. Gültigkeit von Erhaltungssätzen (für Energie und Impulse entstehen einfach nach dem Satz von Pythagoras) 5. Erzeugung von Geschwindigkeits-Verteilungen (Maxwell-Boltzmann-Verteilung entsteht durch Thermalisierung) 6. Verteilung der freien Weglängen (sind unabhängig von Geschwindigkeiten und regeln die Wahrscheinlichkeit für Ereignisse) 7. Materie-Ansammlung (Verklumpung)1.Anfangs-Mechanismus von Strukturbildung 2.Bildung von Asymmetrie 3.Gravitations-Mechanismus 8. Emission in die Umgebung (Dunkle Energie) (Bildung von Leerräumen mit Vergrößerung durchschnittlicher freier Weglängen) 9. Erste Strukturbildung durch Materieansammlung (Dunkle Materie) (Gravitation mit Verkleinerung der freien Weglängen durch maximale Aufenthaltsdauer zweier Uratome in der Nähe zueinander.) 10. maximale Verklumpung (dichte Kugelpackung) bis hierher DUNKEL ab hier BUNT
Diskretes Standard
Modell
(älteres .pdf)
|
12. Kondensation zu Elementarteilchen Die langsame Verklumpung,
deren zeitlicher Verlauf sich berechnen lassen sollte,
im Extremfall sogar ein schneller Kollaps, wird erst
nahe der maximalen Auffüllung gestoppt. Die Ansammlung
müsste bei einem Urknall-Szenario alle sichtbare und
vermutete Dunkle Materie enthalten, welche hier nur
aus Uratomen besteht. Ähnliches kann bei der
Verschmelzung von kompakten Ansammlungen stattfinden.18
Wegen des kleinen Effektes der Gravitation sind aber
langsame Ansammlungen wahrscheinlicher. Diese brauchen
noch keine baryonische Materie zu enthalten und ihre
Beobachtbarkeit ist deshalb erschwert. Galaxien dunkler
Materie könnten so schwere kalte Zentren
erhalten, die dann Jets überflüssiger
Materie mit heißer Oberfläche entwickeln. Deren
Durchmesser sollte beobachtbar sein. In den Jets erfolgt
vermutlich eine asymmetrische Kondensation von
Elementarteilchen normaler Materie. In Oberflächennähe
würden bei Stößen erzeugte nicht in die Struktur
passende Geschwindigkeitsbeträge wegen fehlender
Stoßpartner nach außen entweichen, auch mit
Überlichtgeschwindigkeit. Das wäre im Durchschnitt
dunkle Energie, welche kleine Strukturen der Ansammlung
mitreißt. Die dabei erfolgende (asymmetrische) Elementarteilchenbildung
erzeugt bei der Strahlaufweitung zuerst Neutronen und
dann bei weiterer Ausdünnung daraus Protonen und
Elektronen, aber keine Antimaterie.
Stabile membranartige Hüllen gegenüber der Umgebung können nur entstehen, wenn in den umschlossenen Bereich gleich viele Uratome aus allen Richtungen eindringen, wie diesen verlassen. Bei einem Jet, aber auch bei der rings um eine Verklumpung erfolgenden Expansion werden weg fliegende Uratome nur durch Stöße am Weiterfliegen gehindert. Wäre die Umgebung ganz leer, würden solche Stöße auf vorher weg geflogene Uratome nur wegen unterschiedlicher Geschwindigkeiten stattfinden. Diese besitzen eine Maxwell-Boltzmannsche Geschwindigkeitsverteilung (Abbildung 5, Abschnitt 5). In einer älteren Umgebung erzeugen Stöße Durchschnittswerte von Geschwindigkeitsbeträgen und freien Weglängen. Aus der Verklumpung muss demnach eine Anpassung an diese erfolgen. Dabei können verschiedene Extremwerte mit unterschiedlichen Stabilitäten auftreten.  Abbildung 14: Fluktuationen bei der
Expansion verursachen die Entstehung stabiler
Strukturen.
Der untere Teil in Abbildung 14
soll eine dichte Ansammlung von Uratomen
darstellen, welche aus dem Zentrum der Verklumpung
so heraus kommen, dass sich die freien Weglängen
wegen fehlender Stoßpartner vergrößern. Dabei wird
die innere Verwirbelung mit genommen. Im Randbereich
wird ein thermodynamisches Gleichgewicht
anfangs auch gegenüber gerade erst aus der
Verklumpung dort hin gelangten Uratomen gebildet.
Das ermöglicht die Entstehung von schwereren
Strukturen. Diese bleiben aber wegen der Änderung
ihrer Umgebung durch Thermalisierung nur insoweit
stabil, als in ihnen Außenbereiche ein
thermodynamisches Gleichgewicht zur Umgebung
besitzen. Bei dessen Störung sollte es zum Zerfall
in einzelne für sich stabile Konstituenten,
wie in Abbildung 13 angedeutet, kommen.
Abbildung 8 zeigt, dass bei Stößen normalerweise
größere und kleinere Geschwindigkeitsvektoren
entstehen. Einer von beiden passt besser zu einer
Anfangsströmung und verstärkt diese, wenn ein neu
hinzukommendes Uratom nicht von einem vorhandenen
unterschieden wird. Wenn nun die Strömung eine außen
weniger dichte Umgebung besitzt, können
Anfangswirbel sich nach außen von der Hauptströmung
entfernen. Beim durchschnittlichen Stoßachsenwinkel
von 45° erfolgt eine Drehung um 90°. Beide
Drehrichtungen kommen in gleicher Häufigkeit vor,
wodurch die Symmetrie der Spins erzeugt wird. Im
Durchschnitt entstehen dabei sogar sich orthogonal
voneinander entfernende Ströme. Das wird auch bei
vielen Turbulenzen beobachtet. Die Korrespondenz
anschaulicher Vorstellungen von inneren Bewegungen
in Elementarteilchen zu denen von beobachteten
Strömungen darf allerdings nicht überstrapaziert
werden. In Elementarteilchen begrenzen die freien
Weglängen und die Streuung der vorkommenden Winkel
diese Analogie, welche nur bei der heißen Bildung
von Elementarteilchen in Stoßversuchen sinnvoll
erscheint. Die Unabhängigkeit der freien Weglängen
von den Geschwindigkeiten ermöglicht da eine
Symmetrie der Erzeugung von Teilchen und
Antiteilchen mit gleicher Masse. Aus kalten
Ansammlungen können positive und negative
Teilchen vermutlich ohne diese
Teilchen-Antiteilchen-Symmetrie
materialisieren (kondensieren). Nur die absorbierten
oder emittierten Geschwindigkeitsvektoren sind das
entscheidende Merkmal für die Ladung, wie es bei der
Erzeugung der Feinstrukturkonstante diskutiert wird.
Orthogonal zu einem Systemzentrum kann sich eine
Ausdehnung oder Schrumpfung ergeben oder das System
bleibt stabil. Die dafür entscheidenden Bedingungen
sind gesucht, beitragen könnte eine maximal mögliche
Auffüllung.
Nach dem verbalen und skizzenhaften Versuch die Vorgänge dabei zu verstehen, müssen diese zuerst mit Mastergleichungen und dann auch im üblichen Lagrange-Formalismus formuliert werden.# Hier werden nur Ideen zur Lösung dieser großen Aufgabe vorgestellt. Vor allem muss ein Mechanismus angedacht werden, welcher die Stabilität der Protonen mit ihrer 1.836 fachen Masse von Elektronen ermöglicht. Den Erzeugungs- und Vernichtungsoperatoren der Feldtheorien sollten Selbstwechselwirkungen im betrachteten Substrat zugeordnet werden können. Die Entdeckung von Galaxien mit fast nur kalter dunkler Materie (CDM) deutet auf diese Entstehungsmöglichkeit hin. Im Zentrum gäbe es eine Grenze maximaler Auffüllung, welche auch zu Gravasternen führen kann aber üblicherweise als schwarzes Loch bezeichnet wird. Photonen gäbe es bis zum Ereignishorizont nicht. Dunkle Materie zur Erklärung der Dynamik, ist Bestandteil der Gesamtstruktur. Alles befindet sich im freien Fall ums Zentrum, wobei Sterne in der Strömung mit schwimmen. Selbst ohne baryonische Materie sollten solche Vorläufer von Galaxien existieren.19 Das könnte auch bei einem Urknall erfolgt sein. Falls sich die Rotverschiebung aber anders, z.B. durch eine ständige Absorption in normaler Materie, mit Verdünnung und Durchschnittsgeschwindigkeitserhöhung in der Umgebung, erklären lässt, bliebe der Effekt zumindest denkbar als eine Art Urknall bei der Galaxienbildung.20 Der Anfangszustand zur Bildung der Strukturen kann in einer heißen oder kalten Ansammlung liegen, wobei heiße Strömungen momentan besser untersucht sind (LHC, Turbulenzen,…). Die lokale Stabilität muss auch das Pauli-Prinzip erzeugen. Aber wie lassen sich die unterschiedlichen mehr oder weniger stabilen Strukturen, für den Anfang wenigstens verbal, erklären? Freie WeglängenBestandteile der großräumigen kosmischen Strukturen sind im Kleinen offensichtlich Phänomene, welche erfolgreich mit dem Standardmodell der Elementarteilchen beschrieben werden. Wesentlich ist in diesem das Auftreten von periodischen Funktionen, welche mit der Stabilität der Strukturen (vor allem Elementarteilchen) zusammenhängen. Diese können in der diskreten Erweiterung nur durch Superposition und Stöße beeinflusst werden. Bei orthogonalen Stößen entstehen größere Geschwindigkeitsunterschiede. Die freien Weglängen sind unabhängig von den Geschwindigkeiten. Sie werden allein von der Anzahldichte nach der Formel (2) bestimmt. In gravitativ erzeugten dichten Ansammlungen werden deshalb kleine freie Weglängen vorherrschen. Diese freien Weglängen können direkt in der Comptonwellenlänge elementarer stabiler Ansammlungen vermutet werden: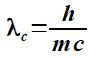 (14) (14)Die darin vorkommenden Größen
h und c werden weiter unten erklärt. Strukturen,
denen das Phänomen von Stabilität gegenüber der
Umgebung und eine Comptonwellenlänge zugeordnet
wird, könnten so eine systeminterne freie
Weglänge dieser Größenordnung besitzen. Das
sollte zumindest orthogonal zur Strömung
mit einer kleinen Durchschnittsgeschwindigkeit
verbunden sein, weil diese außerhalb der
Ansammlungen hoch ist. Solche Strukturen werden
als Elementarteilchen bezeichnet. Die Quelle
deren häufigster Erzeugung liegt deshalb
vermutlich in den durch Gravitation erzeugten
Ansammlungen, möglicherweise auch des gesamten
bekannten Universums. Auch kalte dunkle Materie
kommt dafür neben heißen Strömungen baryonischer
Materie infrage. Bei der heißen Bildung
kommen Teilchen und Antiteilchen
gleich häufig vor und müssen wegen der
Unabhängigkeit der freien Weglängen von den
Geschwindigkeiten die gleiche Masse
besitzen, obwohl kleinere oder größere als
durchschnittliche Geschwindigkeitsvektoren
emittiert werden.
Zentren beginnender Strukturbildung in dichten Ansammlungen verlagern sich nach dort, wo weniger Stöße zu erwarten sind. Weil bei Stößen Drehungen der Relativgeschwindigkeiten erzeugt werden, entsteht möglicherweise eine Asymmetrie von rechts- und linksdrehenden Strukturen. Abstoßung (Bewegung dorthin, wo weniger Stöße erfolgen) solcher noch virtuellen Strukturzentren kann dann in heißen Strömungen (Beschleunigerexperimente) zur paarweisen Kondensation von Wirbeln führen, welche in ihrer Umgebung eine gewisse Stabilität, also Lebenserwartung, besitzen. Beschreibende Funktionen sollten Periodizität aufweisen und so für eine Periode berechenbare Werte der Anzahl, also Masse, liefern. Ursache für den Zusammenhalt von Strukturen ist die innere freie Weglänge. Die Superposition von deren Wahrscheinlichkeiten könnte durch die starke Wechselwirkung beschrieben werden, welcher eine Kraft der Größenordnung 1 zugeordnet wird. Für Stabilität muss die Stoßfrequenz mit der Umgebung übereinstimmen, im Sinn der Erfüllung einer Mastergleichung. Das kann wegen der unterschiedlichen möglichen Ladungen (größere und kleinere Geschwindigkeiten nach außen), andererseits aber immer gleichen Masse (Anzahl der zur Struktur gehörenden Uratome) vermutlich nur durch die orthogonalen Komponenten erreicht werden. Daraus folgt eine erforderliche Querbewegung in der Struktur, welche mit dem Spin identifiziert werden soll. In der Paarvernichtung treffen zwei identische, nur phasenverschobene Wellenfunktionen aufeinander. Die Masse ist gleich, die Geschwindigkeiten sind aber nach Durchschnittsgrößen unterschiedlich strukturiert, wodurch die gegenseitige Anziehung entsteht. Wegen der Stabilität im betrachteten Substrat passen die Wellen mit ihren identischen Comptonwellenlängen genau ineinander, nur haben die zugeordneten inneren Geschwindigkeiten, welche die freien Weglängen nicht beeinflussen, nach außen entgegengesetzte Abweichungen von der Durchschnittsgeschwindigkeit (Ladung). Die Gesamtmasse bzw. Energie bestimmt die Comptonwellenlänge. Eine wesentliche stabilitätsbildende Eigenschaft ist die Stoßfrequenz gegenüber dem Substrat der Umgebung. Bei der scheinbaren Auslöschung bleibt aber die Energie erhalten, was zur Erklärung einer sich mit Lichtgeschwindigkeit ausbreitenden Störung beiträgt. Dieser Prozess kann auch umgekehrt ablaufen. Die bessere Zugehörigkeit zu Strömungen führt zur Absorption passender Vektoren, diese finden deshalb zueinander. Die Wahrscheinlichkeit der einzelnen Bewegungen ist dafür größer. Drehimpuls und SpinWeil bekannt ist, dass Elementarteilchen sowohl Elementarladungen als auch magnetische Momente erzeugen, ohne Energie zu verbrauchen, sind elementare dafür erforderliche Mechanismen zu suchen. Bei Vorbeiflügen ändern sich Relativgeschwindigkeiten nicht, deshalb bleiben auch (Bahn-) Drehimpulse erhalten. Einzelne Stöße lassen Relativgeschwindigkeitsbeträge unverändert, die Wirkung ist die einer Drehung und daraus sollte dann der Spin folgen. Bekannt ist, dass bei jedem Stoß die Relativgeschwindigkeit gedreht wird (Abbildung 8).Im Gegensatz zu starren Körpern, bei denen der Zusammenhalt der rotierenden Materie nicht hinterfragt wird, muss dieser hier erklärt werden. Das Füllen einer Sphäre mit bewegten diskreten Objekten lässt sich durch eine endliche Anzahl zugeordneter Raumzeit-Punkte beschreiben. Eine Gleichverteilung und isotrope Richtungen der MB-verteilten Geschwindigkeiten würde dem umgebenden Normalraum entsprechen. Den Bewegungen könnte nun eine Drehung überlagert sein, welche der Drehung einer vollen Kugel entspricht. Das sich ergebende Drehmoment wäre dann das der Vollkugel, weil sich die ursprünglichen Bewegungen des Normalraums (Vakuums) weg mitteln lassen. Die innere Stoßzone benötigt für eine Stabilität ein internes Stoßgleichgewicht und die äußere Zone gegenüber ihrer Umgebung, also dem Vakuum. In beiden Fällen müssen demnach die Stoßfrequenzen, also Geschwindigkeitsbetrag mal Dichte oder Geschwindigkeitsbetrag durch freie Weglänge, der Umgebung entsprechen. Das ist auf verschiedene Arten möglich. Berücksichtigt werden muss dabei der Hintergrund des Vakuums, weil in dem betrachteten Bereich aus diesem selbst hinein geratene Uratome nicht von äußeren unterschieden werden können. Im einfachsten Fall kann ein inneres Stoßzentrum von den Uratomen, welche sich im Stoßgleichgewicht mit der Umgebung befinden, gebildet werden. Der gesamte Bereich des Systems erzeugt dann von der Umgebung abweichende Geschwindigkeitsbeträge, also Ladung und einen Spin ½. In Experimenten kann die Stoßzone fast punktförmig erscheinen. Deren Mittelwert ist es auf jeden Fall. Die Wahrscheinlichkeit des Stoßachsenwinkels (dünne durchgezogene Linie in Abbildung 8) ist zur Richtung der Relativgeschwindigkeit symmetrisch, weil im normalen Raum parallele Flugbahnen als gleich wahrscheinlich angenommen werden. Bei jedem Stoß bleibt der Relativgeschwindigkeitsbetrag unverändert, deren Richtung ändert sich aber in Abhängigkeit von der Stoßachse, was jeweils einer Drehung entspricht. Dieser Drehung kann auch ein axialer Vektor (rot gestrichelt) zugeordnet werden, wenn eine Drehachse definiert ist, deren Abstand ins Kreuzprodukt mit der Winkelgeschwindigkeit ein geht. Problem ist jetzt die Zuordnung einer Winkelgeschwindigkeit zu der spontanen Drehung beim Stoß. Das erfordert eine Durchschnittsbildung vieler Stöße. Ohne Drehachse, also lediglich mit der Annahme eines Zentrums der Ansammlung, kann trotzdem der Abstand von diesem zur Bildung eines Pseudovektors verwendet werden. Als mathematische Begründung, wird vorläufig für einen Stoß dieser rot gestrichelte, zur Stoßachse parallele Anteil der Relativgeschwindigkeit als Winkelgeschwindigkeit angenommen. Dieser entspricht ½ des Pseudovektors (Axialvektor) der Änderung der Relativgeschwindigkeit, welcher über alle zum System gehörenden Stöße eine Art Drehimpuls beschreibt, welche Spin genannt wird. Innerhalb der Strömung, welche als Elementarteilchen interpretiert werden soll, finden nach Stößen besser zu der Strömung passende Komponenten zueinander, weil sie länger näher beisammen bleiben. Die vorkommenden Vektorwinkel mit einem von Null abweichenden Mittelwert wirken sich auf die Symmetrie der entstehenden Stoßachsenwinkel aus. Parallel zur Relativgeschwindigkeit gleich wahrscheinliche Flugbahnen können nicht einfach voraus gesetzt werden. Im Systeminneren kann eine Asymmetrie der Stoßachsenwinkel vorkommen. Vom Systemzentrum aus überlagern sternförmig nach außen gerichtete Bahnen die im Normalraum übliche Gleichwahrscheinlichkeit paralleler Flugbahnen. Wegen fehlender Drehachse des Systems streuen aber die Berührungspunkte jeweils über einen ganzen Kreis auf der Oberfläche der betrachteten Ansammlung. Aus einem kleinen Winkelbereich sind von außen keine Asymmetrien der Herkunft von Stoßpartnern zu erwarten, so dass weiterhin annähernd gleich wahrscheinliche parallele Flugbahnen zu vermuten sind. Der Faktor ½ beim Spin kann auch auf das Fehlen von Drehachsen zurückgeführt werden, was sich als Abschirmung oder in entgegengesetzter Richtung zur Beschreibung fliegender Hälften der Systemmasse bezeichnen lässt. Orthogonal zu den betrachteten Relativgeschwindigkeiten ergeben sich die größten Änderungen von freien Weglängen (Dichte), weil orthogonale Stöße am häufigsten sind. In der Mastergleichung (9) kann deshalb die große Dichte in Verbindung mit einer kleinen Durchschnittsgeschwindigkeit das erforderliche Stoßgleichgewicht zur Umgebung erzeugen. Mit mehreren wandernden inneren Stoßzentren (Quarks) wird eine Struktur aufgespannt, bei der die durchschnittliche freie Weglänge von deren sehr großer Dichte und den Wegen bis zu Stößen mit Uratomen aus dem Substrat der Umgebung gebildet wird. Hauptsächlich können Stöße mit dem oder den anderen Stoßzentren stattfinden, also nicht mit der dünnen Umgebung (Vakuum). Das erklärt die viel höhere Masse solcher Elementarteilchen.21 Damit zusammenhängende Wahrscheinlichkeiten können superponieren und erklären die Additivität von Spin und Bahndrehimpulsen. Aus Systemen mit Spin ½ lassen sich deshalb alle anderen kombinieren. Leptonen und Quarks (Spin ½ Fermionen)Elementarteilchen sind Strukturen welche
durchs Standardmodell beschrieben werden.
Fermionen besitzen den Spin ½. Deren übliche
tabellarische Darstellung bedarf in der
diskreten Erweiterung vor allem einer
Erklärung offener Fragen dazu, wie
beispielsweise zum Hierarchieproblem oder zu
den drei auftretenden Generationen. Die
Symmetrie von Materie und Antimaterie kann
durch die Unabhängigkeit der freien Weglängen
von den Geschwindigkeiten veranschaulicht
werden, weil diese dabei die Größe der
Struktur und deren Stabilität erzeugen.
Deshalb ist hier ein Ansatz mit
Wahrscheinlichkeiten für die auftretenden
Strömungen in den Elementarteilchen gesucht,
welcher für numerische Lösungen das
Hilfsmittel der Inversionsmethode verwenden
kann. Eine Selektion von größeren oder
kleineren systembildenden Vektoren, wie das in
Abbildung 8 angedeutet ist, liefert den Ansatz
für die Beschreibung von Ladung und Spin in
solchen Ansammlungen. Als Problem ist das
vergleichbar mit der Berechnung von
Turbulenzen, welches immer noch nicht
vollständig gelöst ist. Deshalb sollen nur
einige grundsätzliche Gedanken für diese große
Aufgabe angesprochen werden, die über die
gemeinsame Eigenschaft des Spins ½ hinaus
gehen. BosonenEin rätselhaftes Elementarteilchen ist auch das Photon. Es führte zur Entwicklung von Quanten- und Relativitätstheorie und ist doch nicht vollständig verstanden. Wichtig für seine Erklärung in der diskreten Erweiterung wird die vorn erwähnte Vernachlässigung von orthogonalen Geschwindigkeitskomponenten. Diesen können transversale Schwingungen zugeordnet werden. In Störungen (Photonen) wird die Richtungsstabilität vermutlich durch die perfekte Symmetrie der Geschwindigkeitsüberträge in Stoßachsenrichtung erzeugt. Das massenhafte Auftreten von Stößen erzeugt dann im Substrat die Periodizität, welche sich neben der Erzeugung auch nach dessen Eigenschaften richtet. Dabei kann im Ausbreitungsgebiet eine größere Anzahl vorkommen, als im umgebenden Vakuum orthogonal zur Ausbreitungsrichtung, also zum Poynting-Vektor, (z.B. bei Gammaquanten sehr viele). Dem entsprechen nur orthogonale Vektorkomponenten, also Schwingungen. Das lässt auch sehr langwellige und kurzwellige Photonen stabil bleiben. Bei den Stößen während der Ausbreitung sind die vorkommenden Berührungswinkel (Stoßachsenwinkel) sehr symmetrisch und wiederholen sich deshalb im Durchschnitt perfekt periodisch (Abbildung 7), wie es mit der Wellengleichung ausgedrückt wird.Die Erzeugung, z.B. am Doppelspalt, verdeutlicht den Einfluss orthogonaler Komponenten. Diese können in das umgebende Substrat fluktuieren und sorgen für den transversalen Charakter der Wellen. Dadurch ist auch die Beziehung von Energie und Wellenlänge (E=h/λ) erklärbar. Die freie Weglänge im Medium spielt keine Rolle. Weshalb in einem beleuchteten Raum von jedem Punkt aus der gleiche Eindruck stabil bleibt, ist vermutlich erst durch die Rückkopplungen eines holografischen Einflusses zu erklären. In Bereichen hinter einem Ereignishorizont großer Ansammlungen gibt es möglicherweise, wie auch in dunkler Materie, keine Strukturen, welche Photonen durch ihre Periodizität entstehen lassen. Weitere Bosonen sind ähnlich zu betrachten. Transversale Einflüsse erzeugen die Möglichkeit sehr energiereicher Bosonen. Wellenlänge und orthogonale „Einflusslänge“ ergeben Raumzellen mit zugehörigem Inhalt der betrachteten Strukturen. HierarchieproblemIn der Kosmologie werden Galaxien teilweise als Staub behandelt und die Wechselwirkungen dabei als direkte Stöße. Zwischen ganz Großem und dem hier postulierten Kleinen scheint ein gewisser Zusammenhang zu bestehen.24Bei der Beschreibung eines elementaren Ereignisses in der Raumzeit, also dem Stoß von zwei Uratomen, ist das Produkt aller Wahrscheinlichkeiten (und-Verknüpfung) des zehndimensionalen Vektors oder eines Tensors mit zehn unabhängigen Parametern für den numerischen Wert maßgeblich. Die Superposition vieler solcher Werte kann dann einen dimensionslosen Zahlenfaktor ergeben. Kommt das zweite Uratom aus einer beliebigen entfernten Struktur, überlagern sich alle Wahrscheinlichkeiten. Durch die freien Weglängen, welche die Anzahldichte und dadurch die Masse bestimmen, kann sich die Stoßfrequenz ändern und eine resultierende Beschleunigung erfolgen. Einem ersten dimensionslosen Faktor für die freien Weglängen (Abschnitt 6) kann willkürlich die Größenordnung 1 zugeordnet werden. Bei der Expansion nimmt die Dichte von Ansammlungen ab. Bilden sich dabei stabile Strukturen, welche sich als Elementarteilchen bezeichne lassen, können Uratome von diesen absorbiert oder emittiert werden. Das erzeugt die normale geometrisch erklärbare Entfernungsabhängigkeit der Wechselwirkung in der näheren Umgebung in gleicher Größenordnung. Auch Strukturen mit der Ladungseigenschaft erzeugen noch eine Wechselwirkungsstärke in nahe bei dieser liegender Größenordnung 1/137. Die durchschnittliche Veränderung der freien Weglänge von Uratomen in Ansammlungen mit einem Stoßgleichgewicht nach außen liefert einen Zahlenfaktor, welcher, wie schon erwähnt, als Stärkeverhältnis für die Absorption, also Feinstrukturkonstante der Gravitation (Größenordnung 10-39) interpretiert werden kann. Mit diesem Zahlenfaktor lässt sich dann die Newtonsche oder Einsteinsche Gravitationskonstante G25 nach den bekannten Formeln26 ermitteln. Die Stöße selbst verzerren die Raumzeit, wie dieser Vorgang in der ART bezeichnet wird. In einer Materieansammlung sind alle Uratome im gleichen Maß an diesem Mechanismus beteiligt, weshalb die Stärke der Gravitation proportional zu deren Anzahl, also der Masse, ist. Energie, Impuls und in der Materie vorkommende Spannungen beeinflussen dabei die vorkommenden Ereignisse durch Raumzeitverzerrungen. Das drückt sich auch in der schwierigen Nachvollziehbarkeit der ART aus. Die Größenunterschiede zwischen den Wechselwirkungen sind demnach auf die Kleinheit der postulierten Uratome und die relativ zu diesen großen freien Weglängen zurückzuführen, was das Hierarchieproblem erklären sollte. |

Wiese, Albert Lothar: Struktur und Dynamik der Materie im Uratom-Modell, Porec/ Sarajevo 2000-2018