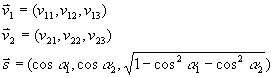Struktur und Dynamik der
Materie im
3 Beschreibung einer
Kugelmenge
3.1
Skalare bzw. binäre Alternativen
Nach der verbalen Beschreibung der Grundmenge durch
das Uratom-Axiom, ist für die
mathematische Darstellung die Existenz des, unserem Anschauungsraum
entsprechenden, dreidimensionalen Ortsraumes anzunehmen. Wegen der Bewegung
unendlich vieler Kugeln existiert darüber hinaus eine eindimensionale
kontinuierliche Parametermenge zur Beschreibung dieses Verhaltens, welche wir
Zeit nennen. Stehen wir dabei auf dem Standpunkt, dass nur die elementaren
Ereignisse, also Stöße, wichtig sind, wäre die Zeit abzählbar. Vielleicht
kommen wir so sogar zu einer Art Quantisierung, was aber hier nicht weiter
verfolgt werden kann.
Im vierdimensionalen, noch euklidischen,
Raum-Zeit-Kontinuum ergibt sich als elementarste Beschreibungsmöglichkeit des
Verhaltens einer sich darin bewegenden Menge von Kugeln (oder Uratomen bzw.
dichten Punktmengen), die Zuordnung von Uralternativen zu jedem
Raum-Zeit-Punkt, entsprechend dem Vorhandensein von Materie bzw.
"Etwas" oder dem Nichtvorhandensein. Diese Beschreibung könnte als
"skalares Feld" im 4-dimensionalen Vektorraum interpretiert werden.
Damit kann nun versucht werden, Relativitäts- und Quantentheorie sowie die
gesamte theoretische Physik abzuleiten (vgl. Betrachtungen über eine
Urtheorie in [W 85]).
Die Bewegung einer einzelnen Kugel lässt sich durch einen
Vektor
![]() R³ darstellen.
R³ darstellen.
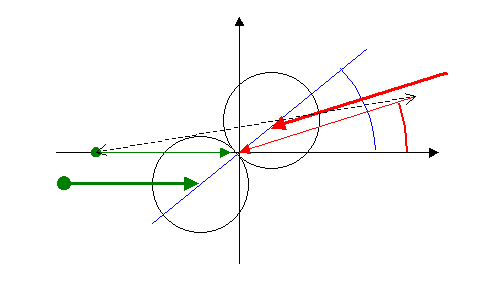
Zu einem Zusammenstoß gehören zwei bewegte Kugeln
bzw. Punktmengen, die einander berühren. Die Stoßachse entspricht der
Berührpunkt-Normale (blau). Diese kann in einem einmal gewählten
Koordinatensystem durch einen Einheitsvektor vollständig beschrieben werden.
Der Berührungspunkt und damit auch der (eigentlich zweidimensionale)
Stoßachsenwinkel (blau) kann maximal orthogonal zur Relativgeschwindigkeit
(gestrichelt) liegen. Mit gleichem Stoßvektorwinkel (rot) ist deshalb eine
Schar paralleler Flugbahnen aus diesem Bereich möglich.
Es seien
|
|
die zwei Stoßvektoren (grün und rot) und der Stoßachsenvektor (blau). |
Dann wird
![]()
die zur Stoßachse parallele
Geschwindigkeitskomponente des i-ten Stoßvektors und
![]()
die zur Stoßachse orthogonale
Geschwindigkeitskomponente des i-ten Stoßvektors.
Beim Zusammenstoß werden die parallelen
Geschwindigkeitskomponenten ausgetauscht, die orthogonalen bleiben auf der
jeweiligen Punktmenge erhalten:
![]()
Das ist die Stoßformel
(ausführlicher => klicken) des Uratom-Modells.
Der eigentliche Stoß entspricht also nach dem
Uratom-Axiom einer Drehung des Koordinatensystems in die Stoßachsenrichtung
und anschließende Vertauschung (Transposition) der zur Stoßachse parallelen
Komponenten. Dabei wird, unabhängig davon, welches gleichförmig bewegte
Koordinatensystem zugrunde gelegt wird, die Relativgeschwindigkeit an der
zur Stoßachse orthogonalen Ebene (Stoßebene) gespiegelt.
Wegen der angenommenen Existenz bewegter Punktmengen wird
(laienhaft) vermutet, dass damit auch der unitäre Raum der diesen
zuordenbaren Vektoren existiert. Die unendlich große Anzahl der Kugeln lässt
demnach sogar den für die mathematische Beschreibung oft verwendeten daraus
zu bildenden Hilbert-Raum existieren.
Stöße sind in diesem Raum aufgrund der Stoßformeln nicht
auf Anhieb als lineare Darstellungen von darin operierenden Gruppen zu
erkennen, was aber bewiesen werden sollte.
Bei der Verwendung eines 4-dimensionalen euklidischen
Raumes ergeben sich stückweise gerade Linien als eine Art von Weltlinien.
Die Geschwindigkeitsvektoren zeigen dabei als Tangentialvektoren immer in
Richtung der Linien. Richtungsänderungen (Knicke) entstehen bei der
Berührung zweier Linien. Im Gegensatz zum relativistischen Minkowski-Raum
gibt es hier aber noch keine Geschwindigkeitsbegrenzung und damit auch keinen
Lichtkegel.
Fürs Verständnis des Uratom-Modells sind die bis
zum Kapitelende folgenden Spekulationen (eines Laien und
Autodidakten) nicht von Bedeutung. Wichtig werden sie möglicherweise
bei der Entwicklung einer exakten Theorie.
3.3 Beschreibung durch
Matrizen bzw. Tensoren
Das Uratom-Axiom erlaubt nur Operatoren in der Grundmenge,
welche aus deren Teilmengen gebildet werden. Die Transformation eines
Geschwindigkeitsvektors einer harten Kugel kann nur durch einen Zusammenstoß
erfolgen. Ein Operator S der dies bewerkstelligt wird demnach wohl mit
dem zweiten Geschwindigkeitsvektor und den Stoßachsenwinkeln, welche eine
Drehmatrix D (aus der linearen Gruppe SO(3))
bilden, erzeugt.
Im bereits in die Stoßachsenrichtung gedrehten
Koordinatensystem (orthogonale Richtungen beliebig), kann dieser Operator
einfach durch eine Matrix S (welche wegen ihrer Invertierbarkeit
ebenfalls linear ist) dargestellt werden:
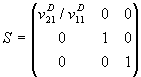
Die gesamte den Stoßgleichungen entsprechende
Transformation lautet dann
![]()
In welcher Form diese Transformationen zur
Beschreibung von Stößen in der zu entwickelnden Theorie sinnvoll ist, muss
noch geklärt werden. Eine einfache bijektive Zuordnung solcher Gebilde zu
Feld-Selbstwechselwirkungen ist denkbar.
Bereits aus dem Uratom-Axiom folgt, dass alle
Wechselwirkungen auf das Verhalten der elementaren Kugeln zurückführbar sein
müssen. Falls zwei bewegte Kugeln durch je einen Geschwindigkeitsvektor
dargestellt werden, stellt sich die Frage, wie man am günstigsten, die den
beiden Vektoren, kurz vor dem Stoß, zum Stoßzeitpunkt und kurz danach,
zugeordnete Situation, beschreiben kann. In die beiden bisherigen Stoßformeln
gingen zur Beschreibung eines Geschwindigkeitsvektors nach dem Stoß die
Komponenten beider Vektoren ein. Es bietet sich nun als laienhafte Idee an,
die jeweils zwei Geschwindigkeitsvektoren vor und nach dem Stoß in
entsprechenden komplexen Gebilden zusammenzufassen. Der Stoß muss dann durch
einen Operator ausgedrückt werden, welcher auf das Gebilde zum Zeitpunkt t-0
wirkt und das neue Gebilde zum Zeitpunkt t+0 erzeugt. Konstruiert
werden kann dieser aus den Stoßachsenwinkeln und einem Operator zum
Komponententausch.
Nehmen wir beispielsweise einen komplexen Vektor u
aus C3 mit drei Elementen, gebildet aus den beiden
Geschwindigkeitsvektoren, als komplexen Spaltenvektor und D wie
vorn als Drehmatrix der beiden unabhängigen Stoßachsenwinkel, so ergibt sich
jetzt ein komplexer Stoßoperator
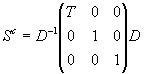 ,
,
mit T = I -1 als Operator,
welcher zuerst das Konjugiertkomplexe bildet und dann mit der imaginären
Einheit multipliziert. Als Stoßformel folgt deshalb
u´ = Sc u
Wegen T (T ) = i (T konjugiert ) = i ( -i ) = 1 sollte
der elementare Selbstwechselwirkungsoperator unitär und deshalb Sc
eine Berührungstransformation sein (vgl. z.B. in [F 89]). Außerdem ist er
wohl linear.
Wie bei der reellen Beschreibung stecken hier aber noch die
beiden Stoßachsenwinkel im Operator, d.h. in der Transformationsmatrix, wenn
auch bereits der ausgedachte Operator T vorkommt. Ziel ist es aber, das
betrachtete geometrische Gebilde mit sechs Freiheitsgraden um die zwei Winkel
auf acht zu erhöhen, so dass der gesamte Stoß mit zwei dreidimensionalen
Geschwindigkeitsvektoren und den beiden räumlichen Stoßachsenwinkeln durch
dieses beschrieben wird. Das könnte
ungefähr folgendermaßen aussehen, für die Anordnung der einzelnen Faktoren
existiert aber noch keine Idee:
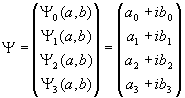
Dieses Gebilde erinnert stark an einen Diracschen
Bispinor. Dessen Transformationsverhalten gegenüber der für den Stoß
erforderlichen Drehung in Richtung der beiden, jetzt in dem Gebilde stehenden,
Winkel ist nicht so einfach wie bei den Vektoren. Es wird jedoch gehofft, dass
sich durch eine Transformation die beiden Winkel zu Null machen lassen und
sich das Invarianzverhalten eines Spinors ergibt. Wird beispielsweise
angenommen, dass die vierte Spinorkomponente den beiden Stoßachsenwinkeln
zugeordnet ist, so könnten durch eine Diracsche g- Matrix die beiden Winkel nicht zu Null gemacht werden, falls alle
vier Komponenten obigen Gebildes ungleich Null sind. Die Lösungen der
Dirac-Gleichung, welche Bispinoren sind, zeichnen sich aber gerade
dadurch aus, dass eine der Komponenten Null ist. Deshalb stellen diese wohl Stoßgebilde dar und eine Zuordnung von
Uratom-Bewegungen zu deren Komponenten würde eine Veranschaulichung
ermöglichen.
Die elementare Selbstwechselwirkung eines solchen
Gebildes, also die Einwirkung des jetzt um eine Dimension erweiterten,
ebenfalls unitären Selbstwechselwirkungsoperators, erfolgt dann wie im
dreidimensionalen Fall und stellt nur die Transposition zweier Komponenten
dar. Das Drehen in die Stoßachsenrichtung und Zurückdrehen soll aber durch
die beiden Winkel in dem Gebilde ausgedrückt werden, was für die
geometrische Deutung eines solchen Bispinors von Bedeutung wäre.
Die beiden Bispinorkomponenten sind bei der hier noch nicht
betrachteten Lorentz-Transformation wahrscheinlich getrennt wie
Elementarspinoren zu transformieren und vertauschen bei Spiegelungen ihre
Rolle. Bei den einfachen Drehungen erfolgt die Transformation deshalb mit der
Gruppe SU(2), welche mit der SO(3) isomorph ist.
Elementarspinoren beschreiben somit möglicherweise gerade
die durch eine bewegte Kugel verursachbare lokale Änderung an einer
betrachteten physikalischen Größe, hier also ebenfalls einer bewegten Kugel.
Sie können in gewissen, nicht so seltenen, Fällen aber auch nützlich sein,
wenn beispielsweise die beiden Geschwindigkeitsvektoren gerade die
Standardlängen aller Umliegenden annehmen und es sich um einen Frontalstoß
handelt. Bei diesem sind somit nur die beiden Winkel und deren Raumausrichtung
sowie die Stoßachsenwinkel von Bedeutung. Bei allen mathematischen
Beschreibungen ist selbstverständlich die dahinter steckende physikalische
Interpretation wichtig.
Für alle aus den Bispinoren mit Hilfe der Diracschen g-Matrizen (Bispintensoren)
bildbaren Kovarianten, d.h. bilinearen Tensorbildungen ([S 89] S.1459f) , ist
so auch eine geometrische Interpretation möglich. Je nach physikalischer
Problemstellung kann eine geeignete Beschreibung der Größen, welche die
jeweils zulässigen Messwerte annehmen können, durch Skalare, Vektoren,
Tensoren, Axialvektoren oder Pseudoinvarianten erfolgen. Uminterpretationen
der verschiedenen Komponenten erfolgen durch Transformationen aus der
unimodularen Gruppe SL(2,C), welche auch als C2
bezeichnet wird. Der Selbstwechselwirkungsoperator bewirkt eine,
lineare Veränderung des geometrischen Gebildes, welche jedoch bei
massenweisem Vorkommen durch Superposition, welche selbst lineare
Transformationen verwendet, verschleiert werden kann. Nur die Kenntnis der
Uratomgröße und Anzahldichte kann dieses Problem lösen.
Eine Transformation der Spinoren mit Hilfe der unimodularen
Matrizen (det U = 1) stellt keine interne Änderung des hier so definierten
Stoßgebildes dar, was allerdings noch zu beweisen ist.
Die bisher betrachteten Größen beschreiben die
Eigenschaft der Grundmenge an einem Raum-Zeit-Punkt. Ordnen wir jedem dieser
Punkte eine der vorn beschriebenen Eigenschaften zu, kommen wir auf
natürliche Weise zur Definition von Feldern.
Dabei verwirrt zunächst das Durcheinander der vorkommenden
Geschwindigkeiten und Winkel. Notgedrungen muss deshalb hier die
deterministische Betrachtungsweise verlassen werden.
Durch die Zuordnung von Erwartungswerten der skalaren,
vektoriellen, tensoriellen und spinoriellen Größen steht praktisch sofort
der gesamte Apparat der Feldtheorie zur Verfügung. Die Grundgrößen können
auf einfache geometrische Gebilde aus der Grundmenge zurückgeführt werden.
Aus der dargestellten Situation zum Zeitpunkt t-0 folgt nach der
Stoßformel eindeutig die Situation zum Zeitpunkt t+0. Auch die
weiteren Kovariantenbildungen mit Hilfe der Diracschen g- Matrizen lassen sich möglicherweise so veranschaulichen.
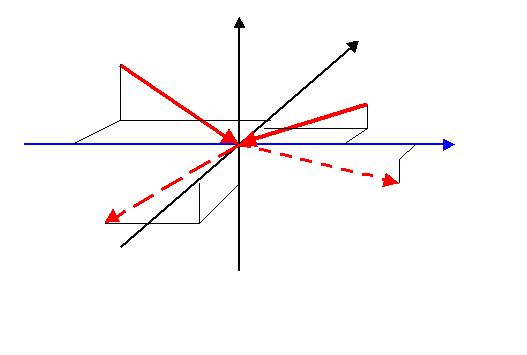
Zur vollständigen Beschreibung eines Stoßgebildes sind insgesamt 10
Parameter erforderlich. Je nach Anforderung können dies weniger werden.
Jeweils 3 Zahlen (z.B. Stoßvektorwinkel ß1 und ß2
sowie Geschwindigkeitsbetrag) stehen für die Geschwindigkeitsvektoren vor dem
Stoß, 2 für die Winkel der Stoßachse (Stoßachsenwinkel phi), welche hier zufällig in
x-Richtung (blau) liegt. Diese 8 Zahlen charakterisieren den vermuteten
Dirac-Spinor. Darüber hinaus sind 2 Parameter für die Anzahldichte, welche
sich durch das Verhältnis d / L ausdrückt, sinnvoll. Das ganze Stoßgebilde
wird natürlich in der Raumzeit betrachtet, wodurch noch 4 Zahlen (Zeit auch
imaginär) für die Felddarstellung hinzukommen, die zwar nicht das
eigentliche Stoßgebilde beschreiben, aber eine lokale Verzerrung der Raumzeit verursachen. Die
optimale Beschreibung ist sicher problemabhängig. Wegen der unmöglichen
Feinauflösung bis zu einzelnen Uratomen müssen in der Raumzeit
wahrscheinlichkeitstechnische Zusammenfassungen erfolgen.
Dabei wirkt noch vereinfachend, dass sicherlich nur die
Abweichungen von den Normalraumwerten zu physikalisch interessanten
Erscheinungen führen. Viele glatten normierten Kurven könnten als
Wahrscheinlichkeitsfunktionen, von sich bis zu Zusammenstößen jeweils
geradlinig bewegenden Kugeln, interpretiert werden (nach Normierung). Diesen
könnte man dann Feldlinien zuordnen.
Über die Verwendung von Erwartungswerten hinaus hat sich
in der Feldtheorie die Aufstellung von Wellengleichungen als nützlich
herausgestellt, welche eine Beschreibung der kontinuierlichen Änderung von
Erwartungswerten der Kovarianten bis zum Erreichen der alten Werte,
darstellen. Die komplexe Schrödingergleichung für eine solche Wellenfunktion
ist zwei gekoppelten reellen Gleichungen, für die Wirkungsfunktion und die
Amplitudenfunktion (vgl. [S 89] S.1280), äquivalent. Dadurch beschreibt auch
die Hamilton-Jacobi-Gleichung einen hier interpretierbaren Grenzfall.
Die Dirac-Theorie stellt dann die grundsätzliche Erweiterung auf alle
möglichen Kovarianten dar. Auch hier ist jedoch nur vom möglichen Vorkommen
solcher Strukturen in der Grundmenge die Rede.
Eine weitere Erweiterung ergibt sich durch das
Operatorenkalkül und die gleichzeitige Betrachtung von bis zu unendlich
vielen sich bewegenden Punktmengen durch die Verwendung von Hilberträumen.
Die Zuordnung von elementaren geometrischen Gebilden ist dabei auch hier
sicher prinzipiell möglich, weil ja die Konstruktion aus diesen, mit einer
Zuordnung zur Raumzeit, erfolgt.
Allgemein interessieren die als Teilmengen der Grundmenge
bildbaren Systeme, welche zumindest gebietsweise von den Normalraumwerten
abweichende Erwartungswerte der, hier als Kovariantenbildungen bezeichneten,
Grundgrößen, auch nach gewissen Zeitintervallen, erwarten lassen. Systeme
enthalten im allgemeinen Subsysteme und sind Bestandteil komplexer
Systemkonfigurationen. Dieser Anforderung genügen u.a. die durch die Dirac-Gleichung
beschriebenen Systeme, aber auch die weiterhin Kovariantenbildungen
verwendenden Gleichungen der Quantenelektrodynamik, Quantenchromodynamik,...
Diese elementaren, zumindest eine Zeit lang, stabilen Teilmengen der
Grundmenge werden Elementarteilchen genannt. Bei Weizsäcker ([W 85] S.506)
sind das statistische Verteilungen von Uren. Einzelne ebenfalls erhaltene
Eigenschaften sind die Quantenzahlen, welche durch spezielle Operationen aus
den Elementarteilchenbeschreibungen gewonnen werden können.
Zwischen verschiedenen Systemen kann es natürlich auch
eine Wechselwirkung geben. Diese wird normalerweise durch algebraische
Ausdrücke und damit gebildete Operatoren beschrieben, welche auf das
Superpositionsprinzip für lineare Ausdrücke zurückzuführen sind. Die
algebraische Verbindung verschiedener Systeme bringt so eine Mischung der
Spinor-Materie zum Ausdruck, welche als Resultierende eine Bewegungsänderung
der betroffenen Systeme oder gar eine Umwandlung beschreiben kann. In den
gängigen Theorien ist man deshalb immer bemüht, die Gleichungen zu
normieren, um die Resultate als Erwartungswerte interpretieren zu können.
Diese sind also die Erwartungswerte der Kovariantenbildungen.
Immer gelten dann die einfachen Stoßgesetze der kanonischen Mechanik bei der Annäherung zweier
Systeme, wenn die inneren, die Systeme erhaltenden, Eigenschaften stark genug
sind. Die Selbstwechselwirkung durch den Stoß der einzelnen Kugeln ist ebenso
wie in den linearen Wechselwirkungen, welche durch Superposition beschrieben
werden, vernachlässigbar, weil sie die Erwartungswerte an den
Raum-Zeit-Punkten nur unwesentlich ändert. Als Masse- Begriff kann schon hier
vorgreifend die Anzahl der beteiligten Kugeln angenommen werden.
Selbstwechselwirkung der Feldgrößen durch den Tausch
einer Komponente bei einem elementaren Zusammenstoß spielt demnach bisher
keine Rolle, obwohl gerade durch diese eine ständige Veränderung der
Feldgrößen zu erwarten wäre. Ständige chaotische Änderungen würden aber
nach der gängigen Vorstellung alle weiteren Überlegungen ad absurdum
führen. Ohne sie ist hiermit eine modellmäßige Beschreibung und damit das
Verständnis der in den modernen physikalischen Theorien vorkommenden
geometrischen Objekte, welche auf die zusammenstoßenden Uratome
zurückführbar sind, möglich. Das ist die notwendige Bedingung für die
Akzeptanz des vorgeschlagenen Weges. Als hinreichende Bedingung werden nun die
Symmetrien in der Grundmenge mit Selbstwechselwirkung untersucht, weil
landläufig angenommen wird, dass in einer Menge wirr durcheinander fliegender
stoßender Kugeln keine Symmetrien auftreten und somit keine stabilen Systeme
entstehen können.
Im derzeitigen Entwicklungsstadium des Uratom-Modells
werden nur reelle Vektor- Größen verwendet, um später leichter weitere
gegenseitige Abhängigkeiten mit in die Formeln aufnehmen zu können.
Literatur:
[F 89]
Fachlexikon ABC Physik; 2 Bde; Thun, Frankfurt/M, 1989
[S 89]
Schmutzer, E.; Grundlagen der theoretischen Physik, mit einem Grundriß der
Mathematik für Physiker; 2 Bde Mannheim, Wien, Zürich 1989
[W 85] von
Weizsäcker, C.F.; Aufbau der Physik; München, Wien 1985
Stichworte (Ende)
![]()
Wiese,
Lothar: Struktur und Dynamik der Materie im Uratom-Modell, http://uratom.keyspace.de,
Porec 2000
Uratom (Anfang)