4.1 Teilchen bilden sich bei der Expansion

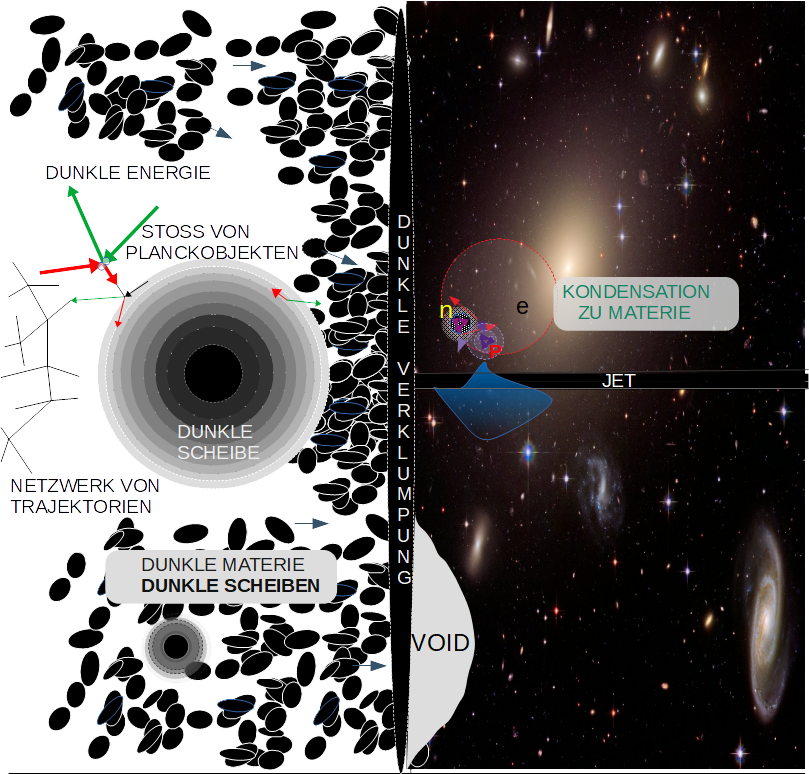
Die Scheiben haben nun innen eine hohe Dichte der kleinen Kugeln erreicht und drehen sich. Mit der Nullten Wechselwirkung kann es zur Bildung größerer scheibenförmiger Ansammlungen von Galaxien aus kalter dunkler und dann auch normaler Materie kommen. Aus den Zentren entweichen orthogonal Kugeln mit anfangs kleinen Geschwindigkeiten, also niedriger Temperatur.

Beginnend mit hoher Dichte fehlen nur in der Richtung zum Vakuum Stoßpartner. Dort entsteht eine Asymmetrie. In benachbarten Bereichen geschieht Ähnliches, mit nur kleinen Unterschieden. Stöße finden durchschnittlich nach freien Weglängen statt. Dadurch erfolgt eine schnelle Thermalisierung innerhalb des orthogonalen Strahls. Dieser weitet sich bei seiner Ausbreitung langsam auf und lässt für Raumzellen kontinuierlich Werte zu, die Mastergleichungen erfüllen. Geschwindigkeitsbetrag und freie Weglänge sind auf einer Kugel gekoppelt. Stoßpartner kommen aus verschiedenen Richtungen, welche durch die Drehung der Scheiben beeinflusst wird. Die Umgebungen von Stoßpartnern bieten so unterschiedliche Bedingungen für Strömungskeime. Bahnen von Repräsentanten erhalten durchschnittliche Öffnungswinkel bzw. Knickwinkel zwischen sich. Diese erlauben eine Schätzung der Stabilität entstehender Strukturen, welche allerdings schwer erkennbar sind. Bei 60° (bzw. ≈ 72° Raumwinkel)¹ wird diese besonders groß. Entgegen kommende Kugeln stammen aus dem Vakuum. Diese lassen sich nur mit einer notwendigen Unbestimmtheit beschreiben. Die Ecken von Trajektorien können nur stabil bleiben, wenn sie in ihrer Umgebung virtuelle Hüllen so besitzen, dass sie als Punktteilchen beschreibbar werden. Die Orte der Entstehung könnten Nullpunkte für Reservoire von MB-Verteilungen liefern. Daraus entstehen möglicherweise die merkwürdigen Eigenschaften von Quarks.

Für Animationen und zum Vergleich mit Experimenten lassen sich Simulationen verwenden. Mit der Inversionsmethode werden wenige Repräsentanten für Zustände betrachteter Strukturen erzeugt. Diese können den Eindruck kugelförmiger Teilchen erwecken. Das Ergebnis lässt nur schwer erkennen, ob sie in der definierten Menge real sein können. Auch bei heißen Strahlen aus Beschleunigern. Aus dem Randbereich könnten Teilchen verschiedener Generationen entweichen. Die Umgebung lässt Schwingungen mit unterschiedlichen freien Weglängen zu. Stabilität erfordert dabei das Hineinpassen zwischen Grenzen, welche in einem dichteren Gebiet der Entstehung mit virtuellen Hüllen vergleichbar sind. Die Idee dazu wird durch die Betrachtung des Casimir Effekts in [7], Abbildung 8.37 unterstützt.

Ins Vakuum entweichen Neutronen mit inneren Trajektorien, die bei den Knicken durchschnittlich 60° Innenwinkel bilden. Dabei treten wieder virtuelle Hüllen der Ansammlungen auf. Die freien Weglängen sind von den Geschwindigkeiten unabhängig. Stoßpartner kommen, wegen der Sprünge, aus der Umgebung. Innere Stöße würden die freien Weglängen ändern. Ladungen gibt es da noch nicht. Die Mastergleichung für ein Intervall von Ereignissen unterliegt einer Unschärfe. Im Vakuum passen Geschwindigkeiten und Orte, welche sich aus den freien Weglängen ergeben, nur ausnahmsweise dauernd für stabile Strukturen zusammen. Deshalb ist dort beispielsweise das Neutron instabil. Detaillierte Betrachtungen führen auf die bunte Evolutionsphase des Universums.

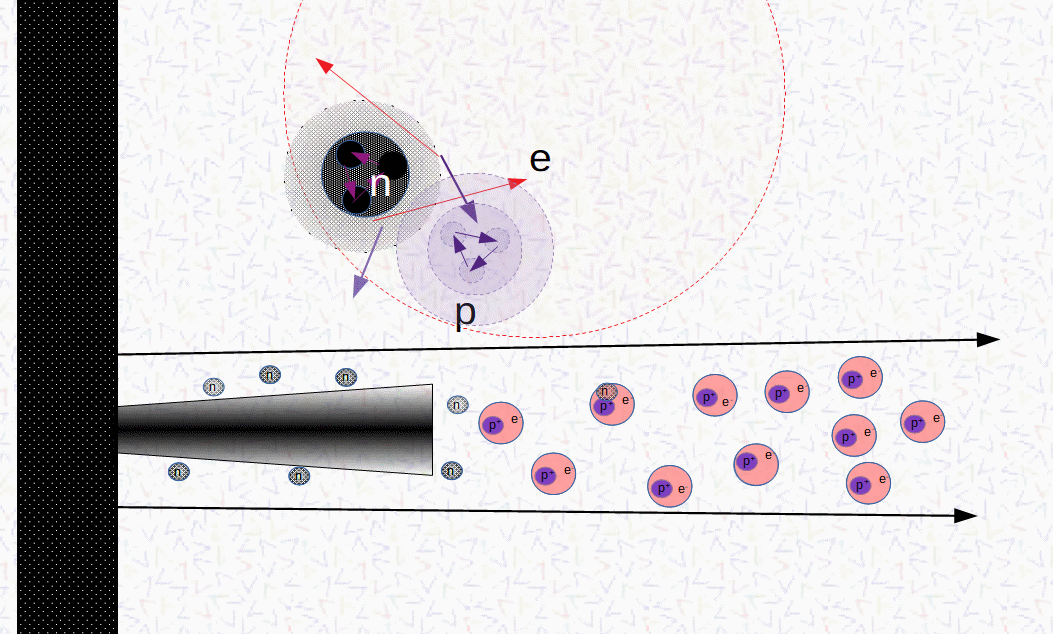
Betrachtet werden beim Zerfall von Neutronen die aus vielen Kugeln bestehen, stellvertretend zuerst zwei Repräsentanten. Ihre Darstellung kann bei der anfänglichen Beschränkung auf einen Stoß, ohne dritte Dimension, mit einer Zeichenebene auskommen (Abbildung 7). Die Nullte Wechselwirkung erzeugt spontane (abrupte) Änderungen der Geschwindigkeiten, die dadurch Änderungen von Bewegungen (dick gestrichelte Pfeile) für die Mastergleichung der Hülle (gestrichelter Kreis) des interessierenden Protons liefern. Dessen innere Relativgeschwindigkeiten sollen als radiale Geschwindigkeiten wirken. Zur kleinen Geschwindigkeit v_pr im Teilchen muss die große aus dem Vakuum v_Vakuum so passen, dass beide mit gekoppelten freien Weglängen L die gleiche für Stabilität nötige Stoßfrequenz erreichen. Der Sprung in den Bereich der Mastergleichung der virtuellen Hülle kommt zustande, weil bis dort hin kein weiterer Stoß stattfindet. Diese überwacht die Stabilität und wird in beiden Richtungen mit Frequenzen der Überquerung erfüllt. Das Gleichgewicht, welches das Massenverhältnis definiert, besitzt einen Mechanismus zur Aufrechterhaltung der Eigenschaften des Protons. Dieser hängt vermutlich mit der Thermalisierung, dem Spin 1/2, beschrieben mit Pseudovektoren und der Unschärfe im betrachteten Intervall zusammen. Die Halbwertszeit für den Zerfall von Teilchen folgt daraus und wird beim Proton und Elektron unendlich.

An einem Raumzeitpunkt kann anstelle einer konkreten Kugel die Wahrscheinlichkeit für die Geschwindigkeit und die gekoppelte freie Weglänge betrachtet werden. Das geht in die am Punkt r zum Zeitpunkt t zu erfüllende Mastergleichung ein. Dabei sind w die, wegen der Abhängigkeit von v und L, schwer mit der Inversionsmethode zu bestimmenden Übergangswahrscheinlichkeiten im betrachteten Netzwerk. Das heißt auch thermodynamisches Gleichgewicht.

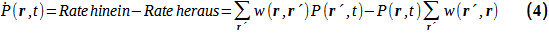
Abbildung 7: Knicke von Trajektorien zweidimensional betrachtet. Deren gekoppelte Geschwindigkeiten und freien Weglängen wirken über Relativgeschwindigkeiten mit Drehvektoren (Pseudovektoren) unter Gültigkeit von Unbestimmtheitsrelationen. Mit diesen ergeben sich Frequenzen der Überquerung von Punkten der Hülle. Aus dem Proton fluktuiert durch die virtuelle Hülle in jeder Richtung v_pr. L_pr wirkt über die Gravitation abhängig von der vorherrschenden Dichte. Von der anderen Seite kommen aus dem Vakuum v_Vakuum und L_Vakuum. Die Compton-Wellenlänge des Elektrons wird vorläufig als freie Weglänge fürs Vakuum interpretiert. Der von genialen Experimentatoren gemessene Wert hängt von der Vakuumdichte ab und beträgt nach CODATA aktuell 2.4263•10⁻¹²m. siehe auch Er bestimmt die für Stabilität notwendigen Eigenschaften von Proton und Elektron.

Am willkürlich gewählten Stoßpunkt (1) treffen zwei Kugeln aufeinander. Die Dichte ist dort größer als im Vakuum und die freien Weglängen sind entsprechend kleiner. Die Wahl von Repräsentanten zeigt nur, wie bei der Berührung Geschwindigkeitsbeträge getauscht werden. Dabei ändert sich in der Skizze die Farbe der übertragenen Komponente. Weil Geschwindigkeitsbeträge und freie Weglängen gekoppelt sind, ergeben sich neue Stoßorte. Der rot eingezeichnete nächste Stoßort liegt in einer Entfernung, welche als virtuelle Hülle vom Vakuum geprägt ist. Bis dort hin findet kein weiterer Stoß statt. (2) Entgegen kommt eine Kugel mit einem Winkel, welcher von der Relativgeschwindigkeit und vom Vakuum abhängt (3). Die Innere Geschwindigkeit und deren Richtung entsteht aus dem vorherigen Stoß (4). Die neue Richtung und Geschwindigkeit sind gekoppelt, weil sie zur gleichen Kugel gehören und werden von der Geschwindigkeit bestimmt, die freie Weglänge und der rot eingezeichnete nächste Stoßort dagegen von der inneren Eigenschaft der Ansammlung (5). Die blaue Komponente der Geschwindigkeit (6) wird in (7) zur grünen Komponente der getauschten, zum Proton gehörenden, Kugel.

Für das sich bildende Elektron ist im Gegensatz zum Vakuum ein Strömungskeim vorhanden.

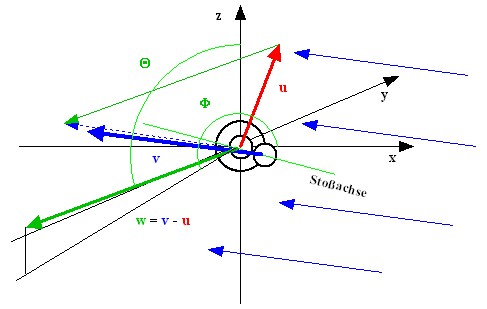
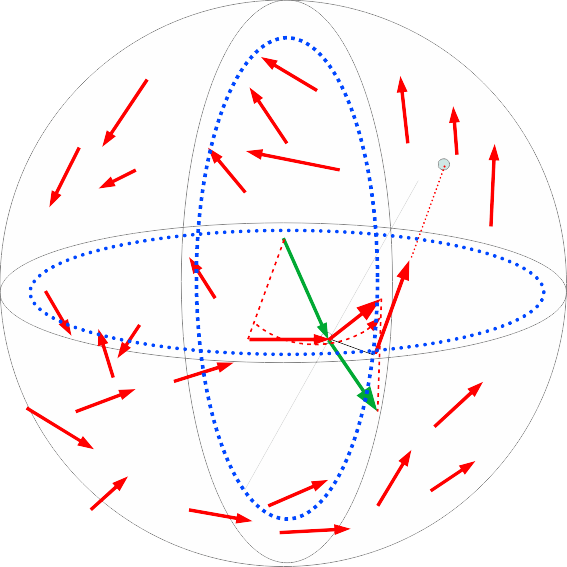
Abbildung 8: Den Spin bildet die Verteilung von Stoßachsen über Kugeloberflächen, wegen angenommener paralleler Flugbahnen. Dabei wird die dritte Dimension erschlossen.

● Von zwei Stoßpartnern integriert sich der mit dem besser passenden Winkel in eine existierende Strömung des Spins. Die freien Weglängen sind von deren Geschwindigkeiten unabhängig. ● Herrscht in der Umgebung Homogenität und Isotropie, gibt es keine Strömung, in welche sich ein Stoßpartner mischen könnte. Das ergibt den Spin Null. ● Ohne Drehachse gibt es in einer Ansammlung Strömungen rechts oder links herum. Der Zustand axialer Vektoren am unscharfen Ort von Stößen wird durch Punktspiegelungen (Drehung um 180°) beschrieben. Das ergibt den Spin ½ für betrachtete Teilchen (Abbildung 9). ● Störungen werden (fast) nicht durch Stöße beeinflusst. Ihre Frequenz und Richtung entstehen bei der Erzeugung und ergeben Wellenlängen unabhängig von den freien Weglängen des Substrats. Solche Quanten (Photonen) „sehen“ nach 360° Drehung wieder wie vorher aus. Das beschreibt der Spin 1. Die Ausbreitung mit Lichtgeschwindigkeit hängt von der Durchschnittsgeschwindigkeit / im Substrat ab.

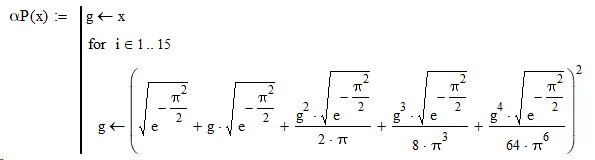
Da mit der Feinstrukturkonstante die Maxwell-Gleichungen entwickelt werden können, ergeben sich für die bunte Phase des Universums elegante Beschreibungsmöglichkeiten, auch die QED.

4.7 Nukleosynthese

Die Zukunft des Universums hängt vom Dichteparameter der Kosmologie ab. Dieser wird in 6. Resümee, [6], 12. Quantitative Zusammenhänge und hier in Gl. (3), angedacht. Wichtig ist vor allem die anfängliche Bildung von Neutronen, Protonen und Elektronen. Diese können wegen der großen Dichte zu ersten Strukturen (Atome, Moleküle,...) kondensieren. Das Verhältnis von 3/4 Wasserstoff und 1/4 Helium entsteht möglicherweise am Anfang der Expansion bei dieser kalten Nukleosynthese, im Gegensatz zur heißen Primordialen. Danach dominiert die Kernphysik, welche von der Stabilität ihrer Bestandteile abhängt. Details sind aber für das Thema nicht erforderlich.

4.8 Hintergrundstrahlung und Rekombination

Materie und Antimaterie existieren im beobachtbaren Universum nicht in gleicher Menge. Durch die Interpretation der symmetrischen Erzeugung von Teilchen aus heißen Teilchenstrahlen als einzig bekanntem Mechanismus, entsteht allerdings dieser Eindruck. In großer Entfernung wurde die Temperatur für die Hintergrundstrahlung vermutlich bei der Entstehung aus kalter dunkler Materie und deren Thermalisierung geprägt. Dabei entsteht möglicherweise keine Antimaterie, was das Koinzidenzproblem lösen würde.

Die Rekombination ohne notwendige Inflationsphase wird durch die Nukleosynthese ersetzt. Zerfallende neutrale Strukturen werden in der bunten Phase der Evolution betrachtet. Auch dort können virtuelle Hüllen zur Abgrenzung zusammen gehörender Strukturen nützlich sein. Die Rotverschiebung der Spektrallinien von Galaxien kann sowohl auf deren Alter und große Masse zurück geführt werden, als auch auf den Eindruck einer Expansion wegen der Zunahme von Leerräumen (Voids).

³ https://struktron.de/alt/2015-Feinstrukturkonstante.pdf weist auf die FSK-Iteration hin, in der gezeigt wird, dass durch mathematische Vereinfachungen physikalische Zusammenhänge verloren gehen können.