home

Szenario für ein diskretes Standard Modell auf der Basis des Massenverhältnisses 1836 vom Proton zum Elektron. Superposition von Wahrscheinlichkeiten liefert mit der Nullten WW Erklärungen für die anderen Wechselwirkungen sowie für Erscheinungen von Dunkler Materie und - Energie. Eine Beschreibung ausgehend von Abständen führt auf die Standardphysik.

2. Beschreibung von Planckobjekten (Kugeln)

Mit der begründeten Existenz sich bewegender Kugeln lassen sich Formeln für die elementare Nullte Wechselwirkung herleiten. Die mathematische Beschreibung basiert auf deren Dynamik. Die zweite Kugel erzeugt die spontane Änderung des Zustands mit Drehung der Relativgeschwindigkeit und diese ist nichtlinear. Es wird vorerst ein festes Koordinatensystem verwendet.

In der einfachen lokalen Betrachtung kommen Orte nicht vor, parallele (‖ ) und orthogonale (⊥) Komponenten tauschen:

u´(u,v,Ѳ,ф):=v_‖(u,v,Ѳ,ф)+ u_⊥(u,v,Ѳ,ф)           (1)

v´(u,v,Ѳ,ф):=u_‖(u,v,Ѳ,ф)+ v_⊥(u,v,Ѳ,ф)           (2)

Diese Kurzform von ausführlicheren Stoßtransformationen berücksichtigt nur Geschwindigkeiten in Form dreidimensionaler Vektoren u und v (fett geschrieben). Ѳ und ф sind zufällig generierte Stoßachsenwinkel, welche auf der Annahme paralleler Flugbahnen beruhen. Hinzu müssen die freien Weglängen kommen sowie die Abhängigkeit von Raum und Zeit. Axiale Vektoren helfen dann beim Verständnis.

Eine sinnvolle Beschreibung der Dynamik von Kugeln wäre mit Funktionen der vier Eigenschaften Geschwindigkeitsbetrag v, freie Weglänge L und zwei Winkel (v,L,Ѳ,ф) in Abhängigkeit von der vierdimensionalen Raumzeit (r,t) möglich. Alle können mit der Inversionsmethode (in 6. Resümee [2], erste Ansätze dafür in [1]) bei Bedarf erzeugt werden.

Abbildung 1: Einfacher Stoß zweidimensional in der Ebene der Stoßachse betrachtet. Dessen gekoppelte Geschwindigkeiten und freien Weglängen (rote Pfeile) erzeugen die nächsten Stoßorte, normalerweise in der dritten Dimension. Mit diesen ergeben sich Frequenzen der Überquerung von Punkten einer virtuellen Hülle.

Als Masse in einem begrenzten Gebiet des Substrats lässt sich die Wahrscheinlichkeit für die Anwesenheit der Kugeln interpretieren. Diese hängt vom Winkel zwischen durchschnittlichen Trajektorien ab. Dieser wird von den Geschwindigkeiten und freien Weglängen bestimmt. Änderungen von Geschwindigkeiten, werden nicht nur mit zweiten Ableitungen beschrieben. Sie lassen sich, wie in vielen Anwendungen der Physik, durch kleine Sprünge veranschaulichen. Die neu eingeführte Nullte Wechselwirkung ((1) und (2)) ergänzt Superposition und Abschneidefaktoren (Schranken) und soll einige offene Fragen beantworten. Sprünge sind schon bei der Entwicklung der Infinitesimalrechnung von Leibniz und Newton verwendet worden. Die erweiterte Forderung nach unbegrenzter Differenzierbarkeit wurde erst später eingeführt und für beobachtete Strukturen verwendet.

N Planckobjekte mit einem Index i definieren ein Netzwerk. Dieses bestimmt die Natur exakt (einschließlich der Stoßachsenwinkel), besser als jeder Rechner mit Stoßtransformationen und der Inversionsmethode (in 6. Resümee [2], erste Ansätze dafür in [1]). Hier sind die aufwändigen Ermittlungen des nächsten Stoßortes momentan nicht nötig. Mit Orten kann nun ein Netzwerk für anstehende Untersuchungen definiert werden.

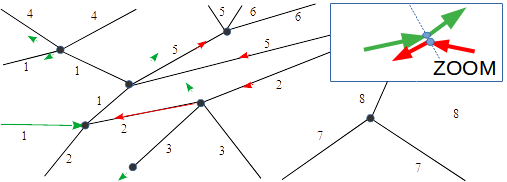
Abbildung 2: Netzwerk kausaler Trajektorien von Kugeln

Stabile Ansammlungen von Kugeln (zuerst Keime für Raumzellen) erhalten mit der Nullten Wechselwirkung virtuelle Hüllen. Diese werden durch Mastergleichungen ¹
                                                

über die Oberflächen definiert, bei denen P_k die Wahrscheinlichkeiten für einen Zustand k und T Übergangswahrscheinlichkeitsraten sind. Sie müssen gleich und anfangs würfelförmig sein, damit keine undefinierten Zwischenräume entstehen. Die Bildung arithmetischer Mittelwerte, hier einfach Durchschnitte, ergibt sich aus der Möglichkeit der Verschiebung von Vektoren.

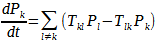
Bei jeder Kugel gekoppelte Geschwindigkeiten und freie Weglängen sowie Flugrichtungen ändern sich mit der Nullten Wechselwirkung und der neue Ort mit der gekoppelten Geschwindigkeit springt spontan. Die daraus folgende Nichtlinearität und Unschärfe kann bei großen Zahlen durch Unbestimmtheitsrelationen geglättet werden. Mit diesen kommt die Quantisierung ins Modell. Im Durchschnitt lassen sich die Bahnen vieler Kugeln durch Integrale ersetzen und es entsteht der Faktor für v_Vakuum. Bei großen Skalen ergeben sich Isotropie und Homogenität. Das Ausnutzen dieser Symmetrien führt dazu, dass Mittelwerte in Berechnungen wie Original-Werte verwendbar sind. Die große Zahl von Kugeln erschwert das Erkennen von eventuell auch fraktalen Strukturen². Diese können sich über viele Raumzellen erstrecken. Begrenzende virtuelle Hüllen haben zur Umgebung einen stabilisierenden Übergangsbereich.

Die ART betrachtet jeden Raumzeitpunkt als Ereignis. Die hiesige Beschränkung auf Berührung kleinster diskreter Objekte (Planckobjekte) als Ereignisse führt auf eine neue Definition von Zeit. Diese wird abzählbar aber wegen der großen Anzahl erscheint sie kontinuierlich. Viele Strukturen, benötigen nie Mittelpunktabstände von Null und auch in den Quantenfeldtheorien besitzen die Teilchen so viele Kugeln, dass Mittelpunktabstände nicht Null werden.

¹ Siehe unten (4), einfachere hier verwendete Einführung aus [8] Haken, Abschnitt 4.5. Siehe auch in [6] 11. Mastergleichungen bestätigen Stabilität. Diese definieren virtuelle Hüllen im diskreten Substrat.
2 Siehe z.B. https://www.youtube.com/watch?v=XSSlTr1CSg8&t=2s Fraktale im Universum.

<zurück | weiter>

Impressum  Ι  1.Einleitung 2.Beschreibung 3.Ansammlung 4.Expansion 5.Massenverhältnis 6.Resümee  Ι  alles zusammen gefasst als 1836.pdf