Ursache für Geschwindigkeitsänderungen und mit diesen für alle daraus ableitbaren physikalischen Differenziale sind nach dem hier zu entwickelnden Modell einfache spontane Geschwindigkeitsüberträge im Moment der Berührung. Nur das ist im HKM etwas Neues gegenüber der Standardphysik.

Betrachtete Grundobjekte sollen einfache bewegte feste Objekte mit spontanem Geschwindigkeitstausch bei Berührung sein. An einem Punkt des dreidimensionalen Raumes und zu einem bestimmten Zeitpunkt, können sich zwei Kugeln gerade berühren. Deshalb sollen hier der Einfachheit halber Kugeln betrachtet werden. Im deterministischen Fall werden für die Beschreibung je drei Parameter für die Geschwindigkeit benötigt. Die können beispielsweise aus zwei Winkeln und dem Geschwindigkeitsbetrag bestehen. Darüber hinaus kann die vor diesem Zeitpunkt erfolgte geradlinige Bewegung der Kugelmittelpunkte etwas versetzt gegenüber einem zentralen Stoß in Bezug auf die Relativgeschwindigkeit der beiden Stoßpartner sein. Daraus ergeben sich zwei weitere erforderliche Parameter für die auftretende Stoßachse. Hier sind demnach acht Parameter erforderlich. Die Kugelgröße hat keinen Einfluss auf die Bewegung nach dem Stoß. Erst zur Ermittlung der Häufigkeit von Stoßereignissen ist die Größe der betrachteten Grundobjekte von entscheidender Bedeutung. Sie bestimmt über die Anzahldichte die sich ergebende Stoßfrequenz. Hohe Geschwindigkeiten und niedrige Teilchenzahldichte können die gleiche Stoßhäufigkeit verursachen, wie niedrige Geschwindigkeiten mit hoher Dichte. Weil aber Objektorte und konkrete Geschwindigkeiten wegen ihrer großen Anzahl unbekannt sind, müssen für diese mindestens Anfangswerte zufällig bestimmt werden. Der Zufall kommt in das Modell, obwohl dieses deterministisch ist. Dafür sind Wahrscheinlichkeitsverteilungen erforderlich. Aus der Erfahrung mit der kinetischen Gastheorie (ideales Gas) kann man versuchsweise eine Maxwellsche Geschwindigkeitsverteilung oder eine Normalverteilung verwenden. Anstelle des einen Parameters für den Geschwindigkeitsbetrag werden nun zwei Parameter für die Durchschnittsgeschwindigkeit und die Streuung verwendet, die jeweils Funktionen der vergangenen Ereignisse sein müssen. Das Gleiche gilt auch für die (möglicherweise als gerichtet zu betrachtende, also bei bestimmten Fragestellungen nicht mehr skalare) Teilchenzahldichte und die auftretenden Winkel. Für alle gibt es Zufallseinflüsse aus der Vergangenheit und die Zahl der nötigen Parameter erhöht sich abhängig von der jeweiligen Fragestellung. Bei den molekularen Stößen auf Probeteilchen der Brownschen Bewegung werden die Teilchendurchmesser berücksichtigt. Untersuchungen durch Simulationen vieler Teilchenstöße, z.B. mit Wiener Prozessen, sind Gegenstand aktueller Forschung.

Vielfach beschreiben die Theorien der Standardphysik das Naturgeschehen, ausgehend von den kleinsten bekannten Materieportionen, also Elementarteilchen, durch Darstellungen der Poincaré-Gruppe. Je nach Interessenschwerpunkt werden dabei mehr oder weniger freie Parameter verwendet und zur Ordnung des Ganzen bieten sich beispielsweise Matrix-Darstellungen (Definition [H 90] S. 140) der den Symmetrien zugrunde liegenden Lie-Gruppen an. Für alle daraus konstruierten Feldtheorien, die in der Standardphysik verwendet werden, sind Bewegungsgleichungen erforderlich. Diese verwenden den Lagrange-Formalismus, der dann in den derzeit favorisierten Eichtheorien benötigt wird. Hier soll als Erweiterung des dabei verwendeten Begriffs von Potenzialen, welcher auf der Beschreibung durch Differenziale beruht, ein grundlegender, einfacher zu begründender, anschaulicher Vorgang, nämlich der Geschwindigkeitstausch, verwendet werden.

Zuerst werden dafür die nötigen Axiome und Definitionen angegeben, um dann zu zeigen, wie die bekannten physikalischen Gesetze in einer damit entwickelbaren Theorie verankert werden können. Alternative Betrachtungen innerhalb des Standardmodells und der ART, wie die "de-Brogli-Bohmsche Mechanik" oder die "Konsistente-Experimente-Interpretation" weisen auch auf etwas Kleineres hin, sprechen das aber nicht direkt aus. Vor allem erscheint eine spontane Geschwindigkeitsänderung in Physikerkreisen bisher wenig akzeptabel. Hier wird deshalb bewusst der Versuch unternommen, einmal auszuprobieren, was in einem einfachen HKG, entgegen aller als "sicher" geltenden Überzeugung, an Systembildungen möglich erscheint.

Axiome

Ausgangspunkt für die folgenden Überlegungen, welche die bewährten physikalischen Theorien des Standardmodells und der Allgemeinen Relativitätstheorie nicht in Zweifel stellen, ja diese sogar umfassen sollen, sind einige, möglicherweise trivial erscheinende Axiome und daraus folgende Sätze:

Axiom 1: Alles mit unseren Sinnen reproduzierbar Wahrnehmbare existiert.

Axiom 2: Zulässig (wahr) sind Beschreibungen, die A1 erfüllen.

Modelle sind vor allem dann erfolgreich, wenn sie Axiom 2 anwenden.

Beispielsweise ist das in der Standardphysik (Standardmodell ergänzt durch die ART, was hier immer angenommen wird, wenn von Standardphysik die Rede ist) der Fall. Im Verhältnis zu den vielfältigen sehr genauen Vorhersagen von Versuchsergebnissen sind die offenen Probleme klein. Diese können aber nicht verleugnet werden, was mit zur Suche nach deren Lösung, auch durch eine Erweiterung um hypothetische Objekte, beiträgt. Die "Bohmsche Mechanik" beispielsweise führt ein Führungsfeld mit verborgenen Variablen ein, die im Gegensatz zur üblichen Vorgehensweise ein Geschwindigkeitsfeld und kein Beschleunigungsfeld beschreiben. Sie kann damit einige Verständnisprobleme durch eine gewisse Anschauung lösen, wird aber gerade wegen der Nichterfüllung des Axioms 2 nicht allgemein anerkannt. In neueren Äthertheorien geht man auch von einer atomistischen Struktur aus (vgl. z.B. Schmelzer, Allgemeine Ether Theorie), es fehlt jedoch wie bei den String- oder Quantengravitationstheorien (vgl. z.B. Carlo Rovelli, Quantum Gravity) die wünschenswerte Erklärung bzw. Verringerung von ins Modell zu steckenden Naturkonstanten (c, ħ, γ, α oder Teilchenmassen) und vor allem die Begründung für die Erzeugung einer notwendigen Grundwechselwirkung. Wichtig erscheint deshalb auch noch folgendes

Axiom 3: Von allen möglichen Beschreibungen ist die einfachste die beste (Ockhams Rasiermesser).

Was als einfach angesehen wird, unterliegt aber einem zeitlichen Wandel. Früher gab es keine elektronischen Rechenhilfen, da waren analytische Methoden mit zum Teil komplizierten mathematischen Ausdrücken einfacher, als heutige massenweise Mittelwertbildungen, die zum gleichen Resultat führen, aber einfacher logisch nach zu vollziehen sind.

Axiom 4: Die Standardmodelle der Elementarteilchen und der Kosmologie (Standardphysik) liefern umfassende Beschreibungsmöglichkeiten gemäß der Axiome 1 – 3. Aus diesen lassen sich Beschreibungen und Erklärungen für die meisten Phänomene der Natur ableiten.

Es wird hier, als Beispiel für eine mögliche Beschreibung, ein Axiomensystem wie in "Ensembles" genannt, das zur "Konsistente-Experimente-Interpretation" in der Physik-FAQ von Arnold Neumaier führt. Zusammengefasst und stark vereinfacht lautet das:

Es existiert eine Menge E von Mengen, welche als Ensembles bezeichnet werden, die eine Beschreibung der uns umgebenden Realität ermöglichen.

Formal werden im Wesentlichen drei mathematische Objekte zu deren Beschreibung im Rahmen des Standardmodells festgelegt:

„1. eine fixe Algebra E von Operatoren auf einem dichten Teilraum eines universellen Hilbertraums,

2. ein selbstadjungierter universeller Hamiltonoperator H aus dieser Algebra,

3. ein normaler Zustand ρ auf dieser Algebra.

Für das reale Universum ist die Algebra E der Größen von den Feldern des Standardmodells zusammen mit der Raumzeitmetrik erzeugt, und der Hamiltonoperator der aus der zugehörigen Wirkung kanonisch hergeleitete. Der Zustand des Universums ist hingegen weitgehend unbekannt, da eine Kenntnis desselben im Rahmen der Konsistente-Experimente-Interpretation die Kenntnis aller Werte sämtlicher Felder und Korrelationsfunktionen beliebiger Ordnung an allen Orten und zu jeder Zeit impliziert. Dagegen sind die Zustände vieler Teilsysteme einigermaßen bekannt, insbesondere derer, mit denen Physiker experimentieren“ (S22. Ein Modelluniversum).

Die grundlegende Annahme der Konsistente-Experimente-Interpretation ist nun die, dass die objektiven Aspekte des Universums durch ein Ensemble (statistische Gesamtheit) in einem abstrakten Sinn gegeben sind und alles Messbare durch Erwartungswerte in diesem Universalensemble oder Funktionen von solchen Erwartungswerten (S13. Motivation für die Konsistente-Experimente-Interpretation). Die Bezeichnung E deutet auf den Begriff des Ensembles hin.

Zur Erfüllung von A1 werden physikalische Theorien so formuliert, dass sie Naturgesetze mit ihren fundamentalen Naturkonstanten als weitere Axiome enthalten. Die wichtigsten dieser Theorien werden als Standardmodell zusammengefasst. Alle anderen Naturgesetze können daraus abgeleitet werden. Der Beweis dieser Aussage ist Gegenstand der heutigen (Standard-) Physik und die obigen Axiome reichen zu deren Beschreibung vermutlich aus.

Hier soll eine Erweiterung außerhalb der Standardphysik untersucht werden, die sich allerdings der bewährten Methoden bedient. Historisch bedeutend und besonders erwähnenswert erscheinen die in der statistischen Mechanik gewonnenen Beschreibungsmöglichkeiten durch Poisson-Klammern, welche in der Quantenmechanik zu Kommutatoren bzw. Antikommutatoren führen. Von aller möglichen und üblichen Symbolik wird hier allerdings nur das benötigt, was für die angestrebte Erweiterung der Standardphysik, also nähere Untersuchungen des HKG, erforderlich ist. Dazu gehört auch etwas, was durch das Symbol ψ beschrieben werden soll, das stellvertretend für die Beschreibung freier Dirac-Spinoren oder anderer Objekte auf der niedrigsten Stufe der bisher rätselhaften kleinsten Materiekonstituenten (Elementarteilchen) stehen soll. Dieses Etwas soll in die viel kleineren Objekte, als harte Kugeln umschrieben, aufgelöst werden.

So wie Zusammenfassungen durch Mittelwert- bzw. Ensemblebildung in der Physik größere Systeme beschreiben und Messungen zugänglich machen, können zur Erklärung von Objekten des Standardmodells kleinere Objekte außerhalb dessen angenommen und möglicherweise aus den bekannten Strukturen generiert werden, was zu zeigen ist. Deshalb erfolgt hier als Arbeitshypothese ein vorübergehender Schnitt zur traditionellen Physik.

Die Motivation aus 1.3 führt zu folgendem:

Axiom 5 (Grundmengenaxiom): Es existiert einzig und allein eine Menge Ω unendlich vieler, sich im dreidimensionalen Raum bewegender fester Objekte, die hier als gleich große harte Kugeln angenommen werden. Diese durchdringen den leeren Raum gleichförmig geradlinig. Eine Annäherung an eine andere Kugel erfolgt bis zum Zusammenstoß (Berührung), bei dem nur die Geschwindigkeitskomponenten in Richtung der Stoßachse (Berührungsnormale) ausgetauscht werden.

Zur Beschreibung des HKG bieten sich verschiedene mathematische Methoden und Begriffe an. Elementar ist beispielsweise eine Zuordnung von Geschwindigkeitsvektoren zu den Kugelmittelpunkten. Damit erhalten wir 3 N Größen in einer vierdimensionalen Raumzeit, die aber durchaus noch intuitiv naiv verwendet werden kann, um Vorhersagen für die Entwicklung von Strukturen in dieser Menge machen zu können. Besonders geeignet sind die mathematischen Methoden der statistischen Mechanik bzw. der kinetischen Gastheorie für ein einfaches Gas harter Kugeln, die durch A 4 voll und ohne Einschränkung zur Verfügung gestellt werden. Verbal eignet sich dafür auch der Begriff Vakuumfluktuationen. Nachgewiesen werden soll weiter unten allerdings darüber hinaus die Verfügbarkeit einer Operation für die Beschreibung des spontanen Geschwindigkeitsübertrags durch Tausch von Geschwindigkeitskomponenten (Transposition) für die darin stattfindenden Selbstwechselwirkungen. Bisher wird dafür meist ein Potenzial verwendet, das weitere Fragen nach seiner Ursache aufwirft. Diese Operation ergänzt und erklärt demnach den wichtigsten Bestandteil des Hamiltonoperators aus Axiom 4, also die Entstehung einer Bewegungsänderung der kleinsten Objekte.

Aus Axiom 5 folgt direkt die wichtigste Forderung dieses zu entwickelnden Modells:

Alle physikalischen Systembildungen, Symmetrien, Wechselwirkungen,... und damit die Naturgesetze sind auf die Selbstwechselwirkungen, also Stöße, zurückzuführen. Bei diesen bleiben Energie und Impuls erhalten. Darüber hinaus verursachen die Ortsveränderungen der elementaren Objekte (Kugeln) die geometrisch bestimmbaren Stoßhäufigkeiten, welche ihrerseits die zweite und für unsere Umgebung wichtigere Säule, für das Hervorrufen von Geschwindigkeitsänderungen ganzer Kugelmengen (elektromagnetische Wechselwirkung <=> Stoßfrequenzänderung), darstellen. Geeignete Beschreibungen können den Methoden des Standardmodells und der ART zugeordnet werden, Grundeigenschaften des HKG können dabei allerdings verborgen bleiben.

Der Beweis des ersten Teils dieses Satzes zur Selbstorganisation, also der möglichen Beschreibung, ist leichter vorstellbar, der des zweiten Teils aber sicher sehr aufwändig und kann hier nicht erfolgen, weil das eine zu umfangreiche Aufgabe wäre.

Beweisidee für den Nachweis der Beschreibbarkeit aller physikalischen Systembildungen des Standardmodells ist, dass diese durch Mittelwert- bzw. Ensemblebildung, wie schon oben erwähnt, den Objekten unserer Umgebung zugeordnet werden können. Allen zu beschreibenden Objekten kann beispielsweise ein Phasenraum zugeordnet werden, der dann zu einem Hilbertraum erweitert wird. Mit diesem kann dann die Zuordnung zu den kleinsten Objekten, die im Standardmodell der Elementarteilchen vorkommen, erfolgen. Ohne Zweifel muss es demnach auch eine umgekehrte Zuordnungsmöglichkeit geben. Das ist nicht durch eine einfache eindeutige Abbildung möglich, aber jedem Objekt unserer täglichen Umgebung können wir zumindest gedanklich die Bestandteile, also Moleküle bzw. Atome zuordnen. Für die Generierung von Teilchenorten und Geschwindigkeiten sind Zufallsgeneratoren als Funktionen der bewährten Beschreibungen denkbar. Auf gleiche Art sollte es nun möglich sein, auch den derzeit kleinsten Strukturen des Standardmodells mit Zufallsgeneratoren noch kleinere Bestandteile, also die kleinen Kugeln oder „echten“ Atome zuzuordnen. Wichtige Voraussetzung für einen Erfolg ist dabei die Kenntnis von deren Größe, Durchschnittsgeschwindigkeit und Anzahldichte in unserer Umgebung.

Als Ansatz eines eingeschränkten Beweises soll hier gezeigt werden, dass die Differenziale der Standardphysik auf natürliche Art durch Mittelwertbildung von stoßenden kleineren Objekten erklärbar sind. Dann sollen die Möglichkeiten zur Entstehung einiger Symmetrien im HKG und die grundsätzliche Gültigkeit der wichtigsten Naturgesetze bei diesen einfachen Stößen sowie das natürliche Zustandekommen einiger Naturkonstanten gezeigt werden. Modellhaft wird das Phänomen von Anziehungs- bzw. Abstoßungseffekten im einfachen Gas harter Kugeln unter der Voraussetzung der Existenz stabiler Systeme erklärt.

Statt des Beweises für die Bildung von Elementarteilchen wird hier nur versucht, die Gültigkeit einer schwächeren Form des obigen Satzes zu zeigen:

In der durch A 5 definierten Menge können Strukturen existieren, die über längere Zeit stabil bleiben.

Auch dieser Satz widerspricht auf den ersten Blick dem zweiten Hauptsatz der Thermodynamik, deren Methoden ja gewöhnlich zur Beschreibung von Vorgängen in Gasen verwendet werden. Einen Hinweis auf stabile Strukturen geben allerdings Schallwellen, welche auch in einem einfachen Gas harter Kugeln vorkommen können. Deren Zerfließen und das Fehlen von Polarisation zerstören allerdings die denkbare Analogie zu Lichtquanten oder Elementarteilchen.

Im allgemeinen Fall müssten nun für sehr viele Objekte zu einem Zeitpunkt (Zeit muss natürlich näher definiert werden) Orte und die augenblickliche Geschwindigkeit bekannt sein. Mit solchen rein deterministischen Größen lässt sich dann prinzipiell die weitere Entwicklung des betrachteten HKG´s ermitteln. Was ist dafür erforderlich?

Definitionen für Erklärungsversuche

Zunächst wird ein Beispiel etwas näher betrachtet, um Stöße im HKG zu beschreiben. Dazu wird ein Koordinatensystem verwendet, das mit 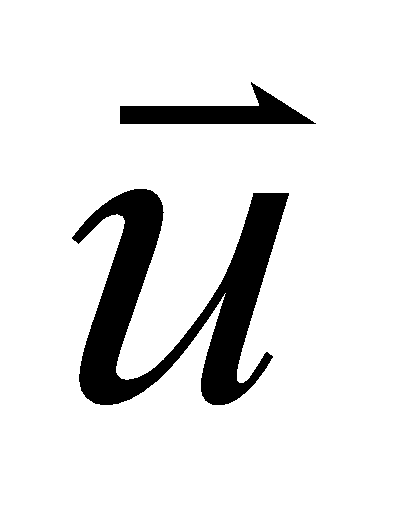in x-Richtung sowie seiner z-Richtung in der Ebene von 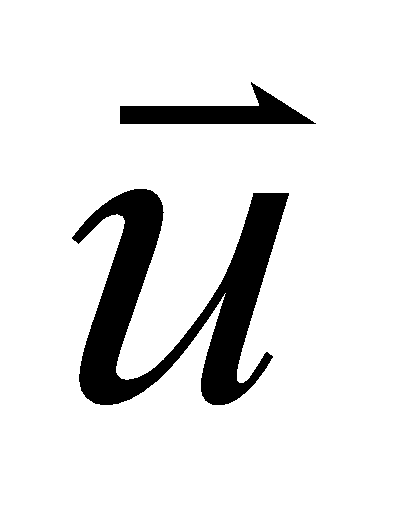und , Richtung - liegt. Zur Vereinfachung wird gemäß Abbildung 2 ein Stoßbereich mit doppeltem Durchmesser definiert, so dass in vielen Untersuchungen alle anderen Teilchen als punktförmig angenommen werden können:

d Durchmesser der stoßenden Kugeln

L (durchschnittliche) freie Weglänge bis zum nächsten Stoß

n Anzahldichte = Teilchenzahldichte (Teilchenzahl N / Volumen V) mit 0 < n < 1

wegen d > 0

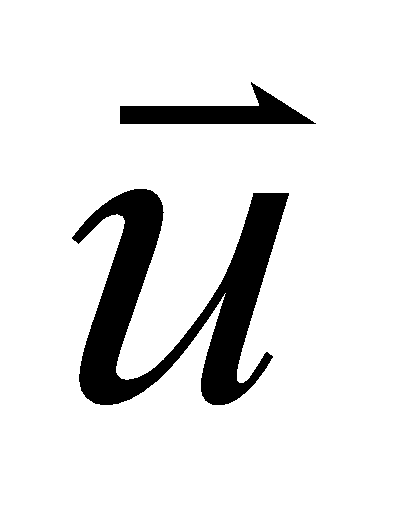Geschwindigkeit des im Ursprung startenden Teilchens

Geschwindigkeit des Stoßpartners

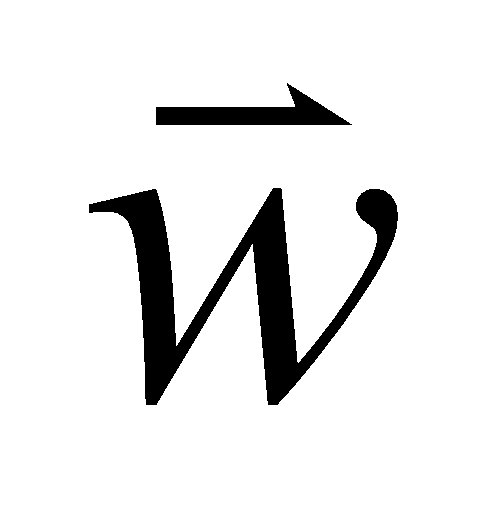Relativgeschwindigkeit -

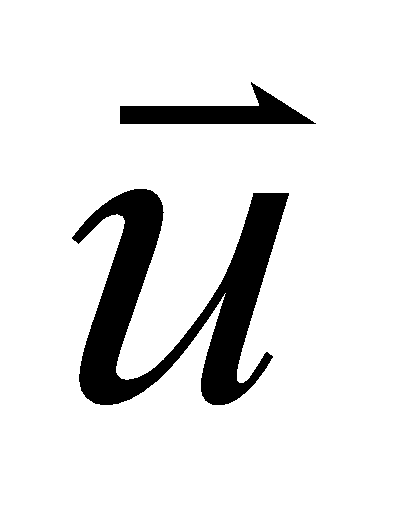
β Winkel zwischen - und 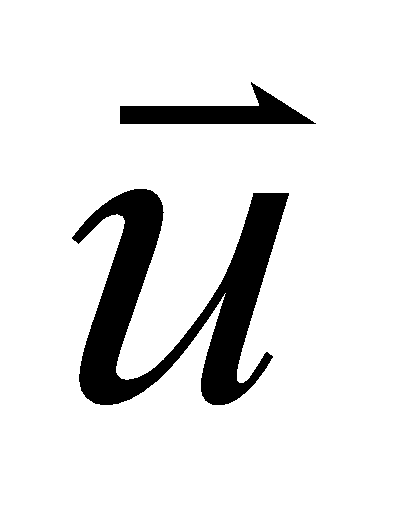, also Flugwinkel bzw. Bahnenwinkel

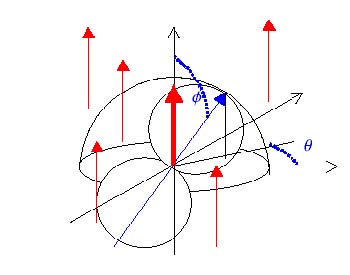
ф Herkunftswinkel der Relativgeschwindigkeit = Kollisionswinkel

Θ Drehwinkel der Relativgeschwindigkeit bzw. des Flugwinkels um ,

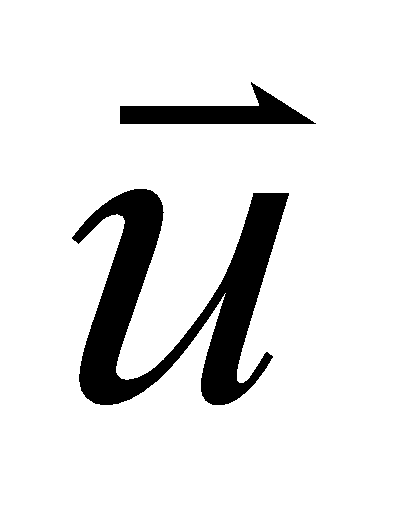verschwindet bei sinnvoller Drehung der z-Achse in Ebene mit

φ Stoßachsenwinkel (Winkel der Berührpunktnormale) erzeugt bzgl. der

Relativgeschwindigkeit, auch Streifwinkel genannt, mit -∏/2<φ<∏/2

θ Drehwinkel der Stoßachse orthogonal um Relativgeschwindigkeit

t Parameter der kontinuierlichen Zeit.

Als Vereinbarung soll darüber hinaus gelten, dass sich die Werte der obigen Winkel und Vektoren, wenn sie in Verbindung mit dem Index der Teilchennummerierung vorkommen, im Bedarfsfall auf ein festes Koordinatensystem (Laborsystem) beziehen und deshalb in dessen Werte umgerechnet werden müssen.

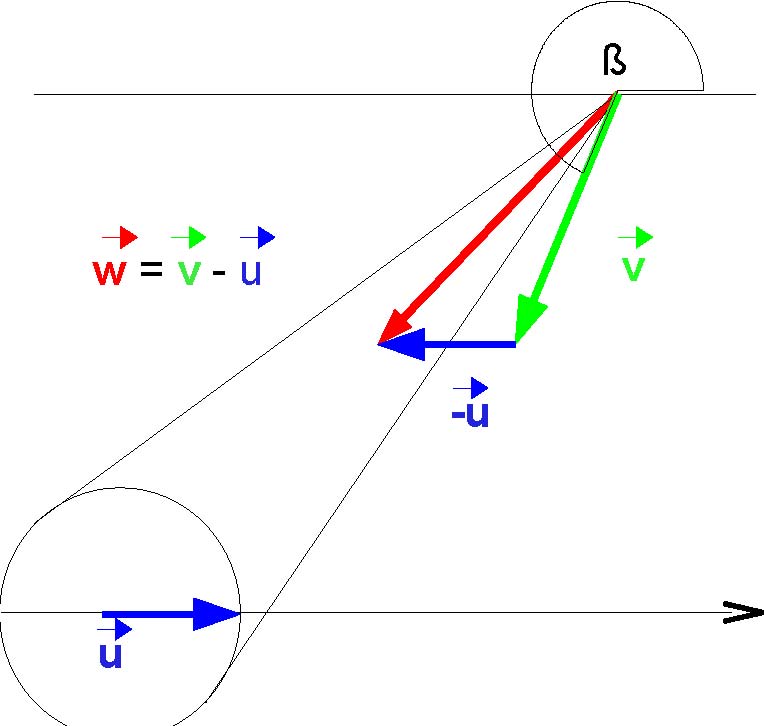
Im betrachteten harte Kugeln Gas (HKG) soll zumindest anfangs davon ausgegangen werden, dass alle N Ausgangsorte homogen im dreidimensionalen Raum, also gleich verteilt, vorkommen. Alle Flugrichtungen seien wegen der Isotropie ebenfalls gleich wahrscheinlich. Parallele Flugbahnen mit durchschnittlich gleichen Abständen voneinander sind ebenfalls zulässig (rot). Bewegte Kugeln mit festem Durchmesser d müssen zwangsweise irgendwann zu Stößen führen. Zum Zeitpunkt des gegenseitigen Berührens bildet die Relativgeschwindigkeit (dick rot) die z-Richtung eines Koordinatensystems. Relativ zu dieser ist die Stoßachse (Berührpunktnormale) auf der Kugel mit dem Durchmesser 2 d durch den Stoßachsenwinkel φ und den frei wählbaren Winkel θ definiert.

Abbildung 1: Stoßachsenwinkel

Bei Zusammenstößen ist darüber hinaus interessant, auf welche Art der Relativgeschwindigkeitsvektor 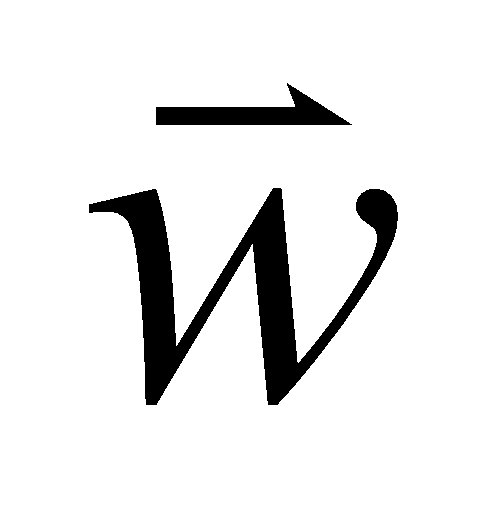gebildet wurde. Die ursprünglichen beiden Vektoren und 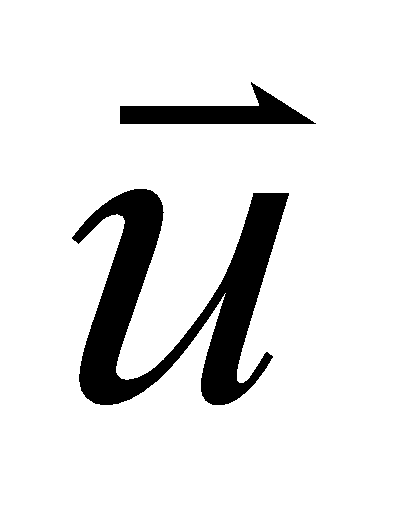können einen Winkel zueinander bilden. Dieser ist von der Bewegung des gewählten Koordinatensystems abhängig. Einer der beiden Stoßpartner (hier 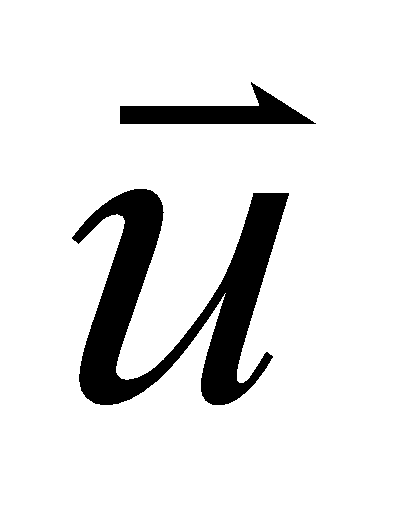) kann deshalb mit seiner Bewegung in x-Richtung gelegt werden. Bei der Bildung der Relativgeschwindigkeit bleibt diese Richtung im Laborsystem erhalten. Der Flugwinkel β (zwischen und 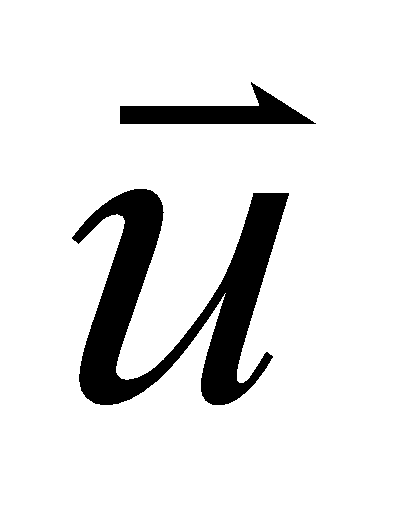) gilt wie der Winkel Ф der Relativgeschwindigkeit 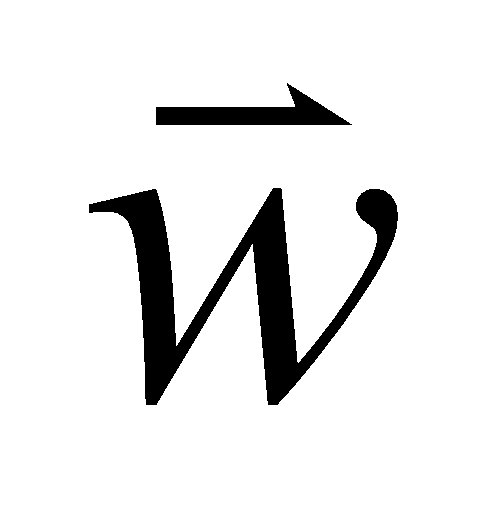im System der mit u (Geschwindigkeitsbetrag) bewegten Kugel.

Nach Abbildung 2 wird deutlich, dass es zu einem Stoß nur kommen kann, wenn der Relativgeschwindigkeitsvektor 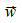in Richtung der Kugel mit dem Radius 2 d zeigt, welche mit einem gedachten ruhenden Stoßpartner gebildet und wobei die bewegte Kugel als Punkt beschrieben wird. Darüber hinaus wird von vornherein für das zu betrachtende Modell festgelegt:

Definition: Masse ist ein Maß für die beteiligte Anzahl der Kugeln. Das entspricht der Newtonschen Betrachtungsweise von Masse als Materiemenge. Den einzelnen Kugeln wird demnach eine Einheitsmasse zugeordnet.

Mit den bis hierher eingeführten Größen müssen demnach im zu entwickelnden Modell alle zur Beschreibung der beobachtbaren Phänomene verwendeten Größen abgeleitet werden können. Darüber hinaus sollten sich die Erhaltungssätze erklären lassen sowie wichtige Grundkonstanten, wie das Plancksche Wirkungsquantum und die konstante Lichtgeschwindigkeit. Für die weiteren ins Standardmodell der Elementarteilchen eingehenden Konstanten soll ein Ansatz zu deren Erklärung gesucht werden.

Abbildung 2: Stoßkegel

WEITER HKM.pdf in Deutsch