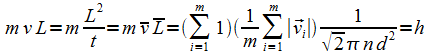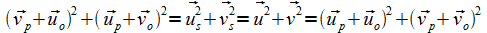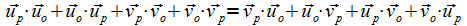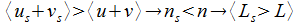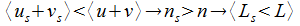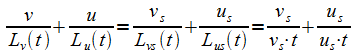Harte Kugeln Modell

"Ursache sowohl der Quantenhaftigkeit mikrophysikalischen Geschehens als auch der Gültigkeit von Unschärferelationen für die gleichzeitige Messung komplementärer physikalischer Größen ist im wesentlichen die Existenz des planckschen Wirkungsquantums h" (siehe Stichwort Quantentheorie in [M 73]). Wie ist nun diese Größe im hier betrachteten Medium zu verstehen? Das Gas muss nicht einmal unbedingt durch das Grundmengen-Axiom definiert sein. Auch kleinste Objekte, wie Strings, Branes oder sonstige Objekte mit unbekannter Struktur, wie die der Quintessenz oder des Higgs-Bosons, sind möglich. Wichtig ist nur deren geradlinige Bewegung bis zur Berührung eines anderen solchen Objektes und dann ein Geschwindigkeitstausch parallel zur Berührpunktnormale. Dieser Vorgang liegt außerhalb von Standardmodell sowie Allgemeiner Relativitätstheorie, lässt aber alle darin verwendeten Theorien unverändert in deren Gültigkeitsbereich, weil die Bewegungsgleichungen durch Stöße mit spontanem Geschwindigkeitsübertrag erklärt und hergeleitet werden können.

Eigenschaft h in der Grundmenge

Ausgehend von der Vorstellung eines gewöhnlichen Gases harter Kugeln lässt sich das HKG als Medium betrachten, welches überall vorhanden ist und die grundlegenden Eigenschaften im Mikrogeschehen unterhalb der Elementarteilchengröße beeinflusst. Aus der statistischen Physik (statistischen Thermodynamik) ist bekannt, dass sich durch Fluktuationen schnell Dichte- und Geschwindigkeitsschwankungen ausgleichen. Die Durchschnittswerte von Geschwindigkeit und Anzahldichte bleiben aber erhalten. Bekannt ist auch, dass sich mit den Größen Masse, Geschwindigkeit und (Wellen-) Länge eine neue Größe mit der Einheit einer Wirkung definieren lässt. Welche Bedeutung hat dieser Begriff nun im betrachteten HKG?

Der in die Wirkung eingehende Begriff Masse ist so grundlegend, dass er zuerst betrachtet werden soll. In der Umgangssprache und auch früher in der Physik wurde unter Masse einfach die Anzahl verstanden. Das soll hier verwendet werden. Generell bieten sich dabei zwei verschiedene Möglichkeiten an.

Erstens sind von vornherein tatsächliche Messwerte verwendbar und das Vakuum bleibt masselos, dafür besteht aber das Problem, dass die zu verwendenden Zahlenwerte nicht einzelnen Grundobjekten zugeordnet werden können, weil bei unseren heutigen Messungen die wahren Größenordnungen der Urmaterie nicht in Erscheinung treten. Diese Betrachtungsweise entspricht der, wie sie in den meisten Theorien angewandt wird, die von messbaren Phänomenen ausgehen.

Zweitens kann jedem, noch hypothetischen, elementaren Objekt die Masse 1 zugeordnet werden. Bei diesem Standpunkt muss der leere Raum, das Vakuum, auch eine gewisse Masse besitzen, die als (versteckte) dunkle Energie interpretiert werden kann. Ein gewisser Grenzbereich für darin vorkommende Systeme ist die Größenordnung der in Systemen vorkommenden freien Weglängen. Systemkugeln müssen aber nicht auf diesen Bereich beschränkt sein. Ihre Orte verschmieren bis ins Unendliche, weil Stoßgleichgewicht für den Systemerhalt mit zufälligen Stoßorten verbunden ist. Da nur Zufallswerte untersucht werden können, ist die Normalraumabweichung über den gesamten Raum, welcher sich weit vom System kaum vom Absolutwert im Vakuum unterscheidet, zur integralen Bestimmung der Systemmasse zu verwenden. Hier soll dieser neue und doch schon sehr alte Weg gegangen werden.

Deshalb gilt mit der Anzahl N gemeinsam in einem angenommenen System betrachteter Kugeln für deren Masse:

Bei der Untersuchung von Stoßfällen war eine wichtige Erkenntnis, dass sich die Geschwindigkeitsbeträge der Stoßpartner ändern. Nach einem solchen Ereignis ist ein schnelleres Objekt weiter vom Ort des Ereignisses entfernt, als ein langsames. Weitere Entfernung bedeutet eine Verringerung und eine kleinere Entfernung dementsprechend eine Vergrößerung der Teilchenzahldichte. Aus diesem Zusammenhang entsteht demnach durch die statistische Anpassung der Eigenschaften an die Umgebung eine Stabilität, das heißt ein gewisses Stoßgleichgewicht. Die Stoßfrequenz bleibt bei Betrachtung größerer statistischer Mengen unverändert, weil das Produkt aus kleiner Dichte mit hohem Geschwindigkeitsbetrag und hoher Dichte mit kleinem Geschwindigkeitsbetrag gleich bleibt. Das ist durch die Analogie zur Hydrodynamik, für die ja eine Kontinuitätsgleichung gilt, zu zeigen und führt zum Satz von Liouville. In der zur Beschreibung der Wahrscheinlichkeitsstromdichte verwendeten Stromdichte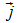

= ρ 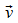, kommt die Dichte als skalare Größe vor. Thermodynamische Berechnungen verwenden, beispielsweise in den Navier-Stokes-Gleichungen, anstelle des elementareren Begriffs der Teilchenzahldichte den Begriff des Drucks, der als Impulsänderung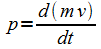

definiert ist. Die Bewährung der logischen Beschreibung durch Kontinuitätsgleichungen ist ein beobachtbares Phänomen. Mit der Anzahldichte (Teilchenzahldichte) n = N / V, dem Kugeldurchmesser d, der freien Weglänge L und der Geschwindigkeit einer Kugel

folgt dann aus der Konstanz von (30) für eine beliebige Anzahl m im Stoßgleichgewicht mit seiner Umgebung befindlicher Objekte, wie sie in stabilen Systemen, also Elementarteilchen, vorkommen sollte:

Mit der einfachen, bereits seit langer Zeit bekannten (De-Broglie-Wellenlänge, siehe unten) Beziehung wird das Phänomen formuliert. Hier werden die Größen durch solche aus der kinetischen Gastheorie ersetzt. Freie Weglängen sind zwar unabhängig von den Geschwindigkeiten, für Stabilität ist aber der wichtigere Zusammenhang für die Stoßfrequenz, also die in einem Zeitintervall zurückgelegte Strecke, von Bedeutung. Dieser Zusammenhang darf sich bei Stößen deshalb nicht ändern. Das wird nur für ein Paar zusammenstoßender Objekte gezeigt, weshalb die Masse 1 weg gelassen werden kann. Die Bezeichnungen erfolgen wie bei den Stoßtransformationen, wobei die indizierten L jetzt aber zurückgelegte Wege bedeuten und nicht von einem nächsten Stoß abhängen:

Heraus gekürzt werden können hier die konstanten Zeitfaktoren t, was bedeutet, dass nur die erreichten Orte nach einer bestimmten Zeit betrachtet werden. Damit ist das Problem auf den Fall der bei Stößen unveränderlichen Summe der Geschwindigkeitsquadrate zurück geführt (33).

Nach dem Ausmultiplizieren kürzen sich die rein quadratischen Glieder weg, so dass nur die gemischten Glieder bleiben:

Das sind aber alles Glieder, die wegen der Orthogonalität beim Skalarprodukt wegfallen, weil die Parallelität bzw. Orthogonalität sich auf die Stoßachsen bezieht. Damit ist die Behauptung bewiesen, dass bei einem Stoß die Summe der Geschwindigkeitsquadrate der beteiligten Objekte konstant bleibt, was zur Gültigkeit der Liouville-Gleichung, auch bei inneren Selbstwechselwirkungen, also Stößen, führt.

Für die Existenz der Größe h reicht die Annahme der Existenz kleinerer Objekte als sie in der Standardphysik vorkommen, die auch als verborgene Variable interpretiert werden können, mit der Wechselwirkung durch Geschwindigkeitstausch, welche die Gültigkeit der Erhaltungssätze garantiert. Deren Betrachtung, ähnlich wie in der statistischen Physik, führt dann zur konstanten Eigenschaft h, welche das gesamte Mikrogeschehen beeinflusst. Falls die einführende Behauptung (Grundmengenaxiom) als wahr akzeptiert wird, ist damit der Nachweis der Quantenhaftigkeit im HKG erbracht.

Fluktuationen

Die als Plancksches Wirkungsquantum zu interpretierende Größe h ist unabhängig von der Größe des betrachteten Systems ein Durchschnittswert. Wird ein unendlich ausgedehntes äußeres System (Universum) betrachtet, in dem andere eingebettet sind, erfolgt durch die anwendbaren Gesetze der Thermodynamik, die als effektive Theorie keine Details wie Stoßachsenwinkel oder Vektorwinkel betrachtet, durch Dichtefluktuationen normalerweise eine Anpassung der Eigenschaften. Es stellen sich schnell lokale Stoßgleichgewichte ein, was aber durch die sekundären, also erklärungsbedürftigen Kräfte beeinflusst ist. Im HKG gibt es keine Kräfte, also muss alles statistisch durch die erzeugende Geometrie und Bewegung erklärt werden.

Geometrisch hergeleitet wurden die Formeln für die freie Weglänge bzw. die Stoßhäufigkeit (vgl. (30)) und können deshalb auch im HKG verwendet werden. Die freie Weglänge ist unabhängig von der Geschwindigkeit. Nach einem einzelnen Stoß ändern sich aber die Geschwindigkeitsvektoren nach Betrag und Richtung. Ist die Betragssumme der Stoßpartner größer als vor dem Stoß, ergibt sich eine Fluktuation, ist diese kleiner, erfolgt eine Verdichtung bzw. Ansammlung der betrachteten Objekte gegenüber deren Umgebung.

Stoßgleichgewicht

Bleibt der Fluss durch eine kleine Fläche in einem größeren Zeitintervall im Durchschnitt konstant, besitzt die betrachtete Menge eine gewisse Stabilität gegenüber ihrer Umgebung. Dadurch ergibt sich in den Systemen, nach (32), weil h konstant ist, durch einfache Auflösung nach L:

was die De-Broglie-Wellenlänge bzw. Compton -Wellenlänge für alle Materie beschreibt. In den beobachtbaren Phänomenen zeigt sich diese Verknüpfung dadurch, dass kleinere Systeme (Elementarteilchen) mit größerer Masse (bzw. Energie) verbunden sind und größere Systeme mit kleinerer Masse (bzw. Energie). Für den Begriff Größe sind unterschiedliche Interpretationen möglich und auch gebräuchlich. Einerseits kann damit die tatsächliche Ausdehnung zusammen hängen, was in Streuversuchen, zumindest bei nicht perfekt kugelsymmetrischen Ansammlungen, überprüfbar ist. Andererseits kann diese als Unschärfe bei der Messung interpretiert werden. Für zusammengesetzte Systeme aus vielen Elementarteilchen ist wegen des großen eingenommenen Raumes nur diese Interpretation sinnvoll.

Gegen die alternative Interpretation einer Erzeugung des Planckschen Wirkungsquantums durch die Dynamik der Elementarteilchen selbst, also ohne kleinere Bestandteile, die auch im Vakuum vorkommen, sprechen die gleichen beobachteten Zusammenhänge bei unterschiedlichen Systemen wie Lichtquanten mit großer Wellenlänge und andererseits sehr energiereichen Makroteilchen mit kleiner Wellenlänge und ähnlichen beobachtbaren Erscheinungen (z.B. Interferenz). Die notwendige Stabilität von Systemen im betrachteten HKG, also bestimmten Elementarteilchen, wird hier nicht gezeigt. Sie könnten aus Objekten gebildet und deren innere Strukturen durch Strings, Branes, Quantenschaum oder eben auch harte Kugeln erzeugt werden und auch über längere Zeit stabil bleiben. Ein Problem bezüglich des Confinements ist dabei nicht zu erkennen, weil die geometrisch gebildeten freien Weglängen der zusammengehörenden Ansammlungen deren Ausdehnung bestimmen. Für viele normalerweise nicht stabilen Elementarteilchen folgt daraus aber als Forderung für eine Beobachtbarkeit, dass ein gewisses, wenn auch nur kurzfristiges, Stoßgleichgewicht zur Umgebung vorhanden sein muss. Das schlägt sich in einer höheren Anzahldichte und damit verbundenen, oft sehr hohen, Masse bzw. Energie nieder. Im nicht beobachtbaren virtuellen Zustand, der zur Bildung und Erklärung einer Wechselwirkung erforderlich ist, braucht die hohe Energie natürlich nicht erreicht zu sein.

Erhalt der Stoßwahrscheinlichkeit

Das Vorkommen von h kann als stärkster Einflussfaktor für den beobachteten Zufall bei Phänomenen, die durch die Quantentheorie beschrieben werden, interpretiert werden. Für einen einfachen Stoß, sind bereits acht Parameter zur Beschreibung erforderlich, deren exakte Kenntnis unmöglich ist. Aus den Eigenschaften der Umgebung können nur zufällige Werte für sie generiert werden. Trotz bewiesener Erhaltung der Geschwindigkeitsquadrats-Summe der am Stoß beteiligten Objekte ändern sich aber Geschwindigkeitsbeträge der einzelnen Objekte. Mit dieser Änderung ist gleichzeitig eine Änderung der Teilchenzahldichte verbunden, was jedoch erst bei massenweisem Vorkommen auffällt. Diese beeinflusst dann die Stoßwahrscheinlichkeit,... Wird ein festes Zeitintervall betrachtet, muss die Stoßhäufigkeit (30) bei Stößen erhalten bleiben. Das ergibt sich, wenn bei zwei Stoßpartnern die Entfernungen zu Beginn des Zeitintervalls mit der dort für den Stoßkegel (Abbildung 2), erwarteten Anzahldichte assoziiert werden. Dann lässt sich für die Stoßzahl der Quotient aus Geschwindigkeitsbetrag und freier Weglänge auf den Stoßort zu verwenden. Beim Stoß darf sich die Summe der Quotienten von beiden Teilchen nicht ändern:

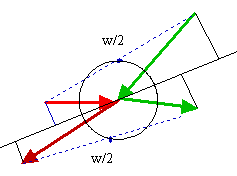
Die Relativgeschwindigkeits-Beträge bleiben nach dem Stoß gleich, obwohl die einzelnen Geschwindigkeiten stark verändert werden. Auch der mittlere Abstand der Stoßpartner ist in einem gleichgroßen Zeitintervall gleich groß wie vor dem Stoß.

Die Erzeugung unterschiedlicher Geschwindigkeitsbeträge führt zu Verzerrungen der Raumzeit durch einzelne Stöße mit der möglichen Beschreibung durch eine weiter zu entwickelnde Quantengeometrie mit deren Interpretation als statistischer Mittelwert von Stoßwahrscheinlichkeiten (Stoßfrequenzen). Das schon erwähnte Phänomen der Abhängigkeit vom Bewegungszustand, wenn man Materieportionen (Elementarteilchen) mit der Diracgleichung beschreiben möchte, führt zur Notwendigkeit, die Erzeugung der Grenzgeschwindigkeit im HKG zu zeigen.

2.5 Quantenhaftigkeit im HKM

Eigenschaft h in der Grundmenge

Fluktuationen

Stoßgleichgewicht

Bleibt der Fluss durch eine kleine Fläche in einem größeren Zeitintervall im Durchschnitt konstant, besitzt die betrachtete Menge eine gewisse Stabilität gegenüber ihrer Umgebung. Dadurch ergibt sich in den Systemen, nach (32), weil h konstant ist, durch einfache Auflösung nach L:

Erhalt der Stoßwahrscheinlichkeit