Mit den beiden letzten Kapiteln, also der Quantenhaftigkeit und der Gültigkeit der Relativitätstheorie in einem Gas kleiner Objekte, welche möglicherweise stabile Elementarteilchen bilden können, ist nun zumindest ein Rahmen abgesteckt, in dem man vielleicht einmal zu einer Allumfassenden Theorie (Theory of Everything = TOE) kommen kann. Die vorn angedeutete Möglichkeit zur Zuordnung kleinster diskreter Objekte zu den bewährten Beschreibungen der Standardphysik mit Hilfe von Zufallsgeneratoren (2.2) bildet eine Ausgangsbasis für eine große Anzahl möglicher Theorien im Rahmen des diskret erweiterten Standardmodells. Das mögliches Szenario für eine physikalisch beginnende Evolution, welches hier stichwortartig ohne Anspruch auf wissenschaftliche Untermauerung angegeben wird, erfordert vermutlich mit jeder hier durch steigende Nummern dargestellten Szene stark wachsenden Forschungsaufwand. Anfänglich in einem Gas harter Kugeln vermutete und vielleicht auch tatsächlich vorkommende Symmetrien werden dabei auf jeder höheren Stufe spontan immer weiter gebrochen (spontane Symmetriebrechung). Mit den nur angedeuteten weiteren Szenen ab Szene 9 kommen neben chemischen, biologischen, medizinischen, technischen und philosophischen Forschungen auch vielfältige Entwicklungen zu einer immer größeren Vielfalt hinzu. Durch Suchmaschinen wie Google oder lexikalische Erfassungen wie in Wikipedia wird das dabei entstehende Wissen erfasst. Ohne Anspruch auf Beweisfähigkeit wird dabei, durch die Zunahme von Strukturen, ein dem zweiten Hauptsatz der Thermodynamik entgegen gesetzter Effekt von Entropieabnahme deutlich.

3.1 Homogenes Gas

SZENE 1: Anfangs gleichmäßig verteilte, sich mit unterschiedlichen Geschwindigkeiten bewegende Kugeln stoßen ständig mit anderen zusammen. Bei den Stößen ändern sich Geschwindigkeiten und Richtungen.

Wir betrachten dazu ein HKG in sehr ferner Vergangenheit. Dichte und auch die Teilchengeschwindigkeiten seien beliebig. Stoßwahrscheinlichkeiten können bei Kenntnis lokaler Eigenschaften des HKG berechnet werden (Brendel-stoss.pdf). Querstöße kommen in diesem Gas mit größerer Häufigkeit vor, als frontale Stöße (nach B_stoss.pdf, 4.4 Abb. 8: durchschnittlich rund 72° Flugwinkel). Dabei sind nach einem seitlichen Stoß mit hoher Wahrscheinlichkeit größere Geschwindigkeitsunterschiede zu erwarten. Als Grenzwert vieler Stöße ergibt sich die Maxwell-Boltzmann-Verteilung für die Geschwindigkeitsbeträge. => Phänomene eines Gases harter Kugeln (Thermalisierung). Dabei wird immer noch die perfekte Symmetrie der vorkommenden Winkel angenommen. Das führt zur Gültigkeit des zweiten Hauptsatzes der Thermodynamik.

3.2 Evolutionsbeginn

SZENE 2: Einseitig bevorzugte Stöße erzeugen erste kleine Asymmetrie bei den Winkelwahrscheinlichkeiten. Die langsameren Kugeln bleiben länger in Nähe des Stoßortes. Erste Asymmetrien treten in dem HKG auf.

Normalerweise gibt es in keinem Raumgebiet größere Ansammlungen von Kugeln mit kleiner Geschwindigkeit. Ist allerdings genügend Zeit vorhanden, wird die Wahrscheinlichkeit groß, dass irgendwo eine solche Ansammlung entsteht, so dass in diese zufällig von außen hinein geratene langsame Teilchen nicht mehr von denen der Ansammlung unterschieden werden. Diese bleiben dann in der Ansammlung und vergrößern diese, falls von außen weiterhin Stoßgleichgewicht herrscht. Hervorrufen kann das nur eine kleine Asymmetrie bei den durchschnittlich auftretenden Flugwinkeln bzw. den damit verbundenen Stoßachsenwinkeln. Das ist nur dann der Fall, wenn die innere Geschwindigkeit entsprechend der größeren Dichte abnimmt (Phänomen Dunkle Materie) und deshalb gegenüber dem Außenbereich die Stoßfrequenzraumwinkeldichte unterschiedlich wird, also eine kleine Asymmetrie bei den Winkeln auftritt. Anfangs dürften bei diesem Effekt die Kugelgröße und die Teilchenzahldichte kaum eine Rolle spielen. Erst bei einer fast vollständigen Füllung eines solchen Bereichs werden durch die Ausdehnung der harten Kugeln die so störenden mathematischen Probleme (Divergenzen) vermieden. Dann beginnt die Bedeutung der freien Weglängen. Diese Materiesammlung widerspricht dem zweiten Hauptsatz der Thermodynamik und ist deshalb Grundlage für dessen Ergänzung, welche Systembildung durch Asymmetrie bei den vorkommenden Winkeln ermöglicht und deshalb den Beginn der Evolution zu komplizierteren zusammengesetzten Systemen erzeugt.

Außen herrschen vorerst noch fast unveränderte Bedingungen. Weil aber mehr schnelle Kugeln aus dem betrachteten Gebiet kommen und diese irgendwann außerhalb wieder mit anderen Kugeln zusammenstoßen, erhöht sich die äußere Durchschnittsgeschwindigkeit langfristig bei gleichzeitiger Abnahme der Anzahldichte (Phänomene Dunkle Energie und Vakuumfluktuationen). Dunkle Materie wird in diesem Modell demnach von langsamen, im Bezug zur Umgebung vielleicht sogar fast ruhenden kleinsten Kugeln gebildet und dunkle Energie von den sehr schnellen und im Durchschnitt immer schneller werdenden kleinsten Kugeln der Umgebung. Diese müssen auch das Medium für die Ausbreitung von Störungen und andererseits den Zusammenhalt von Systemen angesammelter kleinster Kugeln, also Elementarteilchen bilden. Dazu ist vermutlich aber noch eine allgemeine Verwirbelung durch weitere Symmetriebrüche in einer nächsten Szene erforderlich.

Quantitative Hinweise sollten sich in der zeitlichen Entwicklung des Hubble-Faktors und damit zusammenhängender Entdeckung immer fernerer Galaxien zeigen. Die Größenordnung gegenseitiger Anziehung von Sammelgebieten kann unterschiedlich von der in unserer Umgebung beobachteten Gravitation sein.

3.3 Allgemeine Drehung

SZENE 3: Gebiete mit Materiesammlung ziehen sich gegenseitig an. Dadurch kommt es zu Annäherungen und Zusammenstößen. Bei Vorbeiflügen und Zusammenstößen von Sammelgebieten erfolgen viele Einzelzusammenstöße. Eine Drehrichtung der Ansammlung ist danach bevorzugt, wenn einseitige Streifstöße häufig vorkommen (Stoßachsenwinkel -∏/2 bis ∏/2). Nun gibt es noch mehr seitliche Treffer, wodurch die einen beteiligten Stoßpartner noch langsamer werden. Es bilden sich Ströme in Drehrichtung.

Die Sammelgebiete könnten im Universum ungefähr gleichmäßig verteilt sein, so dass es wegen gegenseitiger Anziehung zu zufälligen Zusammenstößen solcher Gebiete kommt. Bei Zusammenstößen oder Vorbeiflügen von Sammelgebieten finden viele Einzelstöße statt und es wird Impuls auf das jeweils andere Sammelgebiet übertragen, der Drehbewegungen erzeugen kann. Die Vereinigung von Sammelgebieten kann zur Bildung von Vorstufen von späteren Gasansammlungen in der Form von konzentrierter dunkler Materie führen, aus der sich dann nach Einsetzen der Gravitation möglicherweise erst Kerne von Kugelsternhaufen und dann auch Galaxienkerne (schwarze Löcher) bilden könnten.

Ist nun zufällig eine Ordnung in der Art vorhanden, dass von innen nach außen die Geschwindigkeit der Kugeln zunimmt, kann durch die von außen erfolgenden Stöße ein Effekt entstehen, bei dem die Querstöße durch sehr viel schnellere Umgebungskugeln eine Richtungsänderung der Kugeln der Ansammlung verursachen, die eine Drehung der Ansammlung bedeuten. Dadurch gibt es am Ansammlungsrand sich in Drehrichtung bewegende Kugelscharen. Der Dreheffekt überträgt sich in die Umgebung durch die das Sammelgebiet verlassenden schnelleren Geschwindigkeitsvektoren, es entsteht eine allgemeine Verwirbelung der Vakuumfluktuationen. Ein mitdrehender Zeiger kann das veranschaulichen (Phänomen Nichtlokalität bzw. Verschränkung von Zuständen in einigen Experimenten). Ein quantitativ messbarer Effekt dieses Vorgangs kann mit der kleinen Asymmetrie der vorkommenden Winkel aus SZENE 2 verbunden sein und zur allgemeinen Materiesammlung führen.

3.4 Kugelansammlung (Gravitation)

SZENE 4: Eine Ansammlung leert ihre Umgebung, absorbiert demnach aus dieser Kugeln. Weil dieser Effekt zwischen mehreren Ansammlungen messbar ist, ergibt er eine Bestimmungsgröße für die Asymmetrie der durchschnittlich auftretenden Winkel und Geschwindigkeiten.

Im Sammelgebiet finden wegen höherer Dichte noch häufiger Querstöße statt. Je nach Abstand der Kugeln voneinander und dazu in Relation stehender Zahl der während der freien Bewegung von außen in das Sammelgebiet eintretenden Kugeln, kommen mehr oder weniger Stöße auf schnelle oder langsamere Kugeln vor. Diese Phase umfasst alle bekannten Wechselwirkungen, wie sie durch eine „große Vereinigung" bzw. Allumfassende Theorie (vgl. auch Hierarchieproblem) beschrieben werden sollen. Wesentlich ist das Stoßgleichgewicht zwischen Umgebungen mit unterschiedlichen Eigenschaften, das zu deren (annähernder) Stabilität führt (Phänomen Materiezusammenhalt vor allem der Teilchen mit starker WW, die aber nicht einzeln in der gesamten Ansammlung erkennbar sind). Das gesamte Sammelgebiet könnte in einem riesigen Gebiet des Universums allein vorkommen und so Vorstufe des Urknalls (Big Bang) sein oder als schwarzes Loch Vorstufe eines Gebietes zur Bildung von Kugelsternhaufen und erstes beobachtbares Anzeichen dafür könnte die Bildung von Quasaren sein. Eine Unterscheidung zwischen den beiden Modellen kann aufgrund von Beobachtungen möglich werden.

Wirr durcheinander fliegende Kugeln führen nicht zu geordneten Stößen und daher ist kein längerer Zusammenhalt zu erwarten. Genauer untersucht werden muss aber die Stoßwechselwirkung aus dem umliegenden Normalraum auf eine Schar von in Formation fliegenden Kugeln höherer Dichte. Weil große Ansammlungen angenommen werden, wird eine kleine Grenzfläche mit unterschiedlichen Eigenschaften auf beiden Seiten betrachtet, bei der aus Stabilitätsgründen durchschnittliches Stoßgleichgewicht herrscht. Äußere häufige Querstöße erzeugen hohe Geschwindigkeitsunterschiede. Langsame Kugeln bleiben etwas zurück und so wandert die Abnahme der Geschwindigkeit zum Ansammlungszentrum, weil in tieferen Schichten die langsamen auf noch langsamere treffen, für welche sie die schnelleren sind. Das kann unabhängig von möglicherweise in der Ansammlung existierenden Wirbeln (die noch keine Elementarteilchen sein müssen) erfolgen.

In den Kugelscharen kann es neben der langsamen Durchschnittsgeschwindigkeit (in möglicher Drehrichtung der Ansammlung) eine zufällige schnelle (Zitter-) Bewegung der Impulsübertragung von außen geben. Prinzipiell fliegen die Kugeln bis zu einem Zusammenstoß gerade aus. Bis zum Systemrand, d.h. der Oberfläche des Sammelgebiets, das wegen der isotropisch aus dem gesamten Raum erwarteten, außen auftreffenden Kugeln ebenfalls Kugelform haben sollte, erfolgt fast sicher einer der häufigen Querzusammenstöße. Deshalb ergibt sich vermutlich die schon in SZENE 3 beschriebene Drehung der kugelförmigen Ansammlung. Eine aus dem Außenraum mit hoher Geschwindigkeit, bevorzugt seitlich, auftreffende Kugel bleibt selbst ungefähr im Gebiet des Auftreffens, der Impuls durcheilt aber das Sammelgebiet und kann dabei immer wieder häufig seitlich auf andere Kugeln treffen. Weil diese zur Ansammlung gehören und deshalb Bestandteil von Schwärmen sind, ist deren Geschwindigkeit jeweils annähernd gleich um den in der jeweiligen Schicht vorherrschenden Mittelwert verteilt und langsam, entsprechend der durchschnittlichen Drehung des gesamten Sammelgebiets (bis auf die erwähnten möglichen zusätzlichen kleinen thermischen Schwankungen). In manchen Schichten können Bedingungen zur Erzeugung neuer Wirbel herrschen.

Bei kleiner innerer Durchschnittsgeschwindigkeit können möglicherweise keine individuellen Systeme (Elementarteilchen) vorkommen, außen (vgl. Szene 5) könnten aber wegen der leereren Umgebung solche sich drehende kleine Ansammlungen (mit Spin) das betrachtete Gebiet verlassen. Die abprallenden zweiten Stoßpartner an der Oberfläche des Sammelgebietes könnten ebenfalls eigenständige Wirbel bilden, die beispielsweise als elektromagnetische Felder interpretiert werden können. Die gesamte Ansammlung würde so zu einer Elementarteilchenquelle und vielleicht Kugelsternhaufen entstehen lassen.

Dieser Sammeleffekt könnte nun unendlich lange weiter gehen, wobei lediglich das Gebiet immer weiter wächst. Aus sehr weiten Entfernungen kommen immer neue Objekte (harte Kugeln) hinzu, deren kleinere Geschwindigkeit gut ins Sammelgebiet passt, auch wenn die Umgebung immer dünner wird, mit größer werdenden Geschwindigkeiten. Dabei gibt es aber eine Beschränkung. Die Zahl der Stöße in der Umgebung nimmt immer mehr ab, weil die freien Weglängen im dünnen Medium größer werden. So kommen nur noch Teilchen von sehr weit in das Sammelgebiet. Entstanden nun aber irgend wo weit entfernt weitere Sammelgebiete, wird der Raum dazwischen leer gefegt. Nur von außerhalb dieser Gebiete gibt es noch mehr Teilchen. Deshalb erfolgt wegen einer Art Schatteneffekt eine Anziehung der Sammelgebiete. Die Gravitation ist geboren (Phänomen allgemeine Anziehung zwischen Massen). Daraus folgt ein mechanischer Erklärungsansatz der Gravitation wie beispielsweise in den Druck- (http://de.wikipedia.org/wiki/Le-Sage-Gravitation) oder MOND-ähnlichen Gravitationstheorien (http://de.wikipedia.org/wiki/Modifizierte_Newtonsche_Dynamik).

Die Gravitationskonstante kann deshalb möglicherweise einen Ansatzpunkt zur Bestimmung eines Absorptionsfaktors und damit der Asymmetrie bei den Stoßwinkeln (SZENE 2) liefern sowie dann zusammen mit beobachtbaren freien Weglängen in Elementarteilchengrößen zur Bestimmung der Durchmesser der kleinsten Objekte des HKM´s beitragen. Das Dilemma der möglichen Größenverhältnisse wird ganz zum Schluss noch einmal angesprochen (vgl. auch Zahlenspielereien).

Eines der früheren Hauptargumente gegen die Absorption war die erforderliche starke Erwärmung, die aber, wegen der direkten möglichen Umwandlung der thermischen Energie in Elementarteilchen, entkräftet werden kann (vgl. auch Le-Sage-Gravitation).

3.5 Jetbildung

SZENE 5: Wegen der inneren maximalen Auffüllung eines großen Sammelgebietes kommt es bei äußerem weiteren Hinzukommen von Teilchen zu einer Verdrängung aus dem extrem dichten und langsameren Zentrum. Einzige mögliche Ausweichrichtung ist die Drehachse. Dort können Jets gebildet und wegen der vollkommen anderen Umgebung spontan Symmetrien der auftretenden Stoßwinkel gebrochen werden.

Im Sammelgebiet (im Universum erzeugt oder für kurze Zeit künstlich in Beschleunigern hergestellt) nimmt von außen die Geschwindigkeit nach innen ab, gleichzeitig aber auch die Dichte bis zur maximalen Auffüllung zu. Dabei kommt es oft zu kurzfristig hintereinander stattfindenden Stößen und als durchschnittliche Bewegungsfreiheit bleibt nur die in Drehrichtung. An der Mittelachse des Sammelgebiets wird die Bewegungsfreiheit am kleinsten, der Außendruck bleibt aber, so dass ein Ausweichen nach vielen Stößen nur an den Polen des Sammelgebiets mit der kleinen Durchschnittsgeschwindigkeit der Ansammlung möglich ist. An der gesamten Oberfläche des Sammelgebiets verlassen aber die Kugeln mit hoher Durchschnittsgeschwindigkeit das Gebiet. Die an den Polen heraus gedrängten Teilchenscharen haben intern natürlich auch nur geradlinige Bewegungen. Wegen der großen Dichte erfolgen häufige Zusammenstöße von außen, auch mit bereits gebildeten Wirbeln (verbunden mit elektromagnetischen Feldern) und vorwiegend quer und mit der hohen Geschwindigkeit der Umgebung. Dabei ist eine kurze interne freie Weglänge zu erwarten, nach der beim Stoß eine abrupte Richtungsänderung erfolgt. Eine spontane Trennung von Scharen mit kleinen Geschwindigkeiten von solchen mit großen, führt zur Bildung von zugehörigen Wirbeln. Die Herkunft aus sehr dichter Umgebung bevorzugt das Vorkommen dichter Systeme mit kleinerer Durchschnittsgeschwindigkeit, was wir als Bevorzugung von Materie- gegenüber Antimateriebildung interpretieren können. Die Asymmetrie zeigt sich in den die größte Masse tragenden Protonen. In laborerzeugten Jets ist diese Asymmetrie geringer und es entstehen annähernd gleich viele Teilchen wie Antiteilchen, weil die Entstehungsgebiete gleich nahe der dünneren Umgebung liegen. Eine große Vereinigung der Wechselwirkungstheorien unter Beibehaltung dieser Asymmetrie ist demnach im Labor nicht überprüfbar. Wegen des umgebenden fast leeren Raumes werden somit zusammengehörige Portionen als Elementarteilchen in den Jets abgespalten. Deren freie Weglängen werden durch die Umgebung bestimmt, in der sich ein Stoßgleichgewicht einstellt (Phänomen mit ħ quantisierte Elementarteilchen).

3.6 Elementarteilchenbildung

SZENE 6: Auf Dreiecksbahn sich bewegende Kugelscharen befinden sich mit der Umgebung im Stoßgleichgewicht, bis nicht eine entscheidende Kreuzung interner Kugelscharen dieses Gleichgewicht stört. Durch Außenstöße erfolgt eine Verwirbelung, welche die Stoßzahl von Innen verringert (=> starke Asymmetrie der vorkommenden Bahnenwinkel). Dabei werden erneut Symmetrien gebrochen, deren annähernde Beschreibung dem Standardmodell zugeordnet werden kann.

Schlüsseleffekt für die Systembildung bzw. -erhaltung ist das Verhalten beim Auftreffen auf einen Schwarm gemeinsam fliegender Kugeln aus bevorzugten Richtungen. Diese Asymmetrie bei den vorkommenden Winkeln muss im HKM die Elementarteilchen bildenden Kugelmengen zusammen halten. In einen solchen hineingeratende Objekte werden nicht mehr von denen des Schwarms unterschieden. Sie verstärken den Effekt in Richtung weiterer Ansammlung bis zur maximal möglichen durch Stoßgleichgewicht bestimmten, Auffüllung. Schnellere verlassen schneller dieses Gebiet. Schnelle Stöße von außen sind ebenfalls häufiger Querstöße. Erfolgen diese zentral, führen sie lediglich zu einem schnellen Übertrag auf eine tiefer in der Ansammlung befindliche Kugel. Bei seitlichem Stoß wird der Geschwindigkeitsunterschied groß und es erfolgt ein weiterer Sammeleffekt. An den Gebietsgrenzen kann aber ein Stoßgleichgewicht herrschen, weil wenige schnelle zur gleichen Stoßfrequenz führen können, wie viele langsame. Durch die freien Weglängen wird nun ein Gebiet aufgespannt, in dem es trotz oder gerade wegen der seitlich aus der Umgebung auftretenden Kugeln kleine Wirbel geben kann, welche in ihrer Umgebung stabil bleiben. Die kleineren oder größeren Geschwindigkeitsvektoren des Schwarms können trotz geradliniger Bewegung im Durchschnitt Wirbel bilden. In Experimenten können diese kleinen Ansammlungen mit ähnlichen kollidieren, wobei nur der Systemmittelpunkt bei der Bahnverfolgung in Erscheinung tritt. Die gesamte Schar erscheint punktförmig, weil zu jeder Kugel ein Stoßpartner da ist und die Systembewegung wegen des starken Zusammenhalts in einer vom Schwerpunkt bestimmten Richtung weiter fliegt. Größere oder kleinere das System bildende Geschwindigkeitsvektoren bestimmen wegen der gegenteiligen, das System verlassenden, Vektoren die Ladung. (Phänomen => Lepton)

Bei sehr dichten Kugelschwärmen kann es Stoßzentren geben, in denen die Kugeln bevorzugt mit solchen des betrachteten Systems zusammen treffen. Geschieht das massenweise, wird die durchschnittliche Bewegungsrichtung möglicherweise so geändert, dass der Strom eine neue Richtung erhält. Sind nun in so einem Gebiet genügend Kugeln vorhanden, die ins System passen, kann dieses stabil sein. Im anderen Fall kommt der Fluss durcheinander und das System löst sich auf. Dabei sind aber Scharen in (vermutlich gerade drei) verschiedenen Flugrichtungen vorhanden. In jedem Stoßerwartungsgebiet ist es am günstigsten, wenn für jede dort ankommende Kugel ein Stoßpartner vorhanden ist (Stoßgleichgewicht). Die Teilschwärme können nicht allein existieren, die Stabilität wird durch die freie Weglänge bestimmt (Phänomene => Confinement, Quarks und starke Wechselwirkung, siehe auch Uratommodell). Übrige verlassen das Gebiet im freien geradlinigen Flug, bis sie auf Kugeln des Vakuums (Normalraum) treffen. Die Beschreibungsunterschiede von Leptonen und Quarks durch die Symmetrien des Standardmodells werden vom Stoßgleichgewicht gegenüber der Umgebung (U(1)xSU(2)) bzw. zu systeminternen Stoßerwartungsgebieten (SU(3)) bestimmt. Höhere Dimensionen sind zur Erklärung nicht erforderlich, können aber zur mathematischen Beschreibung verwendet werden.

Ein, zwei oder drei freie Weglängen der gesammelten Kugeln könnten zusammen mit der maximalen Auffüllung des Gebietes und der Stabilität zur Umgebung die Zahl der beobachteten Elementarteilchengenerationen festlegen.

Beide stabile Kugelmengenarten, d.h. die ganz dichten Quarks bzw. die im Stoßgleichgewicht mit ihrer Umgebung, also dem Vakuum, stehenden Leptonen , haben im Durchschnitt Geschwindigkeitsbetragsüberschüsse oder -mängel (Phänomen => elektrisches Feld = Geschwindigkeitsvektoren). Auch außerhalb dieser Mengen werden dabei Kugelmengen von den Quellen zu Senken transportiert (Phänomen => Magnetfeld = Kugelmengenfluss). Neutrale zusammengesetzte Systeme emittieren weder größere noch kleinere Geschwindigkeitsvektoren, das Stoßgleichgewicht mit dem Vakuum muss bei stabilen Systemen aber trotzdem vorhanden sein. Daraus folgt, dass die systeminterne Durchschnittsgeschwindigkeit der Kugeln, die das elektromagnetische Feld bilden, wegen der höheren Dichte angesammelter Kugeln, niedriger als die Vakuumlichtgeschwindigkeit c sein muss.

3.7 Bildung von Eichbosonen (Photonen)

SZENE 7: Überschüssige von Systemen abgelöste Kugelscharen können massive Eichbosonen bilden. Fehlende, mit durchschnittlicher Normalraumgeschwindigkeit, von Kugelscharen absorbierte Teilmengen bilden Scharen, die in eine feste Richtung ins Vakuum davon eilen (Photonen). Die beteiligte Anzahl an Kugeln und deren Geschwindigkeiten ergeben das für Stabilität wichtige, aber im Raum fortschreitende Stoßgleichgewicht: Phänomen => gequantelte Energie mit c = const.

Die genauere Untersuchung von übrigen Schwärmen sollte zeigen, dass die Eigenschaften bekannten Phänomenen entsprechen. Die Anzahldichte mit der konstanten Geschwindigkeit c ergibt die bestimmte freie Weglänge einer zusammengehörigen Portion (Phänomene => Quantenhaftigkeit, De-Broglie-Wellenlänge). Würde beim Flug die ursprüngliche bei der Störung entstandene Kugelmenge über viele freie Weglängen transportiert, würden sich durch die vielen Zusammenstöße Quanten schnell auflösen. Deshalb reichen die durch massive Eichbosonen vermittelten Kräfte nicht sehr weit. Ein Stoßgleichgewicht in der offenen Umgebung ist bei den überschüssigen Kugelmengen nicht vorhanden und deshalb verursacht eine Änderung der Dichte eine Veränderung der Geschwindigkeiten und umgekehrt, weil immer Querstöße vorherrschen und die zugehörigen Kräfte, welche mit Hilfe von virtuellen Teilchen beschrieben werden, verlieren durch Thermalisierung Energie an den durchquerten Raum. Massive Eichbosonen, die nur auf linksdrehende Elementarteilchen wirken, also die schwache Wechselwirkung verursachen, besitzen diese Eigenschaft möglicherweise auch als virtuelle Teilchen mit viel weniger Masse. Das kann zur Störung und Umwandlung eines fast stabilen Systems ausreichen.

Aufgebraucht bzw. absorbiert werden Kugelmengen aus der Umgebung, wenn in dem beteiligten System eine höhere Stabilität zur Umgebung entsteht. Die Eigenschaften werden deshalb wohl durch eine Wellenbewegung weiter gereicht und treten erst bei einer Wechselwirkung mit anderen Systemen zutage (Messung). Je nach Art der Wechselwirkung wird entweder der Aspekt der Geschwindigkeit oder jener der Anzahl gemessen. Wegen des Fehlens von Stoßfrequenzraumwinkeldichte bewegen sich in den Leerraum aus der Umgebung Kugeln, weil erwartete Stoßpartner nicht ankommen. Eine solche Störung muss sich deshalb mit der konstanten Lichtgeschwindigkeit des umgebenden Raumes fortbewegen, die vom Mittelwert der Kugelbewegungen erzeugt wird. Einzelne solche Störungsquanten können sich nicht durch Thermalisierung auflösen, wie das bei massiven Quanten der Fall sein kann.

Beschrieben werden können diese als elektromagnetische Wellen zu deutenden Störungen durch die Maxwellsche Elektrodynamik oder genauer durch die Quantenelektrodynamik. Eine mögliche Zuordnung von harten Kugeln zu den wesentlichen Größen dieser Theorien mit Zufallsgeneratoren wurde schon vorn angedeutet.

Die elektrischen Feldkomponenten können mit den lokalen Durchschnittswerten der Geschwindigkeitsvektoren verknüpft werden. An einem Raumzeitpunkt müsste aber die gesamte Struktur, möglicherweise bei ganz naher Betrachtung mit fast chaotischen diskreten Geschwindigkeiten vorkommen können. Das deutet die Schwierigkeit der Beschreibung (durch eine Wellengleichung => vorn) an. Wird die Wahrscheinlichkeitsverteilung der Geschwindigkeiten betrachtet, müssen deren wichtigste Parameter zu jeder möglichen Raumrichtung angegeben werden, also mindestens der Erwartungswert und die Streuung. Das Gleiche ist dann für die Teilchenzahldichten der harten Kugeln in jeder Raumrichtung erforderlich, wobei nur die von den auf den betrachteten Raum-Zeit-Punkt zu fliegenden Kugeln erzeugten Wahrscheinlichkeitsverteilungen, welche auch zu Ereignissen, also Stößen führen können, von Bedeutung sind.

3.8 Potenzialbildung von Kugelmengen (z.B. Elektromagnetismus)

SZENE 8: Die wichtigsten Wechselwirkungen unserer direkten Umgebung werden durch Potenziale hervor gerufen. Diese sind bei ihrer Entstehung vom Durchschnittswert der Geschwindigkeitsbeträge abweichende, also asymmetrische in Elementarteilchen erzeugte, Durchschnittswerte.

Die elektroschwache Wechselwirkung ist hier in der Form von mischenden Geschwindigkeitsvektoren dargestellt. Obwohl diese eigentlich nur reine elektrische Felder (virtuelle Photonen) beschreiben, kann der Mechanismus auch auf die Kugelmengen-Flüsse (Anzahldichte) des magnetischen Feldes und beispielsweise systeminterne Axialvektorströme der schwachen Wechselwirkung angewandt werden. Diesen superponierbaren Wechselwirkungen ist im HKM gemeinsam, dass die aus anderen Systemen kommenden, sich örtlich überlagernden und mischenden Objekte, vor allem auch in ihrer allein möglichen nicht realen Beschreibung durch Wahrscheinlichkeitsfunktionen, nicht von systeminternen unterschieden werden können. Die kurzfristigen durch Außenstöße innen weitergegebenen Geschwindigkeitsvektoren bilden nicht die Masse, sondern sind eher überlagert wie die kurzfristigen Impulse bei einem Kugelstoßpendel.

Eine Verlagerung des Systems erfolgt immer dorthin, wo die zu den systeminneren Eigenschaften ähnlichste Umgebung anzutreffen ist. Erklärt wird das durch das weiter fliegen als normal erwartet und die Ununterscheidbarkeit von alten und neuen Systemkugeln. Das ist in Abbildung 11 durch die schwarzen Verbindungslinien angedeutet (vgl. auch Kapitel Elektroschwache Wechselwirkung auf Uratom.de). Nichts anderes besagt aber die Wirkung eines Potenzials auf ein System. Es besitzt die Fähigkeit, Arbeit zur Beschleunigung des Systems zu verrichten.

Für die Berechenbarkeit der auftretenden Potenziale sind möglicherweise nicht einmal grundlegende Informationen über die Kugelgrößen und die Anzahldichte erforderlich. Die Potenziale werden in den Elementarladungen erzeugt. In der hier vorgestellten Idee zur Entwicklung eines harte Kugeln Modells entsprechen den elektromagnetischen Feldern demnach Kudelmengenflüsse, welche von den normal erwarteten abweichen. Die virtuellen Verschiebungen in den Variationen zur Gewinnung der Bewegungsgleichungen im Lagrange-Formalismus der Feldtheorien werden somit etwas anschaulicher. Das notwendigerweise geltende Prinzip der stationären Wirkung charakterisiert die Stabilität der betrachteten Kugelmengensysteme (Elementarteilchen). Die unbekannten versteckten geradlinigen Bahnen (auch zu interpretieren als Bohmsche Trajektorien) der einzelnen Objekte, welche die betrachteten Systeme bilden, geben auch den in der De-Broglie-Bohm-Theorie verwendeten verborgenen Parametern eine anschauliche Bedeutung.

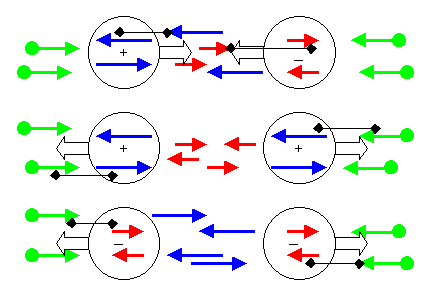
Abbildung 11: Potenzialbildung durch Mischung

Zur Überprüfung, ob in Systemen harter Kugeln, durchschnittlich Geschwindigkeitsbeträge erzeugt werden können, die innen niedrigere Durchschnittswerte und außen entsprechend höhere erzeugen oder umgekehrt, kann der Zeitfaktor und die räumliche Verteilung vernachlässigt werden, wenn man ohne diese auf die bei den Stößen durchschnittlich vorkommenden Winkel schließen kann. Diese können dann in einer Simulation vieler Stöße, ähnlich der zur Thermalisierung, verwendet werden. Dabei lässt sich möglicherweise unter vorsichtiger Betrachtung und mit einer noch nicht untermauerten Wahrscheinlichkeitsdichte für den Bahnenwinkel ß, nach vielen Stößen eine Annäherung der durchschnittlichen Geschwindigkeitsbetragsänderung an die Feinstrukturkonstante zeigen.

3.9 Ausblick auf möglicherweise im HKM erklärbare Phänomene

SZENEN 9... Stichwortartiger Hinweis auf wichtige im HKM zu lösende Probleme und dafür nötige Theorien.

Maximale Raumfüllung, dafür kein Stoßgleichgewicht mit Vakuum sondern nur mit Kugelschar aus lokaler Umgebung: Phänomen => Quarks.

Scharbewegung und Anzahl so, dass eine zusammengehörende Menge im Stoßgleichgewicht mit Vakuum: Phänomen => Lepton.
Im HKG auftretende Symmetrien => Elementarteilchentabelle.

Bei Materieansammlungen können, trotz der relativ kleinen Geschwindigkeiten durch die massenweise Geschwindigkeitsaufspaltung der Querstöße, Systeme mit gleicher Anzahl auf zwei verschiedene Arten gebildet werden, je nachdem ob als ladungsbildende innere Kugelschar die langsamen oder die schnellen gebildeten Geschwindigkeiten verwendet werden. Die jeweils anderen verlassen das System außen, zählen aber mit ihrem Feld zur Systemenergie: Phänomen => Antimaterie.

Auf dreiecksförmigen geschlossenen Bahnen sind maximal drei zusammengehörige Scharen möglich: Phänomen => drei Farben der Quantenchromodynamik.

Stoßachsenwinkel durchschnittlich 45° mit Stoßpartner aus Umgebung: Phänomen => Spin 1/2.

Unabhängiges systeminneres Stoßgleichgewicht (auch schnell bewegte Systeme): Phänomen => Spin ganzzahlig (Boson).

Van der Waals Rest der langsamen Ansammlungen interpretiert als freie Weglängen: Phänomen => starke WW.

Geschwindigkeitsunterschiede in Ansammlungen: Phänomen => el. m. WW (el. schw. WW)

Überschüsse bewegter Kugelmengen die nicht in lokale Systeme passen fliegen in Formation durchs Vakuum, bis sie gemessen werden: Phänomene => Neutrinos.
Absorbierte (fehlende) Kugelmengen ergeben Störungen welche sich mit c ausbreiten: Phänomen => Photonen.
Spins führen zu allgemeiner Raumverwirbelung: Phänomen => Nichtlokalität.

Unbekannte Sendegeschwindigkeit fernen Lichts: => c = konstant nur lokales Phänomen.

Auch mit Lichtquanten stoßen Normalraumkugeln zusammen: Phänomene => Rotverschiebung fernen Lichts.
Das Vakuum enthält thermalisierte Kugeln mit Maxwellverteilng: Teil des Phänomens => Hintergrundstrahlung.

In der Kosmologie wird die Entfernung von Objekten dadurch beschrieben, dass sich der Raum zwischen den Objekten ausdehnt <=> freie Weglängen werden zwischen den betrachteten Objekten größer <=> Kugeln werden in den Objekten (durch Gravitation) absorbiert und deshalb wird dort das HKG dünner.

Ungefähr 80% der Kugeln sind versteckt im "leeren" Raum und ihre Geschwindigkeiten nehmen zu: Phänomen => dunkle Energie.

Großer Anteil der bereits angesammelten Kugelmengen sind unsichtbar => Phänomen dunkle Materie.

In sich drehenden Sammelgebieten ist die Drehachse ausgezeichnet. Dort bilden sich möglicherweise die Elementarteilchen und treten als Jet aus. Das kann bei allen kosmischen Objekten auftreten, bei denen es nicht durch die thermische Bewegung (z.B. durch Kernfusion verursacht) wieder zerstört wird, z.B auch in braunen Zwergen: Phänomen => Jetbildung.

Größenverhältnisse im HKG für eine diskrete Erweiterung des Standardmodells

Das Problem exakter Werte für die Dichte, Geschwindigkeiten und Größen der anzunehmenden kleinen harten Kugeln muss gelöst werden. Dabei gibt es in der Anfangsüberlegung verschiedene Dilemmas der Vakuum-Raumdichte:

a) sehr dünn (L -> unendlich) => für Systeme fehlt Stoßfrequenz, kochende Vakuumfluktuationen sind kaum denkbar aber Photonen können ohne Störung den Raum durchqueren, ein kleiner Einfluss durch Stöße erzeugt Rotverschiebung und Gravitation. Schwer bzw. überhaupt nicht erklärbar wäre das Zusammenbleiben eines Photons (Portion von Kugeln) über lange Zeit, weil die erzeugenden Stöße geringfügig unterschiedliche Flugrichtungen erzeugen. => LASER wäre schwer erklärbar.

b) dünn (z.B. L -> 10 cm) => ausreichend Stoßfrequenz für Systeme, kochende Vakuumfluktuationen aber elektromagnetische Wellen werden ständig gestört bzw. der Wechsel von Schnelle und Dichte (unterhalb der Größenordnung von L im Gegensatz zu Schallwellen) muss erklärbar werden. Die Ausbreitungsrichtung (Poyntingvektor) bei den bisherigen Definitionen der elektromagnetischen Feldkomponenten stimmt nicht.

c) dichter => positive und negative Dichteabweichungen können für elektrische Ladungen verantwortlich sein. Stoßachsenwinkel in bevorzugten Außenbereichen können bei Wirbeln Zusammenhalt erzeugen. Ausbreitung elektromagnetischer Wellen könnte auf Sog beruhen. Damit könnte Polarisation erklärbar werden.

d) Photonen sind immer gleich schnell => dürften nicht durch Stöße gestört werden oder der Einfluss gleicht sich statistisch aus => Raum dürfte nicht stark gefüllt sein oder das Zerfließen wird statistisch verhindert

e) Photonen sind durch Maxwell-Gleichungen beschreibbar und haben deshalb im HKM Dünne und Dichte sowie Schnelle und Langsamkeit => Geschwindigkeit kann nur konstant sein, wenn diese Eigenschaft bei der Ausbreitung exakt symmetrisch ausgeglichen vorhanden wäre => elektromagnetische Eigenschaften treten nur bei Wechselwirkungen auf, bei der Ausbreitung muss die Eigenschaft durch die (symmetrische) Struktur der sich mit c als Durchschnittsgeschwindigkeit bewegenden Ansammlung (Photon) wellenförmig weiter getragen werden.

f) Dunkle Materie und dunkle Energie enthalten annähernd 95 % der Materie, sind aber auf viel mehr Raum verteilt als die bekannte Materie => dünner Raum.

Schreibt man die Zitterbewegungen der Elementarteilchen in der Diractheorie (vgl. S. 50 und weitere in [BD-M 90]) den Vakuumfluktuationen (vgl. auch [BD-F 90] S. 45, wo sie durch unendliche Zahl harmonischer Oszillatoren beschrieben werden) zu, sind das im HKM kurzfristig absorbierte bzw. emittierte harte Kugeln in den Kugelsystemen. Beispielsweise ergibt sich zwischen zwei Protonen für die Stärke der Gravitation die dimensionslose Zahl 5,9 · 10^-39. Die elektromagnetische Wechselwirkung ergibt die ebenfalls dimensionslose Feinstrukturkonstante ≈ 1/137. Die räumliche Symmetrie des Vakuums in allen Richtungen um eine Ansammlung (Elementarteilchen oder System vieler solcher,...), also die Isometrie, kann nur durch in der Nähe befindliche weitere Ansammlungen durcheinander gebracht werden. Aus deren Richtung wird also nicht die normal aus dem Vakuum erwartete Stoßfrequenzraumwinkeldichte vorherrschen. In der Richtung erfolgt demnach eine Beschleunigung. Für die Abschätzung von Größenordnungen können wir probehalber die Plancksche Elementarlänge als Durchmesser unserer kleinsten Objekte verwenden, also

d ≈ 1,62 ∙ 10^-35 m.
Drückt die Hintergrundstrahlung mit ihrer ungefähren durchschnittlichen Wellenlänge von 6 cm gerade die durchschnittliche freie Weglänge unserer kleinsten Objekte im Vakuum aus und nehmen wir an, dass wegen der Stabilität, z.B. des Protons, der angesammelten Systeme ein Stoßgleichgewicht zur Umgebung herrschen muss, ist die innere freie Weglänge viel kleiner als im Vakuum. Das ist natürlich mit einer viel größeren Teilchenzahldichte (Anzahldichte der kleinen Kugeln) als im Vakuum verbunden und führt wegen des Stoßgleichgewichts zu geringeren Durchschnittsgeschwindigkeiten in den Systemen. Für alle Geschwindigkeiten können wir nun für die jeweilige Umgebung eine durch Thermalisierung erzeugte Maxwellsche Geschwindigkeitsverteilung angeben. Nur der sehr kleine Anteil von Geschwindigkeiten der im Vakuum erzeugten MB-Verteilung, welcher mit der im betrachteten System erzeugten MB-Verteilung übereinstimmt, kann als systemrelevant interpretiert werden. Bei den in dichter Materie fast ruhenden Kugeln ist der Unterschied zur Lichtgeschwindigkeit so groß, dass tatsächlich nur der kleine Stärkefaktor der Gravitation (5,9 · 10^-39) zu erwarten ist. Größere innere Geschwindigkeiten erhöhen die Energie und deshalb den Anteil mit der Vakuum-MB-Verteilung übereinstimmender absorbierbarer Kugeln.

Gemäß der Idee, dass die Beschleunigungen von Systemen, wegen der Unmöglichkeit einer Unterscheidung von schon vorher zum System gehörenden und neu von außerhalb eindringenden Geschwindigkeitsvektoren, zustande kommen, kann deren Erzeugungshäufigkeit zur Abschätzung der gesuchten Größenverhältnisse verwendet werden. Das können allerdings auch gegenüber erwarteten fehlende Kugeln sein. Im Vakuum würde sich eine Stoßzahl von ≈ 7,07 ∙ 10⁹ pro Sekunde ergeben. Mit den 1,321 ∙ 10^-15 m multipliziert ergäbe das ≈ 9,34 ∙ 10^-6 m/sec, also beinahe Ruhe. Überlagerte thermische Bewegungen sind dabei nicht betrachtet. Von der Geschwindigkeit unabhängig ist dabei die freie Weglänge, die hier mit der Compton-Wellenlänge des Protons gleich gesetzt wird. Bei einem Durchmesser der Kugeln in der Größenordnung der Planckschen Elementarlänge ergibt d/L_p ≈ 10^-20. Wegen d/L_p ≈ n_p ∙ d³ wird die Anzahl der in einem Proton vorhandenen kleinsten Kugeln ungefähr 10⁸⁰. Eine einzelne Kugel hätte damit eine Masse von 1,672 ∙ 10^-27 kg / 10⁸⁰ ≈ 1,6 ∙ 10^-107 kg. Das Durcheilen bzw. die Weitergabe von äußeren, ja viel schnelleren Geschwindigkeiten kann wie bei einer in Reihe hängenden Kugelkette einfach zu etwa gleichartigem Austreten aus dem System führen. Geschwindigkeitszu- und -abnahmen können in kleinem Umfang mit den Zitterbewegungen in Verbindung gebracht werden, bei massenhaftem Auftreten aber mit den durch Spins verursachten Ladungen. Das muss natürlich den bewährten Elementarteilchentheorien (Standardmodell) zugeordnet werden. Weitere Zahlen, wie z.B. die dem Vakuum zuzuordnenden Werte lassen sich durch einfache Rechnungen ermitteln.

Alle Szenen sollten durch echte Berechnungen (Computerprogramme) nachvollzogen werden. Den unterschiedlichen Strukturen der Kugelmengenflüsse müssen die beobachteten Phänomene zugeordnet werden. Ein Hinweis auf den Nutzen des HKM´s ergibt sich durch berechenbare Zahlenverhältnisse und deren mögliche Beobachtung. Dazu können vielfältige Theorien abgeleitet werden, die sich auch falsifizieren lassen. Am notwendigsten sind dabei die Ermittlung von Größen der kleinsten Objekte und deren Verteilung im Universum bis zu minimalen Abständen (Null), die durch Beobachtungen untermauert werden müssen. In erster Linie sollte das durch die Suche nach sehr fernen Galaxien und einer Maximalenergie von Photonen erfolgen. Mit den gefestigten Werten lassen sich dann stabile Elementarteilchenstrukturen auch experimentell (LHC) untersuchen und deren Massen durch einfache Summenbildung bzw. Integration ermitteln. Die Erklärungsansätze grundlegender Vorgänge dürfen aber nicht über die Komplexität und endlose Aufgabe des Findens möglicher Strukturen im HKG hinwegtäuschen.

WEITER
HKM.pdf in Deutsch