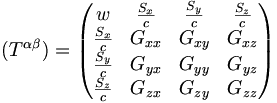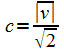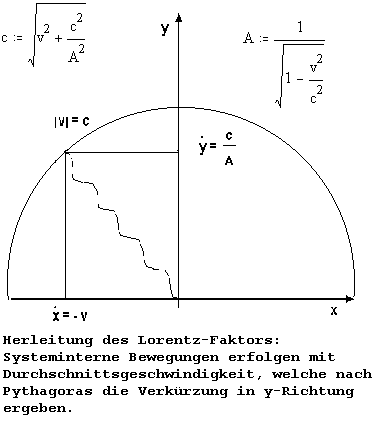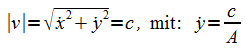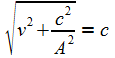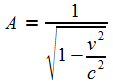Harte Kugeln Modell

Im Rahmen des HKM´s kann die Relativität nur von den Eigenschaften des HKG´s in der Umgebung aller Raumzeit Punkte wegen des Grundmengenaxioms durch Mittelwerte wie in effektiven Theorien bzw. Molekularfeldtheorien erzeugt werden. „Eins der großen Probleme des Theoriengebäudes der Physik besteht derzeit darin, dass seine beiden Säulen, die allgemeine Relativitätstheorie und die Quantenphysik, in ihrer Beziehung zueinander das Korrespondenzprinzip nicht erfüllen. Beide Theorien haben daher nur einen begrenzten Gültigkeitsbereich, so dass die heutige Physik keine abgeschlossene Beschreibung der Natur liefern kann. Es wird daher nach einer Theorie der so genannten Quantengravitation gesucht, die die Relativitätstheorie und die Quantenphysik vereinigt, indem sie beide als Grenzfall im Sinne des Korrespondenzprinzips enthält“ (aus Wikipedia: Korrespondenzprinzip, 12/2007). Das HKM erweitert die Standardphysik nur um die direkte Stoßwechselwirkung durch Geschwindigkeitstausch. Damit fallen alle Probleme der Quantenphysik und der ART in den Grenzbereichen weg, weil sich die harten Kugeln direkt berühren können, ohne dass deren Abstand der Kugelmittelpunkte Null sein kann. Die Selbstwechselwirkung (Stoß) ändert Geschwindigkeiten, die freie Bewegung ändert die Geometrie, welche zu den Stoßwahrscheinlichkeiten führt. Deshalb müssen Systeme (Elementarteilchen), welche im HKG eine Stabilität besitzen, diese durch ein Stoßgleichgewicht zum umgebenden Raum aufrecht erhalten. Unabhängig von ihrem Bewegungszustand müssen in solch ein System demnach gleich viele Kugeln aus der Umgebung hinein gelangen, wie dieses im gleichen Zeitintervall verlassen. Aus der Sicht eines solchen Systems müssen also wegen dessen Stabilität die Gesetze, welche zu dieser führen, unabhängig vom Bewegungszustand gelten. Das ist das allgemeine Relativitätsprinzip und deshalb gilt auch im HKG der Formalismus der ART.

"Die Allgemeine Relativitätstheorie ergibt sich aus dem Ansatz, die Metrik als ein Feld aufzufassen und der Forderung, dass die Wirkung invariant unter Koordinatentransformationen ist. Für diese Invarianz gibt es nicht nur ästhetische Gründe, sondern sie garantiert das Äquivalenzprinzip, dass Testteilchen bei gleichen Anfangsbedingungen gleich fallen, und ist schon in niedrigster Loopordnung für die Stimmigkeit einer Quantengravitation erforderlich." (Norbert Dragon in news:de.sci.physik am 23.01.07). Die Metrik (als Feld) wird nun im HKM von der Verteilung der bewegten Kugeln in Raum und Zeit gemäß Grundmengenaxiom bestimmt. Alle weiteren Eigenschaften der unterschiedlichsten Theorien müssen demnach ebenfalls durch Zuordnung der elementaren Eigenschaften des HKG´s beschrieben werden können. Demnach sind auch die Einstein-Hilbertschen Feldgleichungen der ART eine solche Beschreibungsmöglichkeit, die aber den anschaulichen Begriffen des HKG zugeordnet werden müssen.

Energie-Impuls-Tensor im HKG

Im Energie-Impuls-Tensor, werden die Einträge nur durch Feldeigenschaften des HKG´s bestimmt.

Bereits weiter vorn wurde erwähnt, dass Tensoren und Spinoren sowie daraus konstruierbare Felder geeignete Darstellungen der Grundgrößen von in diesem Rahmen möglichen Theorien sind. Die eingehenden Größen, wie die Energiedichte w oder die Energie-Strom-Dichten (Energiedichte mal Geschwindigkeit) S_x, S_y bzw. S_z sowie die neun G_ik des eingehenden Spannungstensors müssen natürlich als Durchschnittswerte der sich in der näheren Umgebung bewegenden Objekte ermittelt werden. Die vorn beschriebene Quantisierung mit dem Produkt aus den elementaren Größen

(32) charakterisiert das zufällige Stoßverhalten im Normalraum, zu dem stabile Systeme ein Stoßgleichgewicht besitzen müssen. Die Anzahl der an Systemen beteiligten Kugeln soll die Massen definieren und mit den Geschwindigkeiten bzw. lokalen Durchschnittswerten lassen sich lokale Energie- und Impulswerte bestimmen. Offen bleibt die Definition eines absoluten Längenmaßes für die im Energie-Impuls-Tensor notwendigen lokalen Dichten. Geeignet erscheint der unveränderbare Durchmesser d der hier angenommenen kleinsten Objekte, also harten Kugeln bzw. deren durchschnittlicher Durchmesser, falls die Objekte unterschiedlich groß wären.

Mit einer Kenntnis dieser Größen könnte nun an jedem Raum-Zeit-Punkt ein Energie-Impuls-Tensor konstruiert werden. Die vorkommenden Potenziale des enthaltenen Spannungs-Tensors G_ik können aus den räumlichen Impuls-Transporten der Umgebung, wozu auch Strahlungsfelder (was hier ebenfalls nur Kugelmengenflüsse sind) beitragen, gewonnen werden. Festgelegt ist dadurch auch die Masse stabiler Systeme und wegen des Stoßgleichgewichts mit der Umgebung die Durchschnittsgeschwindigkeit in dieser. Je nach Aufgabenstellung sollten sich daraus die an einem Raumzeit-Punkt erwarteten Stoßereignisse durch einen Zufallsgenerator ermitteln lassen. Durch die Stöße kann allerdings die raum-zeitliche Struktur der Stoßerwartungen in der Umgebung verändert werden.

Elementarste Ereignisse sind die Zusammenstöße zwischen den kleinsten Objekten. Die raum-zeitlichen Abstände zwischen solchen Elementarereignissen sind variabel und kontinuierlich, ebenso wie die diesen zugeordneten freien Weglängen oder Geschwindigkeiten. Deshalb lässt sich als Maß für das Stattfinden einer gewissen Anzahl von Elementarereignissen nur ein relatives, d.h. von den Eigenschaften des betrachteten Raumes abhängendes, Zeitmaß definieren. Je mehr elementare Ereignisse dafür einbezogen werden, desto kleiner wird die zufällige Abweichung vom Durchschnittswert der Definition.

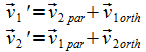
(bzw. den detaillierten Stoßtransformationen) jeder beliebige Geschwindigkeitsvektor durch einen Stoß in jeden beliebigen anderen transformiert werden. Die Erzeugung von Vektoren innerhalb bestimmter Intervallgrenzen unterliegt dabei in einem gewissen Raum-Zeit-Gebiet der Beschränkung durch die im angrenzenden Gebiet vorkommenden bzw. wahrscheinlichen Vektoren. Deshalb gilt für größere Zahlen von Stößen als Durchschnittswert die Begrenzung durch den Faktor h, wie vorn gezeigt und durch die Lichtgeschwindigkeit c, welche mit der Durchschnittsgeschwindigkeit verknüpft werden soll.

Kugelmengensysteme welche zumindest für eine gewisse Zeit stabil gegenüber ihrer Umgebung sind, müssen diese Stabilität auch in einer bestimmten Form bei einer Bewegungsänderung aufrecht erhalten. Es kann angenommen werden, dass die Stoßkomponenten in jeder Raumrichtung ausgeglichen sind. Aus vielen Kugeln bestehende Systeme, wie z.B. Elementarteilchen, behalten demnach bei einer kontinuierlichen Beschleunigung ihre Haupteigenschaften. Daraus folgt das Trägheitsgesetz und der Trägheitstensor lässt sich als Durchschnittswert durch Summenbildung ermitteln. Die Bewegungsgröße bleibt erhalten. Änderungen im Zustand des betrachteten Systems erfolgen natürlich nur bei Beschleunigung.

Wird zu jeder einzelnen Kugel eines solchen Systems rein theoretisch die gleiche Geschwindigkeitskomponente addiert, z.B. durch gleichartige Stöße auf alle, verändert sich gegenüber der Umgebung das erwartete Stoßverhalten, also die Stoßhäufigkeit und damit ändern sich auch die auftretenden Winkel. Das kann zu einer Störung der Stabilität des Systems führen. Falls jedoch die systemerhaltenden Größen stärker sind als eine infinitesimale Änderung der Systembewegung z.B. durch Ersetzen von kleinsten Kugeln, welche eine ähnliche, aber eben doch andere Bewegungsgröße besitzen, ändert das ganze System seine Bewegung geringfügig. Verallgemeinert führt dieser Gedanke bei den noch zu behandelnden Wechselwirkungen zur Idee einer Bewegungsänderung von Systemen durch Aufsammlung von Geschwindigkeitsvektoren und dabei zur Äquivalenz von träger und schwerer Masse. Dazu gehört auch eine anschauliche Erklärung der Gravitation, welche durch die Verzerrung der Raumzeit mit den Einstein-Hilbertschen Feldgleichungen beschrieben wird. Zufällig in der weiteren Umgebung erzeugte Geschwindigkeitsvektoren, die ins System passen, können nicht von systeminternen unterschieden werden und ändern deshalb dessen Energie und Impuls. In der Umgebung aus der Richtung anderer Ansammlungen dadurch fehlende Geschwindigkeitskomponenten erzeugen einen als Gravitation interpretierbaren Sog.

Konstante Signalgeschwindigkeit

Eine Energie- bzw. Massenportion ist mit einer Ansammlung von kleinsten Kugeln verbunden, welche um den Bewegungsschwerpunkt stabil, aber dabei mit durchaus möglicher Eigendynamik (z.B. auch Drehung), verteilt ist. Bei gleichförmig bewegtem System treten mit zunehmender Geschwindigkeit immer mehr Frontalstöße auf. Die Stoßfrequenz von vorn erhöht sich. Weil ein stabiles System (Elementarteilchen, auch Photon) dabei stabil bleibt, durcheilen die frontal auftreffenden Kugeln aber das System ohne Wirkung auf dieses. Wie das im Detail passiert, kann erst mit der Struktur der Elementarteilchen bzw. von großen Kugelansammlungen untersucht werden. Einleuchtend ist aber die Symmetrie der bei den Stößen auftretenden Winkel.

In Systemen können trotz häufiger Querstöße alle möglichen Geschwindigkeitskomponenten vorkommen. Nur in Bruchteilen des durch h festgelegten Raum-Zeit-Intervalls für die Beobachtung eines Systems sind auch Überlichtgeschwindigkeiten möglich, aber diese sind nicht messbar. Die konstante Ausbreitungsgeschwindigkeit einer gewöhnlichen Störung, ergibt sich als Projektion auf eine gewählte Raumrichtung aus der Durchschnittsgeschwindigkeit der kleinsten Objekte, mit dem Erwartungswert der auftretenden Stoßachsenwinkel von 45°, bei denen es ja eine 90° Drehung der Bewegungsrichtung gibt, wegen der deshalb durchschnittlich zurückgelegten Wege einfach geometrisch zu

Dieser Wert ergibt sich übrigens annähernd auch als Schallgeschwindigkeit in Wasserstoff im Verhältnis zur gemessenen Durchschnittsgeschwindigkeit der Moleküle.

Die Konstanz der Lichtgeschwindigkeit c zwischen beliebig gleichförmig bewegten Systemen ist eine der Grundfesten der Relativitätstheorie. Stabile Systeme befinden sich in Stoßgleichgewicht mit der Umgebung. Auch für beschleunigte Systeme gilt das, was einem freiem Fall entspricht. Um welche Quelle bzw. Art der Erzeugung einer Beschleunigung es sich handelt, ist dabei unwichtig. Stabilität bedeutet, dass es zu allen zum System gehörenden Kugeln solche Stoßpartner gibt, dass deren Durchschnittsbewegung auch nach zufälligen Stößen erhalten bleibt, auch relativ zur jeweiligen Umgebung. Im bewegten System ändern sich dadurch auch die Maßstäbe, mit welchen die Bewegung gemessen werden sollte. Es kann keine absolute Bewegung festgestellt werden. Die Relativbewegung zu einem anderen System wird allerdings auch mit diesen Maßstäben gemessen und diese sind so verändert, dass genau das gleiche Ergebnis heraus kommt, wie vom anderen System aus. Die systeminneren Vorgänge, welche dazu führen, sollen wegen der gewünschten Anschaulichkeit etwas näher betrachtet werden.

Im HKG ist es möglich, mit Nicht-Durchschnitts-Geschwindigkeiten, Änderungen im Bewegungsablauf eines stabilen Systems (Elementarteilchen) hervorzurufen. Das kann im Wesentlichen, nach den bisherigen Überlegungen, ausschließlich durch Mischung von Kugelströmungen oder direkte Stöße erfolgen. Über größere Abstände der Systeme sind solche Ströme als Störungen im Normalraum nur mit den darin herrschenden Geschwindigkeiten möglich. Auch Informationen können deshalb nur mit diesen übertragen werden. Ganzen Ensembles von stabilen Systemen, die sich wiederum in einem stabilen Stoßgleichgewicht zueinander befinden, kann auch eine gemeinsame Bewegung überlagert sein. Wegen des Stoßgleichgewichts, das die Stabilität gegenüber der Umgebung gewährleistet, kann die Eigenbewegung gegenüber dem Medium (HKG) nicht festgestellt werden, zum Ausgleich von Stoßfrequenzänderungen in Bewegungsrichtung muss aber die in allen Richtungen dazu gegenüber dem HKG in Erscheinung tretende Stoßhäufigkeit durch Dichteänderungen angepasst werden.

Es wird ein (hypothetisch existierendes) stabiles System und dessen Bewegung gegenüber dem HKG des Vakuums betrachtet. Abbildung 10 zeigt eine Bewegung mit dem Geschwindigkeitsbetrag v in – x-Richtung als Änderung des Ortes, d.h. Ableitung, des in einer sinnvoll gewählten Zeiteinheit zurückgelegten Weges. Mit der Zunahme der Systemgeschwindigkeit verlagert sich der Ereignisvektor auf dem Einheitskreis in Richtung x-Achse, da die Ereigniszahl wegen der angenommenen Stabilität des Systems gegenüber der Umgebung konstant sein muss, werden immer mehr Stöße durch Frontalstöße ersetzt (die einfache Herleitung stammt aus [WS 82], S. 42).

Es gilt also wegen der möglichen Aufspaltung der konstanten systeminternen Durchschnittsgeschwindigkeit in Achsenrichtung

Das eine stabile System kann nun zu einem Ensemble gehören und von einem anderen aus, das sich in einem anderen Ensemble befindet und mit diesem eine Relativbewegung zum ersten durchführt, betrachtet werden. In jedem dieser Systeme gilt, dass die Bewegung gegenüber dem Medium, also dem HKG nicht festgestellt werden kann, weil die Stoßhäufigkeit der Umgebung angepasst ist. Andernfalls würden sich die Systeme durch die Dichtefluktuationen nach den Gesetzen der Thermodynamik schnell auflösen. Einer willkürlichen elementar mathematischen Addition von zwei Systemgeschwindigkeiten kann somit keine physikalische Erscheinung entsprechen. Die Summe muss zumindest bei der Beteiligung von zwei Systemen, welche aus vielen Objekten bestehen, eine Zahl kleiner als c sein, falls die Beobachtung in einem größeren Raumzeit-Intervall erfolgt, was ja durch die Normalraumeigenschaft h verlangt wird. Das ist die Aussage des Additionstheorems der Geschwindigkeiten der (speziellen) Relativitätstheorie. Es gilt also zwischen den relativ zueinander bewegten Systemen das (spezielle) Relativitätsprinzip und Signale können von einem Ensemble auf das andere höchstens mit der konstanten Geschwindigkeit c übertragen werden. Somit gilt der gesamte Formalismus der speziellen Relativitätstheorie auch im betrachteten Gas harter Kugeln. Dessen Herleitung braucht hier nicht wiederholt zu werden.

Die Gültigkeit ähnlicher Überlegungen für reale Gase scheitert an der Instabilität von Systemen (z.B. Gaswirbeln), wohl wegen der Asymmetrien bei den vorkommenden Winkeln. Durch die unmögliche einseitige Abschirmung von Stößen wegen der fast leeren zusammengesetzten Systeme (Moleküle), gibt es vermutlich keine einseitig bevorzugten Treffer auf diese. Schwierig wäre auch die Realisation einer Messung von Schallsignalen zwischen solchen Systemen sowie deren Bezug auf die freien Weglängen, die ja bekanntlich beim Schall sehr viel kleiner sind als die Schallwellenlängen. Trotzdem könnte aber auch ein Michelson-Morley-Experiment mit Schall durchgeführt werden.

Die Zeit wird durch die Anzahl der Elementarereignisse bestimmt. Bei einem bewegten System treten mit höherer Geschwindigkeit immer mehr Frontalstöße auf, so dass für orthogonal dazu stattfindende Stöße weniger Partner bleiben und deshalb die Zeit gedehnt erscheint. Von einem ruhenden Beobachter aus ist demnach eine Zeitdehnung bzw. Längenverkürzung oder ein Massenzuwachs anzunehmen, der mit mehr beteiligten Kugeln wegen dem notwendigen Stoßgleichgewicht verbunden zu sein scheint. Das erzeugt unter anderem auch den tatsächlich beobachtbaren relativistischen Dopplereffekt muss aber, wie noch gezeigt werden muss, nicht unbedingt Ursache der Hubble-Konstante sein.

Das Relativitätsprinzip, welches die Gleichwertigkeit der Bezugssysteme für die Darstellung der physikalischen Gesetze bestimmt und der Lorentz-Faktor sind die Basis für die (vorerst spezielle) Relativitätstheorie und die Ursache der Anwendbarkeit der Lorentz- bzw. Poincare-Gruppe. Sie gelten nach dem Obigen wegen der elementaren Raumeigenschaft h und dem damit zusammenhängenden Stoßgleichgewicht stabiler Systeme zu deren Umgebung. Viererschreibweise,..., welche das gesamte Gebäude der Theorie bilden, ergeben sich dann als rein mathematische Hilfsmittel. Der ganze Vorgang entspricht unter Einschluss der Elementarzeiten zwischen Elementarereignissen somit einer Art Diskretisierung aber nicht Quantisierung von Raum und Zeit mit Hilfe der elementaren Eigenschaften der Grundmenge wie im vorigen Kapitel. Speziell die freie Weglänge L führt bei Anwendung des rationalen Maßeinheitensystems mit c = ħ =L = 1 dazu, dass die Einheiten von

die Dimension einer reziproken Länge erhalten und die Zeit x₀ = t die einer Länge. Damit steht der Formalismus der Quantenfeldtheorie (vgl. z.B. Einführung von [B 84]) zur Verfügung.

Weiterhin gilt die herkömmliche Energiedefinition. Der relativistische Massenzuwachs gemäß m = m₀ / A ist wegen der Systembeschleunigung durch Einmischung entsprechender kleinster Kugeln und dem bei jeder Geschwindigkeit herrschenden, für Stabilität notwendigen, Stoßgleichgewicht gegenüber der Umgebung, mit einer Anzahlerhöhung verbunden. Angenommen wird, dass die Aufsammlung bzw. Einmischung von Geschwindigkeitsvektoren eine allgemeine Eigenschaft zur Beschleunigung von durch Selbstorganisation gebildeten Systemen ist. In einer Gravitationstheorie sollte das ebenfalls verwendet werden. Zufällig in der Umgebung gebildete ins System passende Vektoren könnten durch dieses absorbiert werden und dadurch einen Schatteneffekt erzeugen. Über die Teilchenzahldichte der im Vakuum vorhandenen Kugeln wird hier noch keine Aussage gemacht, nur die Eigenschaften h und c = const. sind von Bedeutung. Eine Quantisierung der Gravitation ist aber ebenso unsinnig, wie die Quantisierung der Bewegung von Kugel-Systemen, weil einzelne Kugeln (oder die allgemeineren Objekte) kontinuierlich alle möglichen Geschwindigkeitsbeträge annehmen können.

Grenzen der Gültigkeit und damit der Übergang zur Galilei-Gruppe sind somit nicht nur für Relativgeschwindigkeiten von Systemen nahe Null erklärt, sondern auch bei Verlassen der statistischen Betrachtung einer Vielzahl kleinster Objekte, welche sich im Gleichgewicht mit dem umliegenden Raum befinden und messbar sind. Unterhalb des durch die Eigenschaft h bestimmten Messbarkeitsbereichs gelten die einfachen Stoßgesetze der Galilei-Gruppe, wie sie durch die Stoßformeln definiert werden. Vor der Behandlung der Gravitation und damit der vollen Erschließung der Struktur von Raum und Zeit, muss aber noch die wichtige Mikrostruktur der Urmaterieportionen erschlossen werden. Das ist leider sehr aufwändig. Durch Simulationen oder exakte mathematische Verfahren muss eine zufällige Bildung von Elementarteilchen in Mengen stoßender Kugeln gesucht werden. Gefundenen Strukturen müssen dann die gebräuchlichen Beschreibungen der Standardphysik zugeordnet und die elementaren Vorgänge bei den Wechselwirkungen nochmals behandelt werden. Das ist eine riesige Aufgabe, die wegen unendlich vieler möglicher zusammengesetzter Strukturbildungen endlos sein wird. Erster Schritt sollte der Nachweis einer Möglichkeit zur Systembildung bzw. Entropieabnahme sein.

Mit den beiden letzten Kapiteln, also der Quantenhaftigkeit und der Gültigkeit der Relativitätstheorie in einem Gas kleiner Objekte, welche möglicherweise stabile Elementarteilchen bilden können, haben wir eine erweiterte Standardphysik mit der Möglichkeit, physikalische Phänomene mathematisch zu beschreiben sowie uns auch ein anschauliches Bild von den komplizierten Vorgängen, durch Zuordnung harter Objekte, machen zu können. ist nun zumindest ein Rahmen abgesteckt, in dem man vielleicht einmal zu einer Allumfassenden Theorie (Theory of Everything = TOE) kommen kann.

2.6 Relativität von Raum und Zeit

Energie-Impuls-Tensor im HKG

Konstante Signalgeschwindigkeit