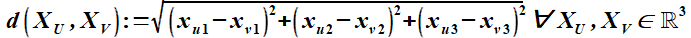	Postulierte Planckobjekte mit Ausdehnung der Plancklänge erklären durch deren Dynamik alle Kräfte. Zur Superposition von Aufenthaltswahrscheinlichkeiten kommt ein Geschwindigkeitstausch in Richtung der Stoßachsen bei Berührung hinzu. Diese nullte Wechselwirkung erklärt die Korrespondenz von Differenzialen zu realen Vorgängen. Dunkle Materie Scheiben und Dunkle Energie entstehen als erste emergente Strukturen im betrachteten Substrat. Aus Materiekeimen von Verklumpungen kondensiert die beobachtbare Materie. Seit der Berechnung der Plancklänge existiert vermutlich der Ansatz für eine Quantentheorie der Gravitation.	Grundidee: Physikalische Felder werden aus Planckobjekten (Uratomen) gebildet.
vorheriges Uratom	Die Entwicklung des Universums untersuchen auch der Excellence Cluster Universe bzw. Origins	DOM
Welche Kriterien führen zur Akzeptanz eines neuen Ansatzes? Bessere Ergebnisse als andere Alternativen.	95 % des Universums sind unerklärt (Dunkel), 95% der Menschen glauben, dass es Unerklärbares gibt. Ziel ist die Verringerung des Unerklärten.	WIKIPEDIA kann zu einer Allumfassenden Theorie (AUT) werden.
eigene Rechenwege zur FSK	Eigene alte Dokumente auf dem Weg dahin	localisator.com

Diskret formulierte Standardphysik

Erzeugung von Dunkler Materie und Energie (.pdf des ersten Ansatzes)

Diskret formulierte Standardphysik

1. Existenz bewegter diskreter Objekte (Uratome in der Größenordnung der Plancklänge, verhindern Singularitäten)

2. Orte und Zeitpunkte von Ereignissen (erzeugen die Möglichkeit von Superpositionen)

3. Stoßtransformationen (erzeugen durch Selbstwechselwirkung im Substrat wichtige Symmetrien)

4. Gültigkeit von Erhaltungssätzen (für Energie und Impulse entstehen einfach nach dem Satz von Pythagoras)

5. Erzeugung von Geschwindigkeits-Verteilungen (Maxwell-Boltzmann-Verteilung entsteht durch Thermalisierung)

6. Verteilung der freien Weglängen (sind unabhängig von Geschwindigkeiten und regeln die Wahrscheinlichkeit für Ereignisse)

7. Materie-Ansammlung (Verklumpung) (1.Anfangs-Mechanismus von Strukturbildung mit Mastergleichung 2.Bildung von Asymmetrie 3.Gravitations-Mechanismus)

8. Emission in die Umgebung (Dunkle Energie)
(Bildung von Leerräumen mit Vergrößerung durchschnittlicher freier Weglängen)

9. Erste Strukturbildung durch Materieansammlung (Dunkle Materie)
(Gravitation mit Verkleinerung der freien Weglängen durch maximale Aufenthaltsdauer zweier Uratome in der Nähe zueinander.)

10. maximale Verklumpung (dichte Kugelpackung)

bis hierher DUNKEL

ab hier BUNT

11. Jetbildung - Kondensation zu Materie
(Strukturbildung im Kleinen)

Diskretes Standard Modell (älteres .pdf)

12. Kondensation zu Elementarteilchen (freie Weglängen, Drehimpuls und Spin, Leptonen und Quarks (Spin 1/2 Fermionen), Bosonen, Hierarchieproblem)

Die hier zur Beschreibung erforderliche Quanten Chromo Dynamik ist vermutlich schon ein Hinweis auf Emergenz und Holografisches Prinzip

13. Nullte Wechselwirkung führt zu Deltafunktionen

14. Stöße erzeugen die Feinstrukturkonstante

15. Elektrische und magnetische Eigenschaften

16. Raumzeit und Gravitation (Rotverschiebung und Äquivalenzprinzip)

17. Quantenhaftigkeit
(Wirkung, Unbestimmtheit, Stabilität)

18. Quantitative Zusammenhänge

19. Holografische Strukturbeschreibung

20. Resümee

21. Ausblick

22. Literatur

23. Anhang (Definitionen, ausführliche Stoßtransformationen)

Entwurf der Zusammenfassung dieser Themen im

SM.pdf

Wichtig erscheint demnächst:

- der Versuch zur Berechnung gravitativer Anziehung zwischen Scheiben Dunkler Materie

- die Berechnung einer Funktion zur Beschreibung von Strukturen bei der Strahlaufweitung (Kondensation von Elementarteilchen)

2. Orte und Zeitpunkte von Ereignissen

Einzelne Werte für die primäre Beschreibung der Uratome eines solchen Substrats lassen sich willkürlich mit einem Zufallsgenerator (Inversionsmethode) aus verallgemeinerten inversen Verteilungsfunktionen erzeugen. Die Aufsummierung erzeugt umgekehrt das Superpositionsprinzip der Standardphysik. Zu jeder einzelnen Kugel gehören:

ein Geschwindigkeitsbetrag v,
eine freie Weglänge seit dem letzten Stoß L (alternativ zur Anzahldichte),
der Herkunftswinkel ф in der x-y-Ebene und
der Herkunftswinkel Θ in der y-z-Ebene sowie
der Zeitpunkt der zählbaren Ereignisse (Stöße) t
die Ortskoordinaten x₁, x₂ und x₃ oder
alternativ in Kugelkoordinaten ein Abstand vom Koordinatenmittelpunkt und die Winkel in der x-y-Ebene sowie in der y-z-Ebene

Mit dem euklidischen Abstand, welcher eine Metrik definiert und der aus dem Satz von Pythagoras folgt, lässt sich dann von allen betrachteten Uratomen das

	(1)

Paar auswählen, bei welchem als nächstes der Abstand 2 r (doppelter Radius) wird. Dafür gibt es geeignete Algorithmen¹, welche allerdings momentan hier nicht benötigt werden. Mit dem Index der Durchnummerierung gibt es zehn unabhängige reelle Parameter zu jedem Uratom. Für den bewährten Lagrange-Formalismus ergibt sich die kinetische Energie aus vielen Geschwindigkeiten und die potentielle mit freien Weglängen. Auch die Berührpunkte auf den Kugeloberflächen lassen sich damit exakt ausrechnen.

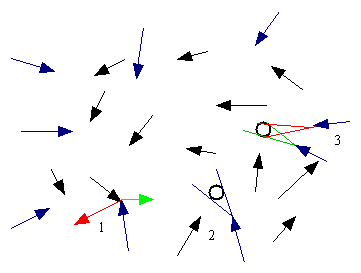
Grundmenge

Abbildung 1: Grundmenge (1 Stoß, 2 Vorbeiflug, 3 Treffer)

Sich berührende Pfeilspitzen zeigen den Ort des Stoßes.

Alle sekundären und weiteren Beschreibungen im Rahmen des Postulats müssen eineindeutige Zuordnungen zu elementaren, also primären Ereignissen zulassen. Deren sehr große Anzahl und eine Korrespondenz zur Standardphysik, empfehlen die Erzeugung zufälliger Werte der unabhängigen Parameter mit der Inversionsmethode². Die eigentliche Ereignisauswahl kann dann mit der Häufigkeit interessierender Stoßzylinder im Verhältnis zu allen möglichen, also Wahrscheinlichkeiten, bestimmt werden. Die zwei freien Weglängen L_i, die sich auch zufällig generieren lassen, liefern zwei zusätzliche Eigenschaften für die lokale Anzahldichte. Ein Stoßzylinder mit einer freien Weglänge setzt bereits zwei stoßende Uratome voraus. Bei deren Beschreibung mit Zufallsgrößen werden interessierende Intervalle für die einzelnen Parameter ins Verhältnis zu allen möglichen gesetzt.
Für einen bestimmten Stoßzylinder, dessen Inhalt proportional zu d und L oder n d³ ist, können zu einem Ereignis passende Uratome bestimmt werden. Auch dafür sind Stöße verantwortlich. Deren Häufigkeit ergibt demnach, mit dem festen d² und dem variablen L² unter Berücksichtigung der mit zwei Parametern beschriebenen Richtung, ein Maß für die zugehörige Superposition. Absorption und Emission aus lokalen Bereichen deuten schon hier auf eine Beschreibungsmöglichkeit mit der Allgemeinen Relativitätstheorie hin. Allerdings noch ohne nichtlineare Selbstwechselwirkung.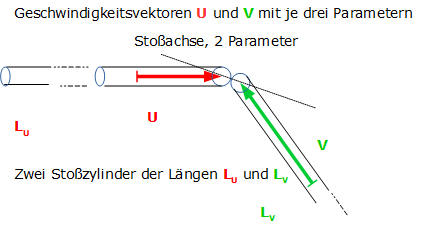

Abbildung 2: Stoßgeometrie zur Ereignisauswahl

Bei jeder Berührung von zwei Uratomen kann bestimmt werden, was dabei passiert. Eine sehr große Anzahl (Masse) verlangt Methoden zur Zusammenfassung wesentlicher Merkmale. Die Strukturen ergeben effektive Felder der Standardphysik. Aus den Eigenschaften des Substrats der Umgebung entstehen konkrete Stoßgebilde, welche in Stoßtransformationen eingehen und die Veränderungen im ganz Kleinen beschreiben (Nullte Wechselwirkung).

¹Vgl. z.B. [L 2006]

²Vgl. z.B. in [Kol 2008] Teil II – Erzeugung von Zufallszahlen und den eigenen Überlegungen für Simulationen zu „Thermalisierung.pdf“ [Wie 2009] und „Erzeugen Stöße die Feinstrukturkonstante.pdf“ [Wie 2015].

index < weiter>

Stichworte des älteren Uratom-Modells

Wiese, Albert Lothar: Struktur und Dynamik der Materie im Uratom-Modell, Porec/ Sarajevo 2000-2018