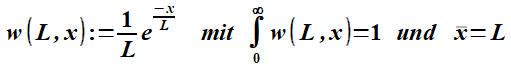Diskret formulierte Standardphysik
Erzeugung von Dunkler Materie und Energie (.pdf des ersten Ansatzes)Diskret formulierte
Standardphysik 1.
Existenz bewegter diskreter Objekte (Uratome in
der Größenordnung der Plancklänge, verhindern
Singularitäten)
2. Orte und Zeitpunkte von Ereignissen (erzeugen die Möglichkeit von Superpositionen) 3. Stoßtransformationen (erzeugen durch Selbstwechselwirkung im Substrat wichtige Symmetrien) 4. Gültigkeit von Erhaltungssätzen (für Energie und Impulse entstehen einfach nach dem Satz von Pythagoras) 5. Erzeugung von Geschwindigkeits-Verteilungen (Maxwell-Boltzmann-Verteilung entsteht durch Thermalisierung) 6. Verteilung der freien Weglängen (sind unabhängig von Geschwindigkeiten und regeln die Wahrscheinlichkeit für Ereignisse) 7. Materie-Ansammlung (Verklumpung) (1.Anfangs-Mechanismus von Strukturbildung mit Mastergleichung 2.Bildung von Asymmetrie 3.Gravitations-Mechanismus) 8. Emission in die Umgebung (Dunkle Energie) (Bildung von Leerräumen mit Vergrößerung durchschnittlicher freier Weglängen) 9. Erste Strukturbildung durch Materieansammlung (Dunkle Materie) (Gravitation mit Verkleinerung der freien Weglängen durch maximale Aufenthaltsdauer zweier Uratome in der Nähe zueinander.) 10. maximale Verklumpung (dichte Kugelpackung) bis hierher DUNKEL ab hier BUNT
Diskretes Standard
Modell
(älteres .pdf)
|
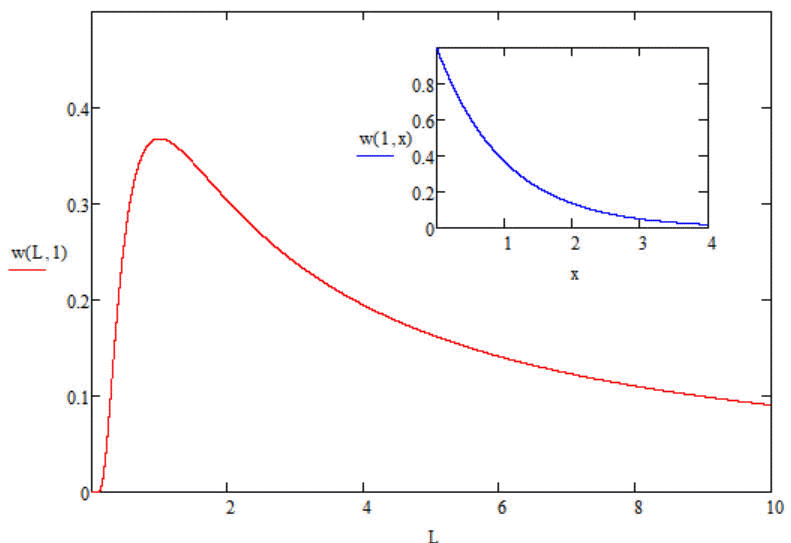
6. Verteilung der freien WeglängenAuf ähnliche Art wie durch Thermalisierung entstehen auch die freien Weglängen. Dafür kann vermutet werden, dass wegen gleicher Vorgehensweise eine ähnliche Wahrscheinlichkeitsverteilung entsteht. Mit der Abstandsfunktion (1) wird der kleinste Abstand für den nächsten Stoß ermittelt und dieser gespeichert. Nach der Sortierung ergibt sich für einen Programmdurchlauf, welcher wieder einem Zeitschritt entspricht, ein anderes Bild als in Abbildung 6 (negative Exponentialfunktion). Verwendbar zur Bestimmung von Stoßfrequenzen werden die Mittelwerte der freien Weglängen mit den Geschwindigkeitsbeträgen durch die ähnlichen Wahrscheinlichkeitsverteilungen5, weil weder die relativen Geschwindigkeitsbeträge noch die durchschnittlichen freien Weglängen L, bei Stößen verändert werden.
In dieser Formel können L oder x als Variable betrachtet werden. Im Beispiel-Diagramm (Abbildung 6) wird die andere Größe zu eins gesetzt. Ein Abstand und damit auch L = Null lässt sich nur bzgl. der Berührpunkte erreichen, mit (1) aber nicht, wenn die Mittelpunkte verwendet werden. Weil für eine lokale Stabilität Stoßfrequenzen wichtig sind, werden vorläufig nur die Mittelwerte von Geschwindigkeitsbeträgen und freien Weglängen, welche mit Magnetfeldern assoziiert werden können, betrachtet. Das geschieht jeweils im Moment der Berührung zweier Kugeln. In den Beschreibungen von quantenmechanischen Strukturen (Elementarteilchen) können auch Standardverteilungen bzw. Streuungen dieser Werte wichtig werden. Im Großen spielen die Geschwindigkeiten und freien Weglängen die entscheidende Rolle bei der Erzeugung von Strömungen, welche sich mit der Maxwellschen Elektrodynamik6 beschreiben lassen. Wegen der Gültigkeit des Superpositionsprinzips lässt sich die Anzahl der betrachteten Uratome beliebig erhöhen. Je größer diese wird, desto weniger wahrscheinlich wird allerdings eine spontane Strukturbildung. Die alleinige Betrachtung freier Weglängen ist mit einer Beschränkung auf die Eigenschaften der Masse verbunden. Diese ist als Anzahl der Uratome definiert und sollte die Ermittlung des Stärkeverhältnisses der Gravitation ermöglichen.
Abbildung 6: Wahrscheinlichkeitsdichte freier Weglängen in Abhängigkeit von deren Durchschnitt L, also bei unterschiedlicher Dichte bzw. im kleinen Bild bei einer festen durchschnittlichen freien Weglänge. Für die weiteren Überlegungen waren vorhergehende Skizzen der Ideen außerhalb dieser Formulierung des Szenarios, vor allem mit Computer Algebra Systemen hilfreich.
5Gezeigt wird das auch in [Schm 1989] auf S. 1968, (12.1.37) 6Interessant ist hier ein Vergleich mit den alten Vorstellungen, wie sie Boltzmann in seinen „Populären Schriften“ 1905 ab Seite 11 äußerte [Bol 1905].
|

Wiese, Albert Lothar: Struktur und Dynamik der Materie im Uratom-Modell, Porec/ Sarajevo 2000-2018