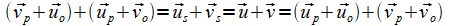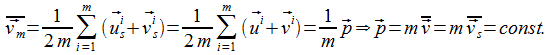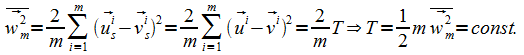Einfache diskrete Objekte zur Erweiterung des Standardmodells (DOM)

war: Stoßverhalten in einem einfachen Gas harter Kugeln (HKG) aus dem eine Erweiterung von Standardmodell und ART zum Harte Kugeln Modell (HKM) folgen soll

Inhalt (Anfang)

1. Erweiterung der Standardphysik

1.1 Wichtige Phänomene und deren Ursache

1.2 Grenzen der Beschreibung 

1.3 Motivation für ein Modell mit einfachen diskreten Objekten

2. Standardphysik im Diskrete Objekte Modell 

2.1 Formale Ansätze zur Entwicklung des DOM´s 

Axiome 

Definitionen für Erklärungsansätze 

2.2 Elementare Bewegungsgleichungen ohne Potenzial 

Stoßtransformationen 

Differenzierbarkeit 

Bewegungsgleichungen 

Wahrscheinlichkeitsfelder 

Zufallsgeneratoren als Rechenhilfen

2.3 Stöße und Erhaltungssätze 

     Impuls- und Drehimpulserhaltung

     Energieerhaltung

2.4 Entstehung von Ansammlungen (Systembildung) 

Beschreibung  der Dynamik von diskreten Objekten

Spin durch Verwirbelung

Ladung und magnetisches Moment 

Grenzen der Auffüllung 

Zufällige Systembildung 

2.5 Quantenhaftigkeit im DOM 

Eigenschaft h in der Grundmenge 

Fluktuationen 

Stoßgleichgewicht 

Erhalt der Stoßwahrscheinlichkeit 

2.6 Relativität der Raumzeit 

Energie-Impuls-Tensor im HKG 

Konstante Signalgeschwindigkeit 

Eigenschaftsänderungen bewegter Systeme 

3. Ansätze für eine diskrete Erweiterung des Standardmodells

      3.1 Substrateigenschaften

      3.2 Feldzuordnungen

      3.3 Brücke zur Standardphysik

4. Mögliches Szenario für die Weltentwicklung im DOM und daraus folgende Theorien 

4.1 Homogenes Gas 

4.2 Evolutionsbeginn 

4.3 Allgemeine Drehung 

3.4 Kugelansammlung (Gravitation) 

4.5 Jetbildung 

4.6 Elementarteilchenbildung 

4.7 Bildung von Eichbosonen  (Photonen) 

4.8 Potenzialbildung von Kugelmengen (z.B. Elektromagnetismus) 

4.9 Ausblick auf möglicherweise im DOM erklärbare Phänomene 

Literatur 

Stichwortverzeichnis 

Abbildungsverzeichnis 

Grundgrößen im HKM

2.3 Stöße und Erhaltungssätze

Erhaltungssätze werden seit langem nicht hinterfragt, weil deren Gültigkeit durch das Noether-Theorem nachgewiesen ist. Im wesentlichen wird dafür die mehrfache Differenzierbarkeit bei den Beschreibungen der zu betrachtenden Phänomene vorausgesetzt. Gerade diese ist jedoch im HKM bei elementaren Ereignissen nicht vorhanden. Was passiert aber bei den durch die Stoßtransformationen (12) und (13) beschriebenen Ereignissen?

Die betrachteten Vektoren beziehen sich auf die Stoßachse und sind mit p für parallele und mit o für orthogonale Komponenten indiziert. Durch einfaches Einsetzen folgt

Die Geschwindigkeitssumme vor einem Stoß ist gleich der Summe nach dem Stoß, unabhängig vom Stoßachsenwinkel oder dem Bahnenwinkel, den die beiden stoßenden Objekte zueinander besitzen. Am leichtesten einzusehen ist das aufgrund der Bildung der Geschwindigkeiten nach dem Stoß aus den parallelen ((8), (9)) und orthogonalen ((10), (11)) Komponenten, weil die Reihenfolge der Addition der Vektorkomponenten gleichgültig ist und die Klammern weggelassen werden können. 

Impuls- und Drehimpulserhaltung

Weil das bei allen Stößen gilt und Massen im HKM nur auf die Anzahl der Objekte zurück zu führen sein sollen, können die Objekte mit einem Index m für die Masse gekennzeichnet werden. Bei allen Stößen bleibt die Schwerpunktbewegung und somit also der Gesamtimpuls, welcher durch

beschrieben werden kann, konstant. Bewiesen wird das einfach durch Einsetzen der zueinander orthogonalen Geschwindigkeiten wie bei (27). Durch elementare Ereignisse verbundene Stoßpartner werden gemeinsam betrachtet. Die damit gebildeten Systeme sind demnach zu ihrer Umgebung offen, was weit reichende Folgen hat. Bereits bei der Bildung und dem Erhalt von Elementarteilchen kann Entropie vernichtet werden.

Die oben beschriebenen Stöße können eine beliebige Anzahl annehmen. Der Index könnte auch aus einer kontinuierlichen Indexmenge stammen und mit unserem Zeitbegriff in Verbindung gebracht werden. Bei der Menge von m beteiligten Objekten, müssen nicht alle zusammen stoßen und es kann auch Mehrfachstöße geben. Nach beliebig vielen Stößen, und das sind ja die einzigen im HKG möglichen Ereignisse, ist die Durchschnittsbewegung der beteiligten Stoßpartner unverändert, weil bei jedem einzelnen Stoß die Schwerpunktbewegung und deren Richtung mit der Geschwindigkeitssumme erhalten bleibt. Das ist die Aussage des Impulserhaltungssatzes.

Wichtig ist auch die daraus folgende Erhaltung, von in abgeschlossenen Systemen zusammen gehörender Objekte, erhaltenen Bewegungen von Stoßpartnern um ein gemeinsames Zentrum. Deshalb bleibt auch der Drehimpuls erhalten, der aus den Eigenschaften vieler Objekte in Bezug auf deren Zentrum ermittelt werden kann. Die Stabilität solcher Ansammlungen ist mit dem Spin verknüpft, der wegen seiner Wichtigkeit gesondert behandelt werden soll. Wichtigstes Ergebnis ist hier, dass bei Ansammlungen immer ein Bezug zu den Objekten der Umgebung (Relativgeschwindigkeiten) untersucht werden muss.

Energieerhaltung

Bei der Energie ist es ebenso einfach. Da vor und nach dem Stoß auch die Annäherungs- und Entfernungsgeschwindigkeits-, das sind die Relativgeschwindigkeitsbeträge, übereinstimmen, gilt dies ebenfalls für die daraus bildbaren Quadrate. Die Richtungen sind ohne Einfluss. Durch Induktionsbeweis oder wie oben mit (29) und der geeigneten Interpretation des Index s, lässt sich damit zeigen, dass auch in der Grundmenge mit Selbstwechselwirkung dafür ein Erhaltungssatz gilt, der als Energieerhaltungssatz interpretiert wird. Dabei wird aber eines der Objekte als ruhend angenommen und der Energiebegriff in Bezug auf das Ruhesystem bedarf einer Interpretation. Die Möglichkeit, Arbeit zu verrichten, steckt im Quadrat der Relativgeschwindigkeiten und ist nach Stößen unverändert:

Offensichtlich gilt aber bei einzelnen Stößen wegen des Aneinandersetzens von parallelen und orthogonalen Komponenten, dass die Summen bzw. Differenzen der Geschwindigkeitsbeträge im Allgemeinen unterschiedlich von denen vor dem Stoß sind. Nach dem Satz von Pythagoras wird das verständlich, weil beim orthogonalen Stoß beispielsweise eines der beiden Objekte im betrachteten Koordinatensystem zum Stillstand gebracht werden kann, während das andere den Geschwindigkeitsbetrag der Hypotenuse erhält. Dieser scheinbare Widerspruch führt dazu, dass bei den elementaren Ereignissen lokal sehr wohl Energie relativ zu anderen Objekten als dem Stoßpartner erzeugt oder vernichtet werden kann. Durch diese Veränderungen werden Systembildungen erst denkbar, wenn sich die unterschiedlichen Komponenten massenweise in verschiedenen, zusammen­gehörenden Teilmengen der Grundmenge, d.h. in Systemen befinden.

Weil Massen mit der Anzahl elementarer Objekte verknüpft sind, ist intuitiv eine Ansammlung von solchen Objekten, die über längere Zeit stabil bleibt mit dem Begriff eines Systems verbunden, das als Elementarteilchen bezeichnet werden kann. Das Ansammeln kann nur erfolgen, wenn massenweise in dem betrachteten Gebiet kleinere Geschwindigkeitsvektoren (zumindest vom Zentrum weg) erzeugt werden, die zu einem Zurückbleiben von Objekten in diesem Bereich führen, was bei häufigen seitlichen Stößen auftritt. Die Auffüllbarkeitsgrenze des Gebiets kann nun in Verbindung mit Drehimpuls- und Energieerhaltung zur Stabilität des betrachteten Systems führen. Nötig ist dafür aber eine Entropieabnahme. Im derzeitigen Stand der Entwicklung des DOM´s ist das noch nicht zu beweisen, weiter unten soll aber noch darauf eingegangen werden.

Gegenteil davon ist die bei frontaleren Stößen zu beobachtende Zunahme der Geschwindigkeits-Betrags-Summen. Diese erzeugen verstärkte Dichtefluktuationen, weil die Abstände von ursprünglichen Systemzentren nach bestimmten Zeitintervallen größer werden. Das ist auch die Ursache der Thermalisierung, bei der die Maxwell-Boltzmannsche Geschwindigkeitsverteilung erzeugt wird. Damit lässt sich die Entropiezunahme erklären. Entropie wird deshalb hier als Maß der Systembildung betrachtet, in das die Teilchenzahldichte der elementaren Objekte eingeht.

Elementare Eigenschaften der Grundmenge sind die Anwesenheit und die Bewegung der kleinsten Objekte (hier Kugeln) an Raum-Zeit-Punkten. Wegen der notwendigen Wahrscheinlichkeitsbetrachtung wird angenommen, dass diese durch Dichte- und Geschwindigkeitsverteilungen genügend genau beschrieben werden. Welchen Einfluss haben nun die möglichen Vektorwinkel und vielleicht die Stoßachsenwinkel auf diese Wahrscheinlichkeitsverteilungen? Dazu muss die Betrachtung im ortslosen Gas verlassen werden.

Die Geschwindigkeits-Normalverteilung und auch die lokale Anzahldichte verändern sich bei Stößen normalerweise lokal, also zumindest in der näheren Umgebung. Kugelmengenflüsse mit schmalerer oder breiterer Geschwindigkeitsverteilung und von der Durchschnittsgeschwindigkeit abweichendem Erwartungswert sind möglich. Die Stoßzahl (Stoßfrequenz => Stoßhäufigkeit)

bestimmt den erwarteten Objekte-Fluss durch eine interessierende Fläche. Deshalb ist es notwendig, einen Zusammenhang mit den vorn betrachteten Wahrscheinlichkeiten für das Auftreten von Vektor- und Stoßachsenwinkeln herzustellen. Bei einer entsprechenden Vektordarstellung lassen sich möglicherweise die Erwartungswerte direkt einsetzen.

Interessant werden hier Überlegungen, dass die Stoßhäufigkeit von der erwarteten Aufenthaltszeit in einem bestimmten Raumbereich abhängt. Diese ist zwar umgekehrt proportional zur (Relativ-)Geschwindigkeit der betrachteten Kugeln, die Stoßzahl Z erhöht sich aber proportional zu dieser. Die freie Weglänge ist dabei von der Geschwindigkeit unabhängig. Das sieht man leicht durch auflösen von (30) nach L. Für den Aufbau der Welt aus existierend angenommenen kleinsten Objekten wichtige Stoßfälle ergeben die elementaren Eigenschaften einer Ansammlung und seien deshalb in Stichworten aufgezählt:

1. Der Annäherungs-Geschwindigkeits-Betrag ist nach einem Stoß gleich dem Entfernungs-Geschwindigkeits-Betrag, d.h. der Relativgeschwindigkeits-Betrag wird bei Stößen nicht verändert. => Impulserhaltung.

2. Der Relativgeschwindigkeits-Betrag und auch dessen Quadrat ändern sich bei Stößen nicht. => Energieerhaltung.

3. Die Geschwindigkeits-Betrags-Summe ist nach frontalen Stößen meistens größer als vorher.=> Ein Hinweis auf Entropiezunahme.

4. Die Geschwindigkeits-Betrags-Differenz ist nach frontalen Stößen meistens kleiner. Bei Frontalstößen passen sich die Geschwindigkeitsbeträge an. => Konstante Durchschnittsgeschwindigkeit mit schmaler Streuung.

5. Bei Querstößen, also häufigen Fällen im homogenen Gas, ergibt sich oft eine Geschwindigkeits-Betrags-Abnahme und deshalb Anzahldichte-Zunahme. => möglicherweise Systembildung, also ein Hinweis auf Entropieabnahme.

6. Nach einem Stoß, bei dem die Geschwindigkeits-Betrags-Summe kleiner wird, nimmt die Anzahldichte in der Stoßumgebung zu, weil nach einem festen Zeitintervall die Entfernungssumme vom Stoßpunkt kleiner ist als im gleichen Zeitintervall vor dem Stoß bzw. wenn die Kugeln nahe aneinander vorbei fliegen würden.

7. Trotz separater Dichte- und Durchschnittsgeschwindigkeits-Änderungen gilt die Liouville-Gleichung (vgl. auch 2.5 Quantenhaftigkeit im HKM), d.h. Die Phasenraumdichte ändert sich nicht.

Die Anzahldichte-Zunahme und damit selbständige Materieansammlung in einer chaotischen Menge stoßender Kugeln stehen im Widerspruch zur landläufigen Meinung und es ist unklar, ob darüber schon berichtet wurde. Die Suche nach einem Beweis dafür ist eine der aktuellen Hauptaufgaben (vgl. .../Beweise, Geschwindigkeitsanpassung,...).

Die Erkenntnisse bis hierher wurden noch ohne detaillierte Untersuchungen des Einflusses unterschiedlicher Dichte auf das Vorkommen verschiedener Winkel gewonnen. Als wichtigste Eigenschaft im betrachteten HKG muss deren Einfluss aber systematisch untersucht werden. Derzeitige Anfangsüberlegungen zu den Winkelwahrscheinlichkeiten und frühere Vermutungen über häufige Frontalstöße müssen demnach systematisch erweitert und verbessert werden. Wichtig ist dabei vor allem die Ermittlung von Grenzwerten bei vielen zu untersuchenden Stößen. Offensichtlich ist das Auftreten von gegenseitig bedingten Wechseln zwischen Dichte und Schnelle beim Schall in tatsächlich existierenden Gasen, welche durch harte Kugeln modelliert werden können. Diese werden durch Stöße erzeugt und beeinflussen die Stoßwahrscheinlichkeiten (Stoßfrequenzen) in ihrer Umgebung. Eine Raumzeitverzerrung durch die Selbstwechselwirkung, also Stöße der elementaren Feldobjekte, ist demnach anschaulich vorstellbar durch die mit jeder Bewegung in der Umgebung verbundene Änderung der Auftreffwahrscheinlichkeit.