 |
 |
|
 |
 |
|
 |
||
Einfache diskrete Objekte zur Erweiterung des Standardmodells (DOM)
war: Stoßverhalten in einem einfachen Gas harter Kugeln (HKG) aus dem eine Erweiterung von Standardmodell und ART zum Harte Kugeln Modell (HKM) folgen soll
Inhalt (Anfang)
1. Erweiterung der Standardphysik
1.1 Wichtige Phänomene und deren Ursache
1.3 Motivation für ein Modell mit einfachen diskreten Objekten
2. Standardphysik im Diskrete Objekte Modell
2.1 Formale Ansätze zur Entwicklung des DOM´s
Definitionen für Erklärungsansätze
2.2 Elementare Bewegungsgleichungen ohne Potenzial
Zufallsgeneratoren als Rechenhilfen
Impuls- und Drehimpulserhaltung
2.4 Entstehung von Ansammlungen (Systembildung)
Beschreibung der Dynamik von diskreten Objekten
Ladung und magnetisches Moment
Eigenschaft h in der Grundmenge
Erhalt der Stoßwahrscheinlichkeit
Konstante Signalgeschwindigkeit
Eigenschaftsänderungen bewegter Systeme
3. Ansätze für eine diskrete Erweiterung des Standardmodells
4. Mögliches Szenario für die Weltentwicklung im DOM und daraus folgende Theorien
3.4 Kugelansammlung (Gravitation)
4.7 Bildung von Eichbosonen (Photonen)
4.8 Potenzialbildung von Kugelmengen (z.B. Elektromagnetismus)
4.9 Ausblick auf möglicherweise im DOM erklärbare Phänomene
2.4 Entstehung von Ansammlungen (Systembildung)
Beschreibung der Dynamik von diskreten Objekten
Bewegte Kugeln ändern ihre Orte geradlinig gleichförmig bis zu Stößen. Für die mathematische Beschreibung können die Definitionen aus 2.1 verwendet werden. Das klingt noch sehr einfach, handelt es sich doch um einfache, geometrisch erklärbare, physikalische Vorgänge. Konkrete Kugelorte und Geschwindigkeiten sind aber nicht bekannt und sollten für Simulationen des möglichen Verhaltens sehr große Teilchenzahlen umfassen. Aus den bekannten Simulationsmethoden (vgl. z.B. [S 06]) der physikalischen Literatur erscheinen nur einige Ideen nutzbar, weil für Geschwindigkeitsänderungen i.A. Potenziale verwendet werden, hier jedoch zusätzlich und als elementare Ursache die Stoßtransformationen.
Weil nun die sehr große Zahl zu betrachtender Kugeln weit oberhalb der mit Computern direkt numerisch behandelbaren liegt, andererseits aber tatsächliche Ortsänderungen wegen möglicher Fluktuationen untersucht werden sollen, soll hier ein hybrides, an Monte-Carlo-Methoden angelehntes Verfahren verwendet werden. Lattice-Boltzmann-Simulationen verwenden räumliche und zeitliche Intervalle (Gitter). Die Schwierigkeit wird offensichtlich, wenn man sich vor Augen hält, dass ja keine Kraft bzw. kein Potenzial unser HKG zusammen hält, aber trotzdem starke Inhomogenitäten betrachtet werden sollen. Ein Ansatz ergibt sich lediglich dadurch, dass möglicherweise über längere Zeit stabile Systeme ein gewisses Stoßgleichgewicht gegenüber ihrer Umgebung besitzen sollten. Das impliziert aber beim Generieren von zufälligen Werten, welche in die Stoßtransformationen eingehen, die notwendige Kenntnis komplizierter Wahrscheinlichkeitsverteilungen für die Zufallsgeneratoren, die möglichst in sehr kleinen Zeitintervallen an neue Situationen in der Umgebung angepasst werden sollten. Das erfordert Kompromisse bei der tatsächlichen Realisierung, auch mit den leistungsfähigsten Computern.
Für jede zu beschreibende Kugel wird ein Startpunkt im dreidimensionalen Raum zu einem bestimmten Zeitpunkt benötigt. Für diese kann anfangs eine homogene Gleichverteilung angenommen werden, die mit Hilfe einer Teilchenzahldichte realisiert wird. Auch die Geschwindigkeiten lassen anfänglich willkürliche Werte zu, wobei alle Richtungen gleich wahrscheinlich sein sollten. Eine damit beginnende Simulation kann deshalb sogar ortslos beginnen und ergibt nach genügend Stößen durch Thermalisierung die Maxwell-Boltzmann-Verteilung für die Geschwindigkeiten.
Wie ändern sich aber die zugrunde zu legenden Wahrscheinlichkeitsverteilungen bei lokalen Inhomogenitäten? An einem betrachteten Raum-Zeit-Punkt (vierdimensional aber nicht relativistisch) muss einerseits die Geschwindigkeit einer Probekugel bekannt sein, welche zufällig mit einer aus der Umgebung zusammen stoßen soll. Für jede Raumrichtung der Umgebung sollte nun je eine Wahrscheinlichkeitsverteilung für die Geschwindigkeit auf die Probekugel zu und eine Wahrscheinlichkeitsverteilung für die Teilchenzahldichte bekannt sein. Beide bestimmen gemeinsam die erwartete Stoßfrequenz aus der entsprechenden Richtung, also die schon erwähnte Stoßfrequenzraumwinkeldichte (siehe Brendel-stoss.pdf S. 6 ff). Nur Kugeln die sich im Stoßkegel auf die Probekugel zu bewegen, können stoßen und sollen berücksichtigt werden. Deshalb soll die gewöhnliche Anzahldichte um eine Abhängigkeit von der Bewegungsrichtung ergänzt werden. Zur Beschreibung sind so pro Richtung wenigstens zwei bzw. vier reelle Parameter (Erwartungswert und Varianz) einer angepassten Normalverteilung für Geschwindigkeit und Teilchenzahldichte erforderlich. Im allgemeinen Fall können die Verteilungen aber auch komplizierte Funktionen mit beliebig vielen Maxima sein. Diese kann man sich vorstellen, als ob sie um den Raum-Punkt zu einem bestimmten Zeitpunkt vier dreidimensionale geschlossene Flächen (Hüllen) bilden. Mit vier Parametern sollten sich beispielsweise richtungsabhängige Stoßfrequenzen und mit Hilfe der Zufallsgeneratoren auch konkrete Realisierungen für Simulationen ermitteln lassen. Im Gegensatz zur ortslosen Simulation brauchen für die Stoßachsen keine zufälligen Winkel mit Zufallsgeneratoren ermittelt zu werden, weil die Geometrie des Auftreffpunktes mit den Startpunkten und der geradlinigen Bewegung der Kugeln bestimmt ist.
Spin durch Verwirbelung
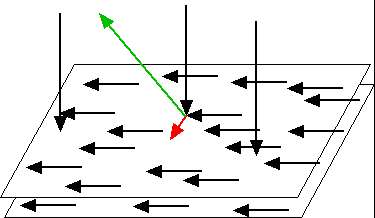
Schon vorn wurde vermutet, dass bei Stößen mit abnehmender Geschwindigkeitsbetrags-Summe eine Ansammlung erfolgen kann. Das Gleiche geschieht auch, wenn beispielsweise bei vielen Stößen in einem Gebiet bevorzugt ein Stoßpartner in einer Richtung fliegt und durchschnittlich einen kleineren Geschwindigkeitsbetrag als der andere Stoßpartner erhält (Abbildung 9).
Bevorzugte Bewegung in einer Richtung könnte einerseits von den auftretenden Flugwinkeln beeinflusst werden, andererseits von den Stoßachsenwinkeln. Normalerweise sollten dabei aus der Umgebung eines Raumpunktes (isotropisch) alle Richtungen gleich betrachtet werden. Weil die Isotropie zum Erhalt von Drehimpulsen führt, ist auch der Gedanke nahe liegend, dass stabile Ansammlungen, also Systeme, mit Wirbeln zu erklären sind. Über die elementaren Eigenschaften des Gases mit den angenommenen kleinsten Objekten ist allerdings hier noch nichts bekannt. Es wird aber vorausgesetzt, dass es zumindest stückweise gerade Bahnen dieser Objekte in den Ansammlungen geben muss. Ist nun zufällig, wenn auch mit geringer Wahrscheinlichkeit, eine höhere Dichte als im normalen Raum der Umgebung, entstanden, löst sich diese normalerweise wegen der in Richtung kleinerer Dichte geringeren Stoßfrequenz (bzw. Stoßwahrscheinlichkeit) und der deshalb größeren erwarteten freien Weglänge schnell wieder auf. Anders kann das eventuell sein, wenn die Bewegung eines der beiden Stoßpartner mit kleinerer (bzw. der systeminternen) Geschwindigkeit in die zulässige Richtung einer Wirbeldrehung erfolgt. Welcher der beiden Stoßpartner dabei zum ursprünglichen Wirbel (bzw. Wirbelbeginn) gehört, ist unerheblich. Es kommt nur darauf an, dass einer der beiden nach dem Stoß die Wirbeleigenschaft verstärkt. Das kann bei gewissen vorkommenden Stoßachsen- und Vektorwinkeln der Fall sein. Leicht zu zeigen ist auch (z.B. Abbildung 9), dass es solche Stöße gibt. Nachgewiesen werden muss allerdings, dass es HKG-Eigenschaften geben kann, die das massenweise Vorkommen solcher Stöße ermöglichen. Das ist eine Hauptaufgabedes zu entwickelnden DOM´s. Vor allem bei einer starken Energieansammlung kommen wegen der erhöhten Stoßfrequenz viele Stoßpaare vor, bei denen durch eine bevorzugte massenweise Bewegung gegenüber dem umgebenden Raum ein häufiges Zusammenfinden von langsameren oder schnelleren Kugeln erfolgen kann, was zur Paarbildung von Wirbeln führen könnte.
Bei der näheren Betrachtung kann ein Gebiet heraus gegriffen werden, in dem eine solche Ansammlung zufällig entstand, wo also eine große Anzahl von Kugeln in bevorzugten Richtungen fliegt. Deren gerade Bahnen können anfangs ungefähr die Durchschnittsgeschwindigkeit 1 besitzen. Zu Stößen dieser Teilchen untereinander kommt es dann nur durch geringe Geschwindigkeitsbetrags-Unterschiede. Die freie Weglänge ist nach (30) von der Geschwindigkeit unabhängig. Zur verhinderung von Auflösung einer Ansammlung ist wichtig, dass durch Stöße, bei denen ein Stoßpartner Geschwindigkeitsbetrag verliert, dessen Flug im Durchschnitt in Richtung des Dichtezentrums erfolgt. Zur Wirbelbildung kommen vor allem einseitige Stöße infrage, aber aus einer Umgebung mit durchschnittlichen Eigenschaften, dem Normalraum. Der besser zu den Systemeigenschaften passende Stoßpartner wird nach dem Stoß zum System gehörig betrachtet. Die andere Seite kann vom Wirbel selbst abgeschirmt werden, falls entweder die erwartete freie Weglänge nur einen Stoß von außen erwarten lässt oder Kugelströmungen aus dem Ansammlungsgebiet das erwarten lassen.
Hier wird ein Erhalt von solchen Eigenschaften über einen längeren Zeitraum noch nicht betrachtet, weil das nur im Zusammenhang mit dem Verhalten in großen Raumgebieten möglich ist. Die dazu erforderliche Quantenhaftigkeit wird weiter unten behandelt, weil die Gültigkeit der Größe h in allen Naturgesetzen vorausgesetzt, aber bisher nicht ursächlich erklärt wird. Das Eingehen des Faktors 2π in ℏ drückt einen Wiederholungsfaktor nach einer vollen Drehung in Wellengleichungen aus, der aber seine volle Bedeutung erst durch die immer und überall gültige Quantenhaftigkeit erhält, welche weiter unten gezeigt wird (2.5).
Mathematisch reichen hier die zur Beschreibung einer Stoßfrequenz
sich anbietenden komplexen Zahlen nicht aus, weil die zu
beschreibenden Feldgrößen der Selbstwechselwirkung durch Stöße
winkelabhängig sind. Die klassischen zur Verfügung stehenden
Hilfsmittel mit vier reellen Parametern zur Drehimpulsbeschreibung
reichen hier allerdings noch aus. Für die Stoßachsenwinkel kann das
Vorkommen paralleler Flugbahnen zu den durch die
Stoßfrequenzraumwinkeldichte bestimmten Flugwinkeln angenommen
werden. Dann reichen zwei zusätzliche Parameter zur Beschreibung von
deren Erwartungswerten, welche alle möglichen Richtungen
beschreiben. Mit diesen (Skalarprodukt von Winkeln und Drehimpuls,![]() , vgl. [B 86] S.26) kann der globale komplexe
Phasenfaktor eia gebildet werden, mit welchem die Psi-Funktion zur
Beschreibung des Spins
multipliziert wird. Diese zur Beschreibung von Elementarteilchen zu
verwendende Funktion ist hier zwar noch nicht definiert, soll aber
wie in der Quantenmechanik üblich, von einer nur in der näheren
Umgebung des betrachteten Raum-Zeit-Punktes endliche Impulswerte
enthaltenden Gleichung beschrieben werden (Schrödinger-Gleichung).
Das Entstehen fester, also quantisierter Werte zur Bildung stabiler
Elementarteilchen muss allerdings noch nachgewiesen werden. Dafür
sollten die möglichen halbzahligen Spin-Quantenzahlen verständlich
werden. Bei Teilchen ohne Spin (Spin 0) ist keine Verschiebung des
Vektorwinkelerwartungswertes zu vermuten, bei Teilchen mit Spin ½
gibt es möglicherweise gleich viele Stöße mit Partnern aus dem
System wie mit solchen aus der Umgebung und bei Teilchen mit Spin 1
dann wohl nur Stöße mit Partnern aus der Umgebung.
, vgl. [B 86] S.26) kann der globale komplexe
Phasenfaktor eia gebildet werden, mit welchem die Psi-Funktion zur
Beschreibung des Spins
multipliziert wird. Diese zur Beschreibung von Elementarteilchen zu
verwendende Funktion ist hier zwar noch nicht definiert, soll aber
wie in der Quantenmechanik üblich, von einer nur in der näheren
Umgebung des betrachteten Raum-Zeit-Punktes endliche Impulswerte
enthaltenden Gleichung beschrieben werden (Schrödinger-Gleichung).
Das Entstehen fester, also quantisierter Werte zur Bildung stabiler
Elementarteilchen muss allerdings noch nachgewiesen werden. Dafür
sollten die möglichen halbzahligen Spin-Quantenzahlen verständlich
werden. Bei Teilchen ohne Spin (Spin 0) ist keine Verschiebung des
Vektorwinkelerwartungswertes zu vermuten, bei Teilchen mit Spin ½
gibt es möglicherweise gleich viele Stöße mit Partnern aus dem
System wie mit solchen aus der Umgebung und bei Teilchen mit Spin 1
dann wohl nur Stöße mit Partnern aus der Umgebung.
Über diese Betrachtungen hinaus gehen Überlegungen, ob großräumig um verwirbelte Materieansammlungen herum durch geringfügige Verschiebung der Erwartungswerte vorkommender Winkel eine allgemeine Verwirbelung entstehen könnte. Diesen könnten sogar Elementarteilchen ohne Ladung zugeordnet werden, obwohl deren notwendige Quantisierung noch nicht behandelt wurde. Spekulativ könnten solche Teilchen als ruhende Neutrinos zur Bildung dunkler Materie interpretiert werden.
Ladung und magnetisches Moment
Schon vorn wurde den Bewegungen der kleinsten Objekte eine elektrische Feldkomponente und dem durch die freien Weglängen charakterisierten Fluss bzw. Transport von kleinsten Objekten eine Magnetfeldkomponente zugeordnet.
Zur Überprüfung, ob in Systemen harter Kugeln, durchschnittlich Geschwindigkeitsbeträge erzeugt werden können, die innen niedrigere Durchschnittswerte und außen entsprechend höhere erzeugen oder umgekehrt, kann der Zeitfaktor und die räumliche Verteilung vernachlässigt werden, wenn man ohne diese auf die bei den Stößen durchschnittlich vorkommenden Winkel schließen kann. Diese können dann in einer Simulation vieler Stöße in einem ortslosen Gas, ähnlich der zur Thermalisierung, verwendet werden. Dabei lässt sich möglicherweise unter vorsichtiger Betrachtung und mit einer noch nicht untermauerte (mit dem Spin ½ könnte eine Asymmetrie der Stoßfrequenzraumwinkeldichte verbunden sein, welche einen festen Mittelwert von ß erzeugt) Wahrscheinlichkeitsdichte für den Bahnenwinkel ß, nach vielen Stößen eine Annäherung der durchschnittlichen Geschwindigkeitsbetragsänderung an die Feinstrukturkonstante zeigen.
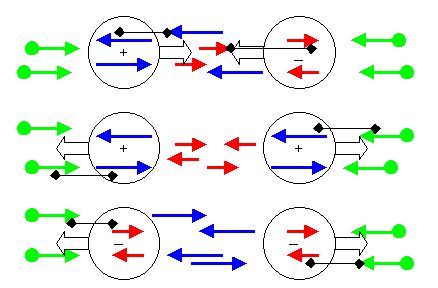
Abbildung 10: Potenzialbildung durch Mischung
Die elektroschwache Wechselwirkung ist hier in der Form von mischenden Geschwindigkeitsvektoren dargestellt. Obwohl diese eigentlich nur reine elektrische Felder (virtuelle Photonen) beschreiben, kann der Mechanismus auch auf die Kugelmengen-Flüsse (Anzahldichte) des magnetischen Feldes und beispielsweise systeminterne Axialvektorströme der schwachen Wechselwirkung angewandt werden. Allen diesen superponierbaren Wechselwirkungen ist im DOM gemeinsam, dass ja die aus anderen Systemen kommenden kleinsten Objekte nicht von systeminternen unterschieden werden können. Eine Verlagerung des Systemes erfolgt immer dorthin, wo die zu den systeminneren Eigenschaften ähnlichste Umgebung erwartet wird. Das ist hier durch die schwarzen Verbindungslinien angedeutet. Über die Beschreibungsmöglichkeiten mit dem Coulombschen Gesetz und bei bewegten Ladungen mit Hilfe der Maxwellgleichungen gibt es genügend Literatur, so dass hier nicht weiter darauf eingegangen wird. Deutlich wird aber, dass die Existenz der Grundmenge, also des Gases diskreter Objekte, durchaus mit der Existenz verschiedener Felder in Zusammenhang gebracht werden kann.
Zusammen mit den im vorhergehenden Abschnitt betrachteten Verwirbelungen, welche unter festen Eigenschaften des umgebenden Raumes Quantenhaftigkeit zeigen, sind auch Flüsse, also Materietransporte mit den erzeugten Geschwindigkeitsvektoren verbunden. Diesen wurden vorn Eigenschaften von Magnetfeldern zugeordnet, so dass diese Eigenschaft von kleinen Kugelansammlungen als magnetisches Moment bezeichnet werden kann.
Grenzen der Auffüllung
Bei harten Kugeln kann es keine zwei gleichzeitigen Stöße geben. Keine zwei Objekte (Kugeln) können sich ein beliebiges endliches Zeitintervall lang berühren, so dass die Stoßreihenfolge unterschieden und deshalb geordnet werden kann. Ruhende Kugeln kann es im HKM nicht geben. Durch einen Außenstoß wird meistens ein dabei erzeugter Geschwindigkeitsvektor ins Systeminnere übertragen und einer bleibt nach dem Stoß außerhalb, weil die Ebene orthogonal zur Verbindung des Stoßpunkts mit dem Mittelpunkt des Systems durchschnittlich von einem Stoßpartner so geschnitten werden kann, dass der Durchschnittswert der Drehung des Systems erhalten bleibt. Das muss allerdings bewiesen werden.
Ist das Systeminnere dichter als die Umgebung, wäre für die innere Kugel viel früher der nächste Stoß zu erwarten, als für die äußere, falls die Bewegung dort ungeordnet ist. Herrscht eine entsprechende niedrige Durchschnittsgeschwindigkeit vor, kann das erwartete Zeitintervall allerdings genau so groß sein, wie bei der äußeren Kugel. Bewegen sich die Kugeln chaotisch in einer Schar (Schwarm, beschreibbar durch Wahrscheinlichkeitsstromdichte) mit überlagerter gemeinsamer Schargeschwindigkeit, kann es sein, dass der betrachtete Außenstoß sich ungefähr orthogonal nach innen in die Schar fortpflanzt. Zum umgebenden Raum kann trotz höherer Durchschnittsgeschwindigkeit ein Stoßgleichgewicht herrschen. Die möglicherweise systembildende überlagerte annähernd orthogonale Geschwindigkeit kann einen von beiden Durchschnittsgeschwindigkeiten abweichenden dritten Geschwindigkeitsbetrag besitzen und die in die Umgebung entweichende einen vierten. Diese Geschwindigkeitsvektoren können als elektromagnetisches Feld interpretiert werden.
Intuitiv erscheint es bei einem normalen Außenstoß auf eine Ansammlung logisch, dass die nach innen weiter gegebene Geschwindigkeit bei der Übertragung auf benachbarte Kugeln sich immer mehr der Durchschnittsgeschwindigkeit anpasst. Ist diese kleiner als die äußere Durchschnittsgeschwindigkeit, müsste diese also ebenfalls kleiner werden. Es bleiben dann aber Geschwindigkeitsüberschüsse auf dem jeweiligen Stoßpartner, die sich auch wieder auf andere Kugeln übertragen. Eine Kugel, die beim Billard auf die ruhende Ansammlung gestoßen wird, lässt alle auseinander fliegen. Gegenteilige Beobachtungen gibt es nicht, ob diese aber wirklich auszuschließen sind, muss mathematisch nachgewiesen werden.
Um etwas systematischer an das Problem möglicher Systembildung heran zu gehen, soll eine Schar von Kugeln betrachtet werden, die sich orthogonal zu einem gedachten Systemmittelpunkt bewegt. Nach einem Außenstoß kann die Bewegung nach innen von dieser Kugel so lange ungestört geradlinig fortgesetzt werden, bis ein weiterer Außenstoß erfolgt. Es kann aber auch sein, dass vorher ein innerer, also sekundärer Stoß stattfindet, oder zwei, drei, ..., jeweils natürlich im Durchschnitt der betrachteten Kugeln.
Weiter gehend sollen N untersuchte Kugeln beispielsweise, stellvertretend für diese, Nm in einem systeminternen Gebiet beschreiben, das kugelförmig sein soll. In der Umgebung von Stoßpunkten soll wegen einer vermuteten großen Teilchenzahl und wegen deren zwar unbekannter, aber vorhandener, Ausdehnung und damit vorhandener Dichte, davon ausgegangen werden, dass das betrachtete Gebiet zwar annähernd kugelförmig ist, ein kleiner Teil der betrachteten Oberfläche aber eben, d.h. ohne Krümmung.
Beim einfachen Stoß kann entschieden werden, dass der erste Stoßpartner aus der beobachteten Menge kommt und der zweite Stoßpartner entweder aus dieser oder von außerhalb. Wegen des Stoßgleichgewichts mit der Umgebung sollte jeder zweite Stoß im Randbereich einer mit äußerem bzw. innerem Partner sein. Darüber hinaus weiter innen stattfindende Stöße werden vernachlässigt, weil Geschwindigkeits-Zu- und -Abnahmen sich in der Bilanz nicht auswirken. Welcher der Stoßpartner sich dann nach dem Stoß weiterhin im betrachteten Bereich, also System bewegt, wird durch seine Bewegungsrichtung gegenüber der betrachteten Fläche bestimmt. Diese ist durch den vorhergehenden Außenstoß festgelegt, wenn vereinfachend unterstellt wird, dass der Einfluss von Innenstößen vernachlässigt werden kann. Alle neuen Geschwindigkeiten werden gespeichert und mit diesen kann ein neuer Mittelwert bestimmt werden.
Falls gezeigt werden kann, dass nach vielen Stößen die systeminterne Durchschnittsgeschwindigkeit kleiner wird als die äußere, ist ein Teil des Beweises der Möglichkeit von Systembildung, geschafft. Möglich sein sollte das immer noch im ortslosen Gas und soll deshalb in verschiedenen Simulationen versucht werden. Mit den neuen Mittelwerten (Geschwindigkeitsbetrag und Richtung) kann der Versuch wiederholt werden. Dabei ist es auch denkbar auf zwei verschiedene Arten das Verhalten weiter zu untersuchen:
a) mit Außenstößen aus der unveränderten Umgebung
b) mit zufälligen Außenstößen mit den neuen Mittelwerten.
Falls ähnliche Geschwindigkeitsänderungen bei b) eintreten, könnte ein immer kleinerer Geschwindigkeitsbetrag erreicht werden. Das impliziert Dichtezunahme und Aufsammlung sehr vieler Kugeln aus der Umgebung. Es sollte eine bisher in Gasen nicht beobachtete Abnahme von Entropie beweisen.
Die Arbeit an dieser Problematik, das heißt die Untersuchung von zufälligen Stößen (erste Ansätze) erfolgt derzeit parallel zu den Formulierungsversuchen dieser Zusammenfassung und die Ergebnisse sind unter http://www.uratom.de/Beweise/Beweise.html zur Diskussion gestellt. Letztes berücksichtigtes Ergebnis und zugleich Beispiel für das Geschehen in einem einfachen ortslosen Gas harter Kugeln ist dessen Thermalisierung (.pdf). Selbst hier gleichen sich die Geschwindigkeiten bis zum Stoßgleichgewicht an die Umgebung an. In einer abgewandelten Monte-Carlo-Simulation werden dabei durch das Verfahren mit impliziten Funktionen für Wahrscheinlichkeitsfunktionen, die sonst schwer oder nicht lösbar sind, Geschwindigkeitsbeträge generiert. In jeder homogenen isotropen Umgebung passt sich hierbei die Geschwindigkeitsverteilung der Maxwell-Boltzmann-Verteilung an. Die Wahrscheinlichkeitsfunktionen werden dabei aus den gespeicherten Daten ermittelt, so dass auch inhomogene nicht isotrope Ansammlungen betrachtet werden können. Eine Erklärung des Paradoxons von Feldenergieänderungen ist durch die Thermalisierung im Vakuum offensichtlich.
N Kugeln mit Berücksichtigung der Raumzeit (4 Dimensionen) und Geschwindigkeit (EW, Varianz) sowie Dichte (EW, Varianz) könnten über einen längeren Zeitraum in einer rein statistischen aber unveränderbaren Umgebung simuliert werden. Falls der Nachweis der Möglichkeit von Entropieabnahme gelingt, besteht eine Hoffnung, auch Systembildungen in solch einer Umgebung zeigen zu können. Das ist allerdings eine noch viel größere Aufgabe, weil ja die Bildung von Elementarteilchen gezeigt werden sollte. Einige Grundgedanken dazu sind:
Zufällige Stöße können im betrachteten System und von außen pro Kugel gleich häufig sein. Vereinfacht können dann interne und externe Stöße abwechselnd betrachtet werden. Ein zufälliger Stoß kann durch 4 + 8 zufällig ermittelte Zahlen beschrieben werden. Die Zufallsgeneratoren erhalten anzupassende Erwartungswerte und Varianzen von Geschwindigkeit und Dichte. Die Anpassung erfolgt beispielsweise nach durchschnittlich einmaligem Stoß und Ermittlung der zurückgelegten Entfernungen. Ein erhoffter Nachweis der Ansammlung kann dann durch Überprüfung der Abstände der Systemkugeln vom gedachten Systemmittelpunkt nach gleich großen Zeitintervallen erfolgen.
Vor einer Verwendung der Beschreibungsmöglichkeiten eines quantenmechanischen Objektes, z.B. durch die Schrödingergleichung, ist erst einmal die wichtigste in diese einfließende Eigenschaft, also das Vorkommen der Größe h, als natürliche Eigenschaft des HKG zu zeigen. Die Wellenfunktion hat im wesentlichen nur in einer kleinen Umgebung von Null abweichende Werte des Impulses. Das wird meist wahrscheinlichkeitstheoretisch interpretiert, kann und soll hier aber als tatsächliche kleine „Wolke“ von harten Kugeln um den Schwerpunkt interpretiert werden. Mit dieser Idee sollten sich durch einen Zufallsgenerator einzelne harte Kugeln für eine Simulation generieren lassen. Das Hauptinteresse liegt aber im Nachweis von Stabilität von Spin ½ Teilchen. Für die Beschreibung des Elektrons sind Spinoren,... in der zu verwendenden Diracgleichung erforderlich. Diese ist eine relativistische Gleichung und verlangt deshalb auch noch den Nachweis der konstanten Lichtgeschwindigkeit im HKG. Für beide Nachweise soll hier, was eigentlich nicht korrekt ist, die Existenz von stabilen Systemen angenommen werden, obwohl diese hier noch nicht bewiesen ist.
WEITER HKM.pdf in Deutsch